
- 數位電子教程
- 數位電子 - 首頁
- 數位電子基礎
- 數字系統型別
- 訊號型別
- 邏輯電平與脈衝波形
- 數字系統元件
- 數字邏輯運算
- 數字系統優勢
- 數制
- 數制
- 二進位制數表示
- 二進位制運算
- 有符號二進位制運算
- 八進位制運算
- 十六進位制運算
- 補碼運算
- 進位制轉換
- 進位制轉換
- 二進位制轉十進位制
- 十進位制轉二進位制
- 二進位制轉八進位制
- 八進位制轉二進位制
- 八進位制轉十進位制
- 十進位制轉八進位制
- 十六進位制轉二進位制
- 二進位制轉十六進位制
- 十六進位制轉十進位制
- 十進位制轉十六進位制
- 八進位制轉十六進位制
- 十六進位制轉八進位制
- 二進位制編碼
- 二進位制編碼
- 8421 BCD碼
- 餘3碼
- 格雷碼
- ASCII碼
- EBCDIC碼
- 編碼轉換
- 錯誤檢測與糾錯碼
- 邏輯閘
- 邏輯閘
- 與門
- 或門
- 非門
- 通用門
- 異或門
- 異或非門
- CMOS邏輯閘
- 使用二極體電阻邏輯實現或門
- 與門與或門
- 雙電平邏輯實現
- 閾值邏輯
- 布林代數
- 布林代數
- 布林代數定律
- 布林函式
- 德摩根定理
- SOP和POS形式
- POS到標準POS形式
- 最小化技術
- 卡諾圖最小化
- 三變數卡諾圖
- 四變數卡諾圖
- 五變數卡諾圖
- 六變數卡諾圖
- 無關項條件
- 奎因-麥克斯韋方法
- 最小項和最大項
- 規範式和標準式
- 最大項表示
- 使用布林代數化簡
- 組合邏輯電路
- 數字組合電路
- 數字算術電路
- 多路選擇器
- 多路選擇器設計流程
- 多路選擇器通用門
- 使用4:1多路選擇器實現2變數函式
- 使用8:1多路選擇器實現3變數函式
- 多路分配器
- 多路選擇器與多路分配器
- 奇偶校驗位生成器和校驗器
- 比較器
- 編碼器
- 鍵盤編碼器
- 優先編碼器
- 譯碼器
- 算術邏輯單元
- 7段LED顯示器
- 程式碼轉換器
- 程式碼轉換器
- 二進位制轉十進位制轉換器
- 十進位制轉BCD轉換器
- BCD轉十進位制轉換器
- 二進位制轉格雷碼轉換器
- 格雷碼轉二進位制轉換器
- BCD轉餘3碼轉換器
- 餘3碼轉BCD轉換器
- 加法器
- 半加器
- 全加器
- 序列加法器
- 並行加法器
- 使用半加器實現全加器
- 半加器與全加器
- 使用與非門實現全加器
- 使用與非門實現半加器
- 二進位制加法/減法器
- 減法器
- 半減器
- 全減器
- 並行減法器
- 使用兩個半減器實現全減器
- 使用與非門實現半減器
- 時序邏輯電路
- 數字時序電路
- 時鐘訊號和觸發
- 鎖存器
- 移位暫存器
- 移位暫存器應用
- 二進位制暫存器
- 雙向移位暫存器
- 計數器
- 二進位制計數器
- 非二進位制計數器
- 同步計數器設計
- 同步計數器與非同步計數器
- 有限狀態機
- 演算法狀態機
- 觸發器
- 觸發器
- 觸發器轉換
- D觸發器
- JK觸發器
- T觸發器
- SR觸發器
- 帶時鐘SR觸發器
- 無時鐘SR觸發器
- 帶時鐘JK觸發器
- JK到T觸發器
- SR到JK觸發器
- 觸發方法:觸發器
- 邊沿觸發觸發器
- 主從JK觸發器
- 競爭冒險現象
- A/D和D/A轉換器
- 模數轉換器
- 數模轉換器
- DAC和ADC積體電路
- 邏輯閘的實現
- 用與非門實現非門
- 用與非門實現或門
- 用與非門實現與門
- 用與非門實現或非門
- 用與非門實現異或門
- 用與非門實現異或非門
- 用或非門實現非門
- 用或非門實現或門
- 用或非門實現與門
- 用或非門實現與非門
- 用或非門實現異或門
- 用或非門實現異或非門
- 使用CMOS實現NAND/NOR門
- 使用與非門實現全減器
- 使用2:1多路選擇器實現與門
- 使用2:1多路選擇器實現或門
- 使用2:1多路選擇器實現非門
- 儲存器件
- 儲存器件
- RAM和ROM
- 快取記憶體儲存器設計
- 可程式設計邏輯器件
- 可程式設計邏輯器件
- 可程式設計邏輯陣列
- 可程式設計陣列邏輯
- 現場可程式設計門陣列
- 數字電子系列
- 數字電子系列
- CPU架構
- CPU架構
- 數位電子資源
- 數位電子 - 快速指南
- 數位電子 - 資源
- 數位電子 - 討論
使用CMOS實現NAND/NOR門
在數位電子學中,NAND和NOR門是兩種用於對多個輸入變數執行布林運算的通用邏輯閘。這些門根據所施加的輸入組合產生輸出。
NAND和NOR門用作數位電路和系統中的基本構建塊。我們可以使用不同的技術(如DTL、RTL、TTL和CMOS)設計和實現NAND和NOR門。本章重點介紹使用CMOS技術實現NAND和NOR門。
在CMOS(互補金氧半導體)技術中,NAND和NOR邏輯閘是透過將NMOS和PMOS電晶體串聯和並聯連線來設計的。下圖顯示了CMOS技術中一個2輸入邏輯閘的框圖。
在深入研究使用CMOS技術的NAND和NOR門之前。讓我們首先分別研究NAND和NOR門的原理。
NAND門
NAND門是NOT門和AND門的組合,其中一個NOT門連線到AND門的輸出端。因此,它也被稱為取反AND門。
$$\mathrm{AND \: Gate \: + \: NOT \: Gate \: = \: NAND \: Gate}$$
下圖顯示了一個雙輸入NAND門的邏輯電路符號:
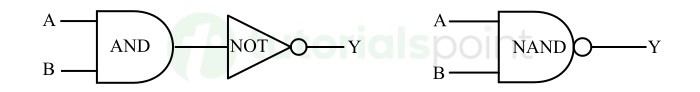
當所有輸入都為高電平或邏輯1時,NAND門產生低電平或邏輯0輸出。對於所有其他輸入組合,它產生高電平或邏輯1輸出。
NAND門的真值表
以下是雙輸入NAND門的真值表:
| 輸入 | 輸出 | |
|---|---|---|
| A | B | Y |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
從這個真值表中,我們可以寫出NAND門的布林表示式,如下所示。
$$\mathrm{Y \: = \: \overline{A\cdot B}}$$
這裡,Y是輸出變數,A和B是輸入變數。
NOR門
NOR門是數位電子學中的一種通用邏輯閘。它是兩個基本邏輯閘的組合,即NOT門和OR門,其中透過將NOT門連線到OR門的輸出端來實現。因此,
$$\mathrm{OR \: Gate \: + \: NOT \: Gate \: = \: NOR \: Gate}$$
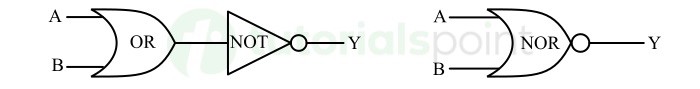
當所有輸入都為低電平或邏輯0時,NOR門的輸出為高電平或邏輯1。對於所有其他輸入組合,NOR門的輸出為低電平或邏輯0。
NOR門的真值表
以下是雙輸入NOR門的真值表,描述了它的操作:
| 輸入 | 輸出 | |
|---|---|---|
| A | B | Y |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
從這個真值表中,我們可以寫出NOR門的布林表示式,如下所示。
$$\mathrm{Y \: = \: \overline{A \: + \: B}}$$
這裡,Y是輸出變數,A和B是輸入變數。
以上是關於NAND和NOR門基本原理的介紹。現在讓我們討論使用CMOS技術實現NAND和NOR門。
使用CMOS技術實現NAND門
可以使用PMOS和NMOS電晶體在CMOS技術中實現NAND門。下圖顯示了CMOS技術中一個雙輸入NAND門的電路圖:
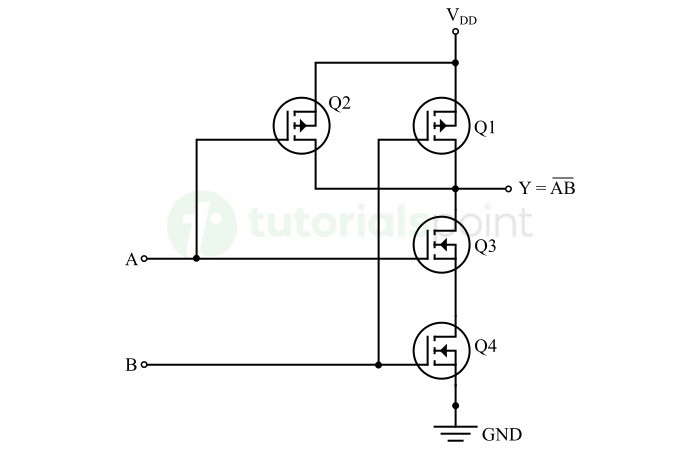
它由兩個PMOS電晶體Q1和Q2以及兩個NMOS電晶體Q3和Q4組成。PMOS電晶體並聯連線在電源VDD和輸出端Y之間。類似地,NMOS電晶體串聯連線在輸出端Y和接地端GND之間。
現在,讓我們瞭解一下這個CMOS NAND門的工作原理。
情況1:當輸入A為低電平且輸入B為低電平時
在這種情況下,當輸入A和B都為低電平時,PMOS電晶體Q1和Q2導通,NMOS電晶體Q3和Q4截止。因此,電源電壓VDD和輸出端Y之間存在一條閉合路徑。
因此,輸出Y將連線到電壓電平VDD。由於兩個NMOS電晶體都截止,因此輸出端和接地端之間沒有路徑。在這種情況下,輸出線將保持VDD的電壓電平,這表示輸出為高電平。
因此,當A = 0且B = 0時,則Y = 1
情況2:當輸入A為低電平且輸入B為高電平時
在這種情況下,PMOS電晶體Q1將導通,而PMOS電晶體Q2將截止。NMOS電晶體Q3將截止,NMOS電晶體Q4將導通。
對於CMOS電晶體的這種切換狀態,電源VDD將透過PMOS電晶體Q1獲得一條通往輸出端的路徑。由於NMOS電晶體Q3和Q4串聯連線,並且NMOS電晶體Q3截止。因此,輸出端和接地端之間沒有路徑。
因此,輸出端Y保持VDD的電壓電平,併產生高電平輸出。
因此,當A = 0且B = 1時,則Y = 1
情況3:當輸入A為高電平且輸入B為低電平時
在這種情況下,PMOS電晶體Q1將截止,PMOS電晶體Q2將導通。NMOS電晶體Q3將導通,NMOS電晶體Q4將截止。
在CMOS電晶體的這種切換狀態下,輸出端將透過PMOS電晶體Q2連線到電源。由於兩個NMOS電晶體串聯連線,並且NMOS電晶體Q4截止。因此,輸出端和接地端之間沒有路徑。
因此,輸出線將保持VDD的電壓電平,併產生高電平輸出。
因此,當A = 1且B = 0時,則Y = 1
情況4:當輸入A為高電平且輸入B為高電平時
在這種情況下,PMOS電晶體Q1和Q2都將截止,並且兩個NMOS電晶體都將導通。在這種情況下,輸出端和電源VDD之間沒有路徑,但輸出端和接地端之間存在一條直通路徑。這導致輸出端出現接地電壓電平,併產生低電平輸出。
因此,當A = 1且B = 1時,則Y = 0
以下真值表顯示了此CMOS NAND門的工作原理:
| 輸入 | 輸出 | |
|---|---|---|
| A | B | Y |
| 低 (0) | 低 (0) | 高 (1) |
| 低 (0) | 高 (1) | 高 (1) |
| 高 (1) | 低 (0) | 高 (1) |
| 高 (1) | 高 (1) | 低 (0) |
以上是關於使用CMOS技術實現NAND門及其在不同輸入組合下的工作原理的介紹。
現在讓我們討論使用CMOS技術實現和操作NOR門。
使用CMOS技術實現NOR門
與CMOS NAND門類似,我們也可以使用PMOS和NMOS電晶體設計NOR門。下圖顯示了使用CMOS技術實現的雙輸入NOR門的電路圖:
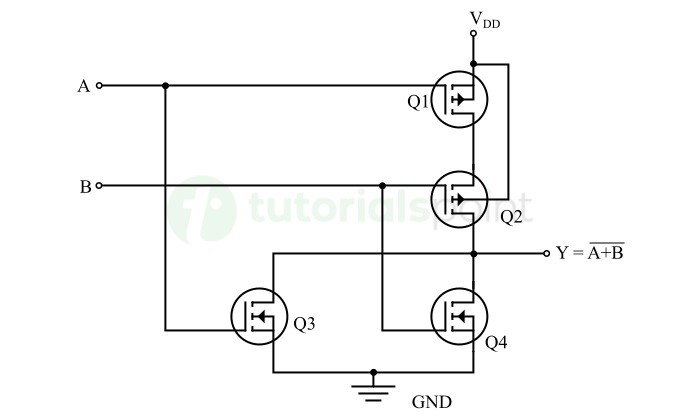
該CMOS NOR門由兩個PMOS電晶體Q1和Q2以及兩個NMOS電晶體Q3和Q4設計而成。其中,PMOS電晶體串聯連線在電源電壓VDD和輸出端Y之間。NMOS電晶體並聯連線在輸出端Y和接地端GND之間。
現在,讓我們瞭解一下這個CMOS電路是如何作為雙輸入NOR門工作的。
情況1:當輸入A為低電平且輸入B為低電平時
在這種情況下,兩個PMOS電晶體Q1和Q2都將導通,而兩個NMOS電晶體Q3和Q4都將截止。
在CMOS電晶體的這種開關狀態下,透過導通的PMOS電晶體,電源電壓VDD和輸出端Y之間存在一條通路。但輸出端Y和接地端GND之間沒有通路。這使得輸出保持在電壓電平VDD,因此輸出將為高電平。
因此,當A = 0且B = 0時,則Y = 1
情況2:當輸入A為低電平且輸入B為高電平時
在這種情況下,PMOS電晶體Q1導通,PMOS電晶體Q2截止,NMOS電晶體Q3截止,NMOS電晶體Q4導通。
由於PMOS電晶體Q1和Q2串聯連線,並且電晶體Q2截止。因此,電源VDD和輸出端Y之間沒有通路。但透過導通的NMOS電晶體Q4,輸出線Y和接地端GND之間存在連線。這將輸出端設定為接地電壓,使輸出為低電平。
因此,當A = 0且B = 1時,則Y = 0
情況3:當輸入A為高電平且輸入B為低電平時
在這種情況下,PMOS電晶體Q1截止,PMOS電晶體Q2導通,NMOS電晶體Q3導通,NMOS電晶體Q4截止。
在這種情況下,由於PMOS電晶體Q1截止,電源VDD和輸出線Y之間沒有閉合通路。但透過導通的NMOS電晶體Q3,輸出線Y和接地端GND之間存在閉合通路。因此,輸出端連線到地電位,使輸出為低電平。
因此,當A = 1且B = 0時,則Y = 0
情況4 – 當輸入A為高電平且輸入B為高電平時
在這種情況下,兩個PMOS電晶體Q1和Q2都截止,兩個NMOS電晶體Q3和Q4都導通。在這種情況下,電源電壓VDD和輸出端Y之間沒有通路。但輸出端Y和接地端GND之間存在閉合通路。這使得輸出線保持在地電壓電平,因此輸出將為低電平。
因此,當A = 1且B = 1時,則Y = 0
CMOS NOR門的完整操作可以總結成真值表的形式,如下所示。
| 輸入 | 輸出 | |
|---|---|---|
| A | B | Y |
| 低 (0) | 低 (0) | 高 (1) |
| 低 (0) | 高 (1) | 低 (0) |
| 高 (1) | 低 (0) | 低 (0) |
| 高 (1) | 高 (1) | 低 (0) |
使用CMOS技術的NAND和NOR門的優點
在CMOS技術中實現的NAND和NOR門比其他技術具有多種優勢。以下是CMOS NAND和NOR門的一些主要優點:
- CMOS NAND和NOR門功耗相對較低。此優點使這些邏輯閘非常適合用於電池供電的裝置。
- 使用CMOS技術設計的NAND和NOR門具有很強的抗噪聲和抗干擾能力。它們可以設計成具有更寬的工作電壓範圍。
- CMOS技術提供了高密度整合,允許在單個晶片上實現大量NAND和NOR門。這些門提供對稱的輸出特性,使它們能夠與不同型別的數位電路無縫整合。
- CMOS技術是一種完善、成熟且經濟高效的半導體制造技術。因此,CMOS NAND和NOR門相對易於製造且成本效益高。
CMOS NAND和NOR門的應用
由於其優勢和多功能性,CMOS NAND和NOR門廣泛應用於以下應用中:
- CMOS NAND和NOR門廣泛用於邏輯電路設計中執行邏輯運算。
- 在數字系統中,CMOS NAND和NOR門用於實現算術電路,如加法器、減法器、乘法器等。
- 它們還用於儲存單元中實現儲存單元結構。
- CMOS NAND和NOR門也用於設計多路複用器和多路分解器。
- CMOS NAND和NOR門的一些其他常見應用包括數字訊號處理、數字定時電路、模數轉換、數字通訊等。
結論
CMOS NAND和NOR門廣泛應用於數位電子領域的各種應用中。這種型別的NAND和NOR門具有多種優點,例如高效率、低功耗、多功能性、低成本、高可靠性等。
在本章中,我們解釋了使用CMOS技術實現NAND和NOR門的方法,以及它們的優點和應用。