
- 數位電子教程
- 數位電子 - 首頁
- 數位電子基礎
- 數字系統的型別
- 訊號的型別
- 邏輯電平和脈衝波形
- 數字系統元件
- 數字邏輯運算
- 數字系統優勢
- 數制
- 數制
- 二進位制數的表示
- 二進位制運算
- 帶符號二進位制運算
- 八進位制運算
- 十六進位制運算
- 補碼運算
- 進位制轉換
- 進位制轉換
- 二進位制到十進位制轉換
- 十進位制到二進位制轉換
- 二進位制到八進位制轉換
- 八進位制到二進位制轉換
- 八進位制到十進位制轉換
- 十進位制到八進位制轉換
- 十六進位制到二進位制轉換
- 二進位制到十六進位制轉換
- 十六進位制到十進位制轉換
- 十進位制到十六進位制轉換
- 八進位制到十六進位制轉換
- 十六進位制到八進位制轉換
- 二進位制編碼
- 二進位制編碼
- 8421 BCD碼
- 餘3碼
- 格雷碼
- ASCII碼
- EBCDIC碼
- 程式碼轉換
- 錯誤檢測與糾錯碼
- 邏輯閘
- 邏輯閘
- 與門
- 或門
- 非門
- 通用門
- 異或門
- 異或非門
- CMOS邏輯閘
- 使用二極體電阻邏輯的或門
- 與門與或門
- 雙電平邏輯實現
- 閾值邏輯
- 布林代數
- 布林代數
- 布林代數定律
- 布林函式
- 德摩根定理
- SOP和POS形式
- POS到標準POS形式
- 最小化技術
- 卡諾圖最小化
- 三變數卡諾圖
- 四變數卡諾圖
- 五變數卡諾圖
- 六變數卡諾圖
- 無關項條件
- 奎因-麥克拉斯基方法
- 最小項和最大項
- 規範式和標準式
- 最大項表示
- 使用布林代數化簡
- 組合邏輯電路
- 數字組合電路
- 數字算術電路
- 多路複用器
- 多路複用器設計流程
- MUX通用門
- 使用4:1MUX的2變數函式
- 使用8:1MUX的3變數函式
- 多路分解器
- MUX與DEMUX
- 奇偶校驗位生成器和校驗器
- 比較器
- 編碼器
- 鍵盤編碼器
- 優先編碼器
- 譯碼器
- 算術邏輯單元
- 7段LED顯示器
- 程式碼轉換器
- 程式碼轉換器
- 二進位制到十進位制轉換器
- 十進位制到BCD轉換器
- BCD到十進位制轉換器
- 二進位制到格雷碼轉換器
- 格雷碼到二進位制轉換器
- BCD到餘3碼轉換器
- 餘3碼到BCD轉換器
- 加法器
- 半加器
- 全加器
- 序列加法器
- 並行加法器
- 使用半加器的全加器
- 半加器與全加器
- 使用與非門的全加器
- 使用與非門的半加器
- 二進位制加法/減法器
- 減法器
- 半減器
- 全減器
- 並行減法器
- 使用2個半減器的全減器
- 使用與非門的半減器
- 時序邏輯電路
- 數字時序電路
- 時鐘訊號和觸發
- 鎖存器
- 移位暫存器
- 移位暫存器應用
- 二進位制暫存器
- 雙向移位暫存器
- 計數器
- 二進位制計數器
- 非二進位制計數器
- 同步計數器設計
- 同步計數器與非同步計數器
- 有限狀態機
- 演算法狀態機
- 觸發器
- 觸發器
- 觸發器轉換
- D觸發器
- JK觸發器
- T觸發器
- SR觸發器
- 帶時鐘的SR觸發器
- 無時鐘的SR觸發器
- 帶時鐘的JK觸發器
- JK到T觸發器
- SR到JK觸發器
- 觸發方法:觸發器
- 邊沿觸發觸發器
- 主從JK觸發器
- 競爭冒險現象
- A/D和D/A轉換器
- 模數轉換器
- 數模轉換器
- DAC和ADC積體電路
- 邏輯閘的實現
- 用與非門實現非門
- 用與非門實現或門
- 用與非門實現與門
- 用與非門實現或非門
- 用與非門實現異或門
- 用與非門實現異或非門
- 用或非門實現非門
- 用或非門實現或門
- 用或非門實現與門
- 用或非門實現與非門
- 用或非門實現異或門
- 用或非門實現異或非門
- 使用CMOS的與非/或非門
- 使用與非門的全減器
- 使用2:1MUX的與門
- 使用2:1MUX的或門
- 使用2:1MUX的非門
- 儲存器件
- 儲存器件
- RAM和ROM
- 快取記憶體儲存器設計
- 可程式設計邏輯器件
- 可程式設計邏輯器件
- 可程式設計邏輯陣列
- 可程式設計陣列邏輯
- 現場可程式設計門陣列
- 數字電子系列
- 數字電子系列
- CPU架構
- CPU架構
- 數位電子資源
- 數位電子 - 快速指南
- 數位電子 - 資源
- 數位電子 - 討論
數位電子中的與門
在數位電子學中,有幾種不同型別的邏輯閘,例如與門、或門、非門等。在本章中,我們將解釋**與門的理論**。
與門是一種基本邏輯閘,用於實現各種複雜的數位電路和系統。與門對施加在其上的輸入執行邏輯乘法,並相應地產生輸出。
什麼是與門?
**與門**是一種用於各種數位電路和系統中的基本邏輯閘型別。僅當所有輸入都為高電平或邏輯1或真時,它才會產生高電平或邏輯1或真的輸出。對於所有其他輸入組合,它都會產生低電平或邏輯0或假的輸出。
兩個和三個輸入與門的邏輯符號如下圖所示。
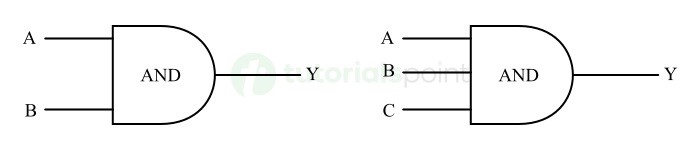
這裡,**A、B**和**C**是輸入變數,**Y**是輸出變數。
在本章中,我們將僅介紹具有三個輸入的與門。但我們可以為任意數量的輸入變數設計與門。
與門的真值表
與門的真值表包含輸入和輸出,並指定它們之間的關係。
雙輸入與門的真值表如下所示:
| 輸入 | 輸出 | |
|---|---|---|
| A | B | Y |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
從雙輸入與門的這個真值表中可以看出,只有當兩個輸入都為邏輯1或高電平時,與門的輸出才為邏輯1或高電平。
下表表示**三輸入與門**的真值表:
| 輸入 | 輸出 | ||
|---|---|---|---|
| A | B | C | Y |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
此真值表顯示,只有當與門的所有三個輸入都為高電平或邏輯1時,輸出才為高電平或邏輯1。對於其餘輸入組合,輸出為低電平或邏輯0。
從這些與門的真值表中,我們可以得出結論:只有當所有輸入都為高電平或邏輯1時,與門才會產生高電平或邏輯1的輸出,否則輸出為低電平或邏輯0。
與門的工作原理
雙輸入與門的工作原理如下所示:
- 如果A = 0且B = 0,則輸出為低電平,即Y = 0。
- 如果A = 0且B = 1,則輸出為低電平,即Y = 0。
- 如果A = 1且B = 0,則輸出為低電平,即Y = 0。
- 如果A = 1且B = 1,則輸出為高電平,即Y = 1。
三輸入與門的工作原理如下所示:
- 如果A = 0,B = 0,C = 0,則輸出為低電平,即Y = 0。
- 如果A = 0,B = 0,C = 1,則輸出為低電平,即Y = 0。
- 如果A = 0,B = 1,C = 0,則輸出為低電平,即Y = 0。
- 如果A = 0,B = 1,C = 1,則輸出為低電平,即Y = 0。
- 如果A = 1,B = 0,C = 0,則輸出為低電平,即Y = 0。
- 如果A = 1,B = 0,C = 1,則輸出為低電平,即Y = 0。
- 如果A = 1,B = 1,C = 0,則輸出為低電平,即Y = 0。
- 如果A = 1,B = 1,C = 1,則輸出為高電平,即Y = 1。
這就是關於雙輸入和三輸入與門工作原理的所有內容。
與門的布林表示式
布林表示式是一個邏輯方程或邏輯函式,它表示與門輸入和輸出之間的數學關係。
雙輸入與門的布林表示式由下式給出:
Y = A · B
其中,**A**和**B**是輸入,**Y**是輸出。此表示式讀作“Y等於A與B”。點 (·) 符號表示與運算。
對於三輸入與門,布林表示式由下式給出:
Y = A · B · C
它讀作“Y等於A與B與C”。
以同樣的方式,我們可以獲得具有任意數量輸入變數的與門的布林表示式。
使用電晶體的與門
雙輸入與門的電晶體電路如下圖所示。
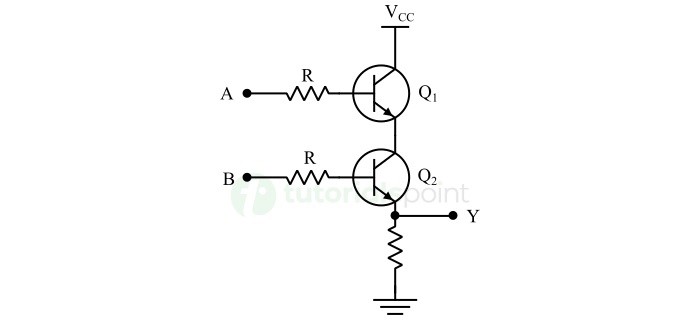
使用電晶體實現與門需要與輸入數量一樣多的電晶體。例如,雙輸入與門需要兩個電晶體。
電晶體與門的工作原理
上面圖中所示的電晶體與門的工作原理如下所述:
**當兩個輸入A和B都為低電平時**,電晶體Q1和Q2保持關閉狀態並充當開路開關。因此,輸出線Y將直接連線到接地電位。因此,輸出為低電平或邏輯0。
**當輸入A為低電平且輸入B為高電平時**,第一個電晶體Q1關閉,第二個電晶體Q2開啟。但電源電壓仍然不會連線到輸出線,輸出線將保持接地電位。因此,輸出為低電平或邏輯0。
**當輸入A為高電平且輸入B為低電平時**,電晶體Q1將導通,電晶體Q2將保持關閉狀態。在這種情況下,輸出線不會接收電源電壓,而是連線到接地電位。因此,對於這種輸入組合,輸出為低電平或邏輯0。
**當兩個輸入A和B都為高電平時**,兩個電晶體Q1和Q2都將開啟並充當閉合開關。在這種情況下,電源電壓直接連線到輸出線。這使得電路的輸出為高電平或邏輯1。
這就是上面電晶體電路如何充當雙輸入與門。我們可以新增更多電晶體來實現高階與門。
使用開關的與門
我們還可以使用電池、開關和燈泡或燈泡來實現與門邏輯。下圖顯示了使用開關的與門。
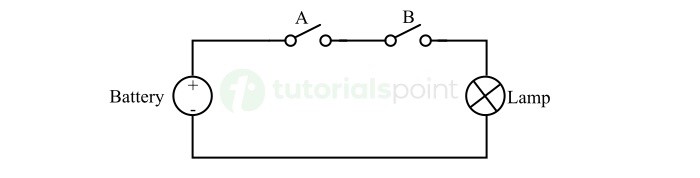
在這個與閘電路中,我們有一個電壓源,兩個開關代表與門的兩個輸入端,一個燈泡代表輸出。
從電路圖可以看出,如果開關A和B都閉合,電流就會有閉合迴路可以流動。因此,燈泡會亮起,表示高電平或邏輯1輸出。
如果兩個開關中的任何一個或兩個都斷開,電流路徑就會斷開,導致燈泡熄滅。這表示與門輸出的低電平或邏輯0狀態。
這樣,上面所示的開關電路就實現了與門運算。透過串聯增加更多開關,我們可以實現更高階的與門。
與門IC
在實際應用中,有一種名為IC 7408的積體電路,它是最常用的與門IC。這種與門IC採用電晶體-電晶體邏輯(TTL)實現。與門IC 7408的框圖如下所示。
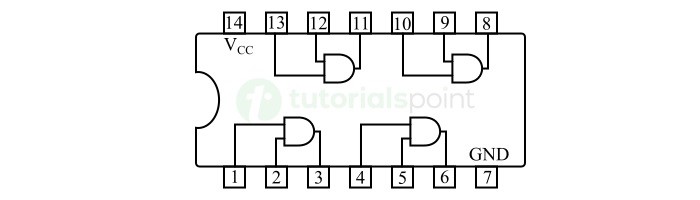
它是一個四2輸入與門IC,在一個晶片上集成了四個雙輸入與門。它有14個引腳。
結論
總之,與門是一種基本的邏輯閘,用於數位電路中實現布林乘法運算。
只有當與門的所有輸入都為高電平或邏輯1時,其輸出才為高電平或邏輯1。否則,它會產生低電平或邏輯0輸出。
與門在各種數位電子應用中發揮著重要作用,例如資料處理、儲存器裝置、算術邏輯單元、控制系統等等。