統計學 - 瑞利分佈

上一頁
下一頁

瑞利分佈是一種連續機率密度函式的分佈。它以英國瑞利勳爵命名。此分佈廣泛用於以下方面：

  • 通訊 - 用於模擬到達接收器的密集散射訊號的多個路徑。

  • 物理科學 - 用於模擬風速、波高、聲音或光輻射。

  • 工程 - 用於根據物體的年齡檢查其壽命。

  • 醫學影像 - 用於模擬磁共振成像中的噪聲方差。

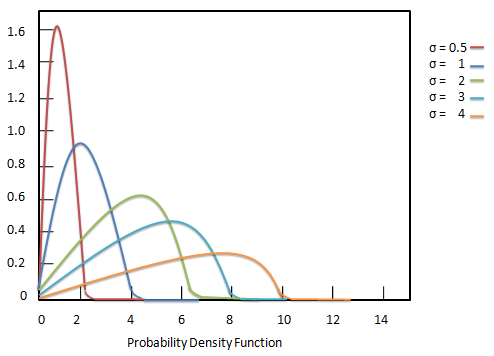
Rayleigh Distribution

瑞利分佈的機率密度函式定義為

公式

${ f(x; \sigma) = \frac{x}{\sigma^2} e^{\frac{-x^2}{2\sigma^2}}, x \ge 0 }$

其中 -

  • ${\sigma}$ = 分佈的尺度引數。

瑞利分佈的累積分佈函式定義為

公式

${ F(x; \sigma) = 1 - e^{\frac{-x^2}{2\sigma^2}}, x \in [0 \infty}$

其中 -

  • ${\sigma}$ = 分佈的尺度引數。

方差和期望值

瑞利分佈的期望值或平均值由下式給出

${ E[x] = \sigma \sqrt{\frac{\pi}{2}} }$

瑞利分佈的方差由下式給出

${ Var[x] = \sigma^2 \frac{4-\pi}{2} }$

列印頁面
上一頁
下一頁
廣告

© . All rights reserved.