
- 統計教程
- 首頁
- 調整 R 方
- 方差分析
- 算術平均數
- 算術中位數
- 算術眾數
- 算術極差
- 條形圖
- 最佳點估計
- β 分佈
- 二項分佈
- 布萊克-斯科爾斯模型
- 箱線圖
- 中心極限定理
- 切比雪夫定理
- 卡方分佈
- 卡方表
- 環狀排列
- 整群抽樣
- 科恩 Kappa 係數
- 組合
- 可重複組合
- 比較圖表
- 連續均勻分佈
- 連續數列算術平均數
- 連續數列算術中位數
- 連續數列算術眾數
- 累積頻率
- 變異係數
- 相關係數
- 累積圖
- 累積泊松分佈
- 資料收集
- 資料收集 - 問卷設計
- 資料收集 - 觀察法
- 資料收集 - 案例研究法
- 資料模式
- 統計分位數
- 離散數列算術平均數
- 離散數列算術中位數
- 離散數列算術眾數
- 點圖
- 指數分佈
- F 分佈
- F 檢驗表
- 階乘
- 頻率分佈
- 伽瑪分佈
- 幾何平均數
- 幾何機率分佈
- 擬合優度
- 總平均數
- Gumbel 分佈
- 調和平均數
- 調和數
- 諧振頻率
- 直方圖
- 超幾何分佈
- 假設檢驗
- 個體數列算術平均數
- 個體數列算術中位數
- 個體數列算術眾數
- 區間估計
- 逆伽瑪分佈
- Kolmogorov-Smirnov 檢驗
- 峰度
- 拉普拉斯分佈
- 線性迴歸
- 對數伽瑪分佈
- 邏輯迴歸
- 麥克尼馬爾檢驗
- 平均差
- 均值差異
- 多項分佈
- 負二項分佈
- 正態分佈
- 奇排列和偶排列
- 單比例 Z 檢驗
- 異常值函式
- 排列
- 可重複排列
- 餅圖
- 泊松分佈
- 合併方差 (r)
- 功效計算器
- 機率
- 機率加法定理
- 機率乘法定理
- 機率貝葉斯定理
- 機率密度函式
- 過程能力 (Cp) 和過程效能 (Pp)
- 過程 sigma
- 二次迴歸方程
- 定性資料與定量資料
- 四分位差
- 經驗法則
- 瑞利分佈
- 迴歸截距置信區間
- 相對標準差
- 信度係數
- 所需樣本量
- 殘差分析
- 殘差平方和
- 均方根
- 樣本計劃
- 抽樣方法
- 散點圖
- 夏農-維納多樣性指數
- 信噪比
- 簡單隨機抽樣
- 偏度
- 標準差
- 標準誤 (SE)
- 標準正態表
- 統計顯著性
- 統計公式
- 統計符號
- 莖葉圖
- 分層抽樣
- 學生 t 檢驗
- 平方和
- t 分佈表
- TI-83 指數迴歸
- 變換
- 截尾均值
- I 型和 II 型錯誤
- 方差
- 維恩圖
- 大數弱定律
- Z 表
- 統計有用資源
- 統計 - 討論
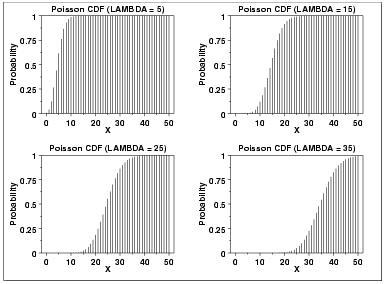
統計 - 累積泊松分佈
λ 是形狀引數,表示給定時間間隔內的平均事件數。以下是四個 λ 值的泊松機率密度函式圖。累積分佈函式。
公式
$${F(x,\lambda) = \sum_{k=0}^x \frac{e^{- \lambda} \lambda ^k}{k!}}$$
其中 −
e = 自然對數的底數,等於 2.71828
k = 事件發生的次數;其機率由該函式給出。
k! = k 的階乘
λ = 正實數,等於給定區間內事件的預期發生次數
示例
問題陳述
一個複雜的軟體系統平均每 5000 行程式碼有 7 個錯誤。在隨機選擇的 5000 行程式碼中,恰好有 2 個錯誤的機率是多少?
解答
在隨機選擇的 5000 行程式碼中,恰好有 2 個錯誤的機率是
${ p(2,7) = \frac{e^{-7} 7^2}{2!} = 0.022}$
廣告