
- Matplotlib 基礎
- Matplotlib - 首頁
- Matplotlib - 簡介
- Matplotlib - 與 Seaborn 的比較
- Matplotlib - 環境設定
- Matplotlib - Anaconda 發行版
- Matplotlib - Jupyter Notebook
- Matplotlib - Pyplot API
- Matplotlib - 簡單繪圖
- Matplotlib - 儲存圖形
- Matplotlib - 標記
- Matplotlib - 圖形
- Matplotlib - 樣式
- Matplotlib - 圖例
- Matplotlib - 顏色
- Matplotlib - 色圖
- Matplotlib - 色圖歸一化
- Matplotlib - 選擇色圖
- Matplotlib - 色標
- Matplotlib - 文字
- Matplotlib - 文字屬性
- Matplotlib - 子圖示題
- Matplotlib - 影像
- Matplotlib - 影像蒙版
- Matplotlib - 註釋
- Matplotlib - 箭頭
- Matplotlib - 字型
- Matplotlib - 什麼是字型?
- 全域性設定字型屬性
- Matplotlib - 字型索引
- Matplotlib - 字型屬性
- Matplotlib - 刻度
- Matplotlib - 線性和對數刻度
- Matplotlib - 對稱對數和 Logit 刻度
- Matplotlib - LaTeX
- Matplotlib - 什麼是 LaTeX?
- Matplotlib - 用於數學表示式的 LaTeX
- Matplotlib - 註釋中的 LaTeX 文字格式
- Matplotlib - PostScript
- 在註釋中啟用 LaTeX 渲染
- Matplotlib - 數學表示式
- Matplotlib - 動畫
- Matplotlib - 圖形物件
- Matplotlib - 使用 Cycler 進行樣式設定
- Matplotlib - 路徑
- Matplotlib - 路徑效果
- Matplotlib - 變換
- Matplotlib - 刻度和刻度標籤
- Matplotlib - 弧度刻度
- Matplotlib - 日期刻度
- Matplotlib - 刻度格式化器
- Matplotlib - 刻度定位器
- Matplotlib - 基本單位
- Matplotlib - 自動縮放
- Matplotlib - 反轉軸
- Matplotlib - 對數軸
- Matplotlib - Symlog
- Matplotlib - 單位處理
- Matplotlib - 帶單位的橢圓
- Matplotlib - 脊柱
- Matplotlib - 軸範圍
- Matplotlib - 軸刻度
- Matplotlib - 軸刻度
- Matplotlib - 格式化軸
- Matplotlib - Axes 類
- Matplotlib - 雙軸
- Matplotlib - Figure 類
- Matplotlib - 多圖
- Matplotlib - 網格
- Matplotlib - 面向物件介面
- Matplotlib - PyLab 模組
- Matplotlib - Subplots() 函式
- Matplotlib - Subplot2grid() 函式
- Matplotlib - 固定圖形物件
- Matplotlib - 手動等值線
- Matplotlib - 座標報告
- Matplotlib - AGG 過濾器
- Matplotlib - 帶狀框
- Matplotlib - 填充螺旋線
- Matplotlib - Findobj 演示
- Matplotlib - 超連結
- Matplotlib - 影像縮圖
- Matplotlib - 使用關鍵字繪圖
- Matplotlib - 建立 Logo
- Matplotlib - 多頁 PDF
- Matplotlib - 多程序
- Matplotlib - 列印標準輸出
- Matplotlib - 複合路徑
- Matplotlib - Sankey 類
- Matplotlib - MRI 與 EEG
- Matplotlib - 樣式表
- Matplotlib - 背景顏色
- Matplotlib - Basemap
- Matplotlib 事件處理
- Matplotlib - 事件處理
- Matplotlib - 關閉事件
- Matplotlib - 滑鼠移動
- Matplotlib - 點選事件
- Matplotlib - 滾動事件
- Matplotlib - 按鍵事件
- Matplotlib - 選擇事件
- Matplotlib - 放大鏡
- Matplotlib - 路徑編輯器
- Matplotlib - 多邊形編輯器
- Matplotlib - 定時器
- Matplotlib - Viewlims
- Matplotlib - 縮放視窗
- Matplotlib 小部件
- Matplotlib - 游標小部件
- Matplotlib - 帶註釋的游標
- Matplotlib - 按鈕小部件
- Matplotlib - 複選框
- Matplotlib - 套索選擇器
- Matplotlib - 選單小部件
- Matplotlib - 滑鼠游標
- Matplotlib - 多游標
- Matplotlib - 多邊形選擇器
- Matplotlib - 單選按鈕
- Matplotlib - RangeSlider
- Matplotlib - 矩形選擇器
- Matplotlib - 橢圓選擇器
- Matplotlib - 滑塊小部件
- Matplotlib - 跨度選擇器
- Matplotlib - 文字框
- Matplotlib 繪圖
- Matplotlib - 條形圖
- Matplotlib - 直方圖
- Matplotlib - 餅圖
- Matplotlib - 散點圖
- Matplotlib - 箱線圖
- Matplotlib - 小提琴圖
- Matplotlib - 等值線圖
- Matplotlib - 3D 繪圖
- Matplotlib - 3D 等值線
- Matplotlib - 3D 線框圖
- Matplotlib - 3D 曲面圖
- Matplotlib - Quiver 圖
- Matplotlib 有用資源
- Matplotlib - 快速指南
- Matplotlib - 有用資源
- Matplotlib - 討論
Matplotlib - 色圖歸一化
術語歸一化指的是將實數值重新縮放到一個共同的範圍,例如 0 到 1 之間。它通常用作資料處理和分析中的預處理技術。
Matplotlib 中的色圖歸一化
在這種情況下,歸一化是將資料值對映到顏色的過程。Matplotlib 庫提供了各種歸一化技術,包括:
對數
居中
對稱對數
冪律
離散邊界
雙斜率
自定義歸一化
線性歸一化
Matplotlib 中的預設行為是根據指定範圍內的數值線性對映顏色。此範圍通常由matplotlib.colors.Normalize()例項引數的最小值 (vmin) 和最大值 (vmax) 定義。
此對映分兩個步驟進行,首先將輸入資料歸一化到 [0, 1] 範圍,然後對映到色圖中的索引。
示例
此示例使用 matplotlib.colors 模組中的Normalize()類演示了 Matplotlib 的線性歸一化過程。
import matplotlib as mpl
from matplotlib.colors import Normalize
# Creates a Normalize object with a specified range
norm = Normalize(vmin=-1, vmax=1)
# Normalizing a value
normalized_value = norm(0)
# Display the normalized value
print('Normalized Value', normalized_value)
輸出
執行上述程式碼後,我們將獲得以下輸出:
Normalized Value: 0.5
雖然線性歸一化是預設的,並且通常適用,但在某些情況下,非線性對映可能更具資訊量或視覺吸引力。
對數歸一化
這是一種常見的變換,它採用資料的對數(以 10 為底)。當顯示跨不同尺度的變化時,這很有用。colors.LogNorm() 類用於此歸一化。
示例
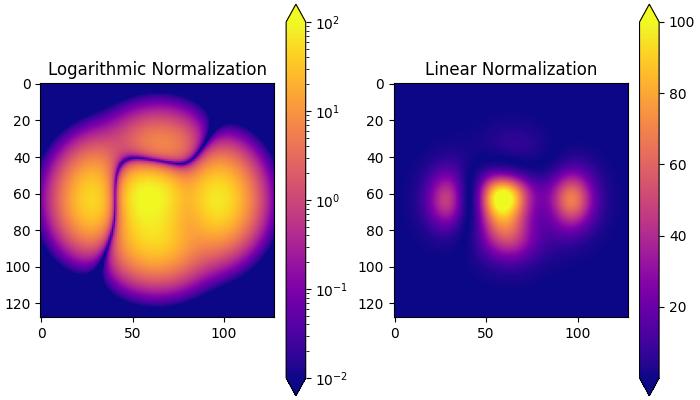
在此示例中,建立了兩個子圖以演示對數歸一化和線性歸一化變換之間的差異。
import matplotlib.pyplot as plt
import numpy as np
from matplotlib import colors
# Sample Data
X, Y = np.meshgrid(np.linspace(-3, 3, 128), np.linspace(-3, 3, 128))
Z = (1 - X/2 + X**5 + Y**3) * np.exp(-X**2 - Y**2)
# Create subplots
fig, ax = plt.subplots(1, 2, figsize=(7,4), layout='constrained')
# Logarithmic Normalization
pc = ax[0].imshow(Z**2 * 100, cmap='plasma',
norm=colors.LogNorm(vmin=0.01, vmax=100))
fig.colorbar(pc, ax=ax[0], extend='both')
ax[0].set_title('Logarithmic Normalization')
# Linear Normalization
pc = ax[1].imshow(Z**2 * 100, cmap='plasma',
norm=colors.Normalize(vmin=0.01, vmax=100))
fig.colorbar(pc, ax=ax[1], extend='both')
ax[1].set_title('Linear Normalization')
plt.show()
輸出
執行上述程式碼後,我們將獲得以下輸出:
居中歸一化
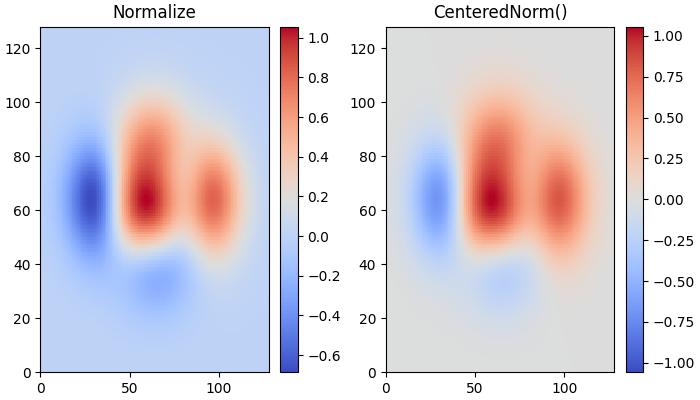
當資料圍繞中心對稱(例如,圍繞 0 的正異常和負異常)時,可以使用colors.CenteredNorm()類。它會自動將中心對映到 0.5,並將與中心偏差最大的點對映到 1.0 或 0.0,具體取決於其值。
示例
此示例比較了預設線性歸一化和居中歸一化 (CenteredNorm()) 對資料集的影響,使用 coolwarm 色圖。
import matplotlib.pyplot as plt
import numpy as np
from matplotlib import colors, cm
X, Y = np.meshgrid(np.linspace(-3, 3, 128), np.linspace(-3, 3, 128))
Z = (1 - X/2 + X**5 + Y**3) * np.exp(-X**2 - Y**2)
# select a divergent colormap
cmap = cm.coolwarm
# Create subplots
fig, ax = plt.subplots(1, 2, figsize=(7,4), layout='constrained')
# Default Linear Normalization
pc = ax[0].pcolormesh(Z, cmap=cmap)
fig.colorbar(pc, ax=ax[0])
ax[0].set_title('Normalize')
# Centered Normalization
pc = ax[1].pcolormesh(Z, norm=colors.CenteredNorm(), cmap=cmap)
fig.colorbar(pc, ax=ax[1])
ax[1].set_title('CenteredNorm()')
plt.show()
輸出
執行上述程式碼後,我們將獲得以下輸出:
對稱對數歸一化
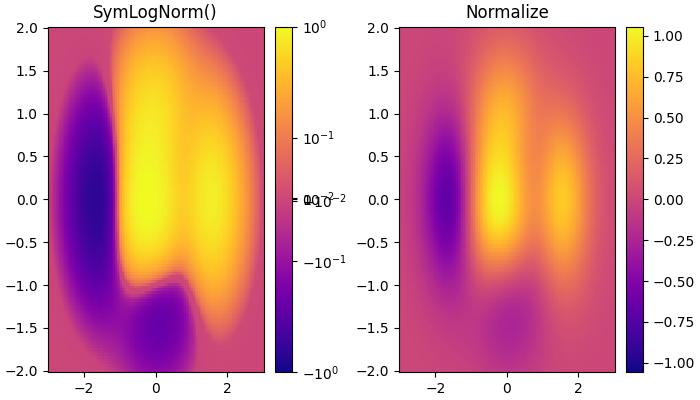
如果資料可能包含正值和負值,並且希望對兩者都進行對數縮放。Matplotlib 中的colors.SymLogNorm()類專為這種情況而設計。此歸一化將負數對數對映到較小的值,並將正數對映到較大的值。
示例
這是一個使用colors.SymLogNorm()類轉換資料的示例。
import matplotlib.pyplot as plt
import numpy as np
from matplotlib import colors, cm
X, Y = np.mgrid[-3:3:complex(0, 128), -2:2:complex(0, 128)]
Z = (1 - X/2 + X**5 + Y**3) * np.exp(-X**2 - Y**2)
# Create subplots
fig, ax = plt.subplots(1, 2, figsize=(7, 4), layout='constrained')
# Symmetric Logarithmic Normalization
pcm = ax[0].pcolormesh(X, Y, Z,
norm=colors.SymLogNorm(linthresh=0.03, linscale=0.03,vmin=-1.0, vmax=1.0, base=10),
cmap='plasma', shading='auto')
fig.colorbar(pcm, ax=ax[0])
ax[0].set_title('SymLogNorm()')
# Default Linear Normalization
pcm = ax[1].pcolormesh(X, Y, Z, cmap='plasma', vmin=-np.max(Z), shading='auto')
fig.colorbar(pcm, ax=ax[1])
ax[1].set_title('Normalize')
plt.show()
輸出
執行上述程式碼後,我們將獲得以下輸出:
冪律歸一化
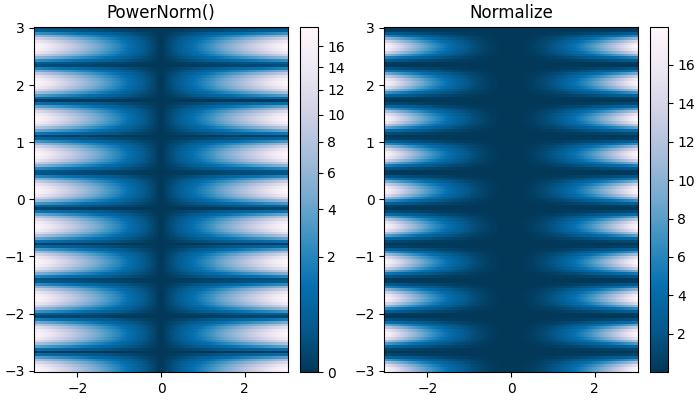
此歸一化可用於使用colors.PowerNorm()類將顏色重新對映到冪律關係。
示例
這是一個比較冪律 (colors.PowerNorm()) 和線性歸一化的示例。
import matplotlib.pyplot as plt
import numpy as np
from matplotlib import colors, cm
X, Y = np.meshgrid(np.linspace(-3, 3, 128), np.linspace(-3, 3, 128))
Z = (1 + np.sin(Y * 10.)) * X**2
# Create subplots
fig, ax = plt.subplots(1, 2, figsize=(7, 4), layout='constrained')
# Power-law Normalization
pcm = ax[0].pcolormesh(X, Y, Z, norm=colors.PowerNorm(gamma=0.5),
cmap='PuBu_r', shading='auto')
fig.colorbar(pcm, ax=ax[0])
ax[0].set_title('PowerNorm()')
# Default Linear Normalization
pcm = ax[1].pcolormesh(X, Y, Z, cmap='PuBu_r', shading='auto')
fig.colorbar(pcm, ax=ax[1])
ax[1].set_title('Normalize')
plt.show()
輸出
執行上述程式碼後,我們將獲得以下輸出:
離散邊界歸一化
Matplotlib 提供的另一種歸一化是colors.BoundaryNorm。當需要在指定邊界之間對映資料並使用線性分佈的顏色時,這特別有用。
示例
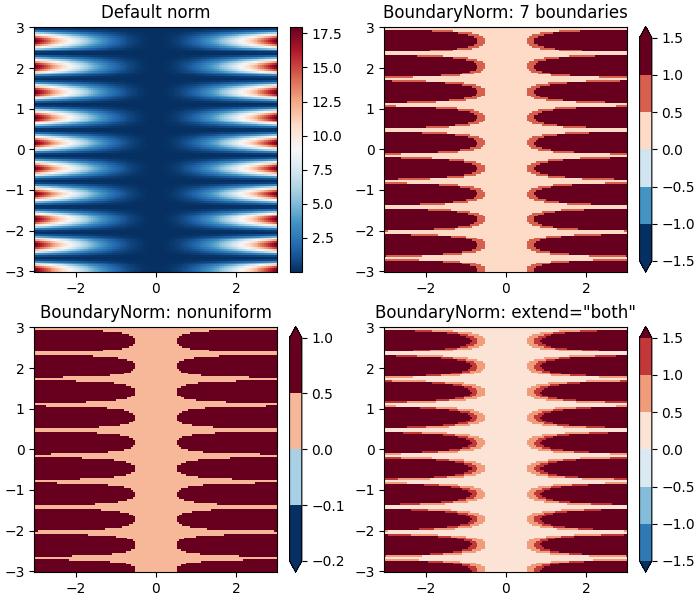
此示例演示了使用BoundaryNorm()類進行離散邊界歸一化的用法,以便在顯示 colormesh 圖時建立不同的視覺效果。
import matplotlib.pyplot as plt
import numpy as np
import matplotlib.colors as colors
X, Y = np.meshgrid(np.linspace(-3, 3, 128), np.linspace(-3, 3, 128))
Z = (1 + np.sin(Y * 10.)) * X**2
fig, ax = plt.subplots(2, 2, figsize=(7, 6), layout='constrained')
ax = ax.flatten()
# Default norm:
pcm = ax[0].pcolormesh(X, Y, Z, cmap='RdBu_r')
fig.colorbar(pcm, ax=ax[0], orientation='vertical')
ax[0].set_title('Default norm')
# Even bounds give a contour-like effect:
bounds = np.linspace(-1.5, 1.5, 7)
norm = colors.BoundaryNorm(boundaries=bounds, ncolors=256)
pcm = ax[1].pcolormesh(X, Y, Z, norm=norm, cmap='RdBu_r')
fig.colorbar(pcm, ax=ax[1], extend='both', orientation='vertical')
ax[1].set_title('BoundaryNorm: 7 boundaries')
# Bounds may be unevenly spaced:
bounds = np.array([-0.2, -0.1, 0, 0.5, 1])
norm = colors.BoundaryNorm(boundaries=bounds, ncolors=256)
pcm = ax[2].pcolormesh(X, Y, Z, norm=norm, cmap='RdBu_r')
fig.colorbar(pcm, ax=ax[2], extend='both', orientation='vertical')
ax[2].set_title('BoundaryNorm: nonuniform')
# With out-of-bounds colors:
bounds = np.linspace(-1.5, 1.5, 7)
norm = colors.BoundaryNorm(boundaries=bounds, ncolors=256, extend='both')
pcm = ax[3].pcolormesh(X, Y, Z, norm=norm, cmap='RdBu_r')
# The colorbar inherits the "extend" argument from BoundaryNorm.
fig.colorbar(pcm, ax=ax[3], orientation='vertical')
ax[3].set_title('BoundaryNorm: extend="both"')
plt.show()
輸出
執行上述程式碼後,我們將獲得以下輸出:
TwoSlopeNorm歸一化用於在概念中心點兩側使用不同的色圖,它通常用於諸如地形圖之類的場景,其中陸地和海洋具有不同的海拔和深度範圍。
當內建規範不足時,FuncNorm允許使用任意函式進行自定義歸一化。
此外,Matplotlib 支援建立自定義歸一化,例如MidpointNormalize,這對於在專業視覺化中定義對映很有用。
這些工具提供了靈活性,可以將顏色表示適應不同的資料和視覺化需求。