能力傾向 - 高度與距離線上測驗

以下測驗提供與高度與距離相關的多項選擇題 (MCQ)。您需要閱讀所有給出的答案，然後點選正確的答案。如果您不確定答案，可以使用顯示答案按鈕檢視答案。您可以使用下一題按鈕檢視測驗中的新一組問題。

問題 1 - 一個站在垂直觀測塔頂端的人觀察到一輛以勻速行駛的汽車正朝塔駛來。如果俯角從 45° 變為 60° 需要 10 分鐘，那麼汽車在此之後多久到達觀測塔？

答案：B

解釋

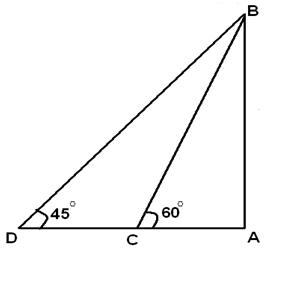
Height & Distance Solution 3

Let AB be the tower and C and D be the two positions of the car.
Then,from figure
AB/AC=tan 60 =√3 => AB=√3AC
AB/AD=tan 45=1 => AB=AD
AB=AC+CD
CD=AB-AC=√3AC - AC=AC (√3-1)
CD = AC (√3-1) =>10 min
 AC=> ?
AC/(AC(√3-1)) x 10=?=10/(√3-1)=13.66=13 min 20 sec(approx)

問題 2 - 當太陽高度角從 45° 變為 60° 時，一座塔的影子長度減少了 45 米。這座塔的高度是多少？

答案：A

解釋

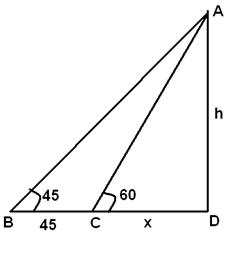
Height & Distance Solution 6

Let AD be the tower, BD be the initial shadow and CD be the final shadow.
Given that BC = 45 m,  ABD = 45°,  ACD = 60°,
Let CD = x, AD = h
From the right   CDA, tan60=h/x
From the right   BDA, tan45=(45+x)/h=>h=45+x
=>h=45+h/√3
=>h(1-1/√3)=45
=>h=45/(1-1/√3)=(45√3)/(√3-1)

問題 3 - 一棵直立的樹因雷雨而折斷。斷裂的部分彎曲，使得樹尖觸地，形成一個仰角 45°。樹尖到樹根的距離是 20 米。那麼這棵樹的高度是多少？

答案：A

解釋

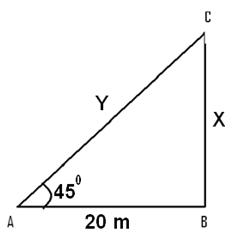
Height & Distance Solution 9

Let the total length of the tree be X+Y meters
From the figure tan 45=X/20 =>X=20
cos 45 = 20/Y =>Y=20/cos 45 =20√2
X+Y=20+20radic;2=20+2x10x1.414 =48.28 meters

問題 4 - 一根 10 米高的旗杆立在一座 50 米高的建築物上。一個觀察者在 60 米的高度上，觀察旗杆和建築物頂端所成的角相等。觀察者到旗杆頂端的距離是多少？

答案：C

解釋

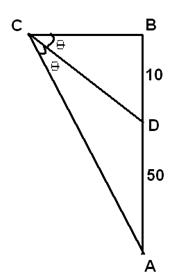
Height & Distance Solution 10

From the figure
tanθ=10/CB
tan(2θ)=60/CB=(2tan(θ))/(1-tan(θ)²)
=>60/CB=(2tan(θ))/(1-tan(θ)²)=(2(10/CB))/(1-(10/CB)²)
=>3/1=1/(1-(10/CB)²)
=>3x(1-(10/CB)sup>2)=1
3CB²-300=CB²
2CB²=300=>CB=√150=5√6

問題 5 - 考慮一個高 6 米的垂直豎井，其影子長 2√3 米，求太陽的仰角？

答案：A

解釋

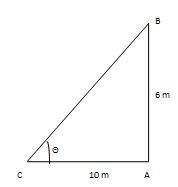
Height & Distance Solution 13

Let AB be the building and AC be its shadow. Then, AB= 6m and AC= 2√3m.
Let ∠ACB= θ Then tan θ = AB/AC= 6/2√3m
 =√3= >θ =60°
Point of rise of the sun is 60°

問題 6 - 從距離塔底 50 米處測得塔頂的仰角為 30°。塔的高度是多少？

答案：B

解釋

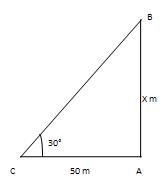
Height & Distance Solution 16

Let AB be the tower and AC be the even line such that AC=50 m and ∠ACB=30°.
AB/AC=tan 30°=1/√3
=>x/50 = 1/√3
> x=50*1/√3m= 50/√3m.
∴ Height of the tower=50/√3m.

問題 7 - 從一個高 90 米的懸崖頂端，觀察到一座塔的頂部和底部的俯角分別為 30° 和 60°。這座塔的高度是多少？

答案：C

解釋

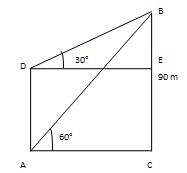
Height & Distance Solution 21

Let AB be the precipice and CD be the tower. Draw DE || CA.
Then, ∠BDE=30°, ∠BCA=60°and AB= 90m.
From right △CAB, we have
CA/AB=cost60°=1/√3 => CA/90=1/√3
=>CA=(90*1/√3* √3/√3)
=30 √3m.
∴ DE =CE=30/√3m.
From right ?DEB, we have
BE/DE= tan30°=1/√3 => BE/30 √3=1 √3
=>BE= (30 √3*1 √3) =30m.
∴ CD=AE= (AB-BE) = (90-30) m=60m.
Hence, the tower's stature is 60m.

問題 8 - 在水平地面上，有一座豎直的塔，塔頂有一根旗杆。在距離塔 9 米處，觀察到旗杆頂端和底部的仰角分別為 60° 和 30°。旗杆的高度是多少？

答案：A

解釋

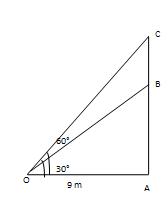
Height & Distance Solution 25

Let AB be the tower and BC be the flag pole and let O be the point of observation.
Then, A=9m, ∠AOB=30°and ∠AOC=60°
AB/OA=tan30°=1 ∠ =>AB/9=1∠
=>AB=(9*1/ √3* √3/√3)= 3 √3m.
AC/AO=tan60°=√3 =>AC/9= √3 =>AC= 9√3m.
∴BC= (AC-AB) = (9 √3-3 √3) m=6 √3m.
∴ Height of the flagpole is 6 √m.

aptitude_height_distance.htm

列印頁面