能力傾向 - 解析幾何

---

---

平面上的點的位置

在座標幾何中，點放置在“座標平面”上，如下所示。它有兩個刻度 - 一個橫跨平面稱為“x 軸”，另一個與之成直角稱為 y 軸。（這些可以被認為類似於上面段落中的列和行。）軸線交叉的點稱為原點，x 和 y 都為零。

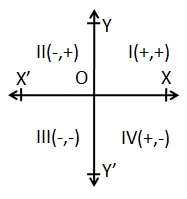
在 x 軸上，右邊的值為正，左邊的值為負。在 y 軸上，原點上方的值為正，原點下方的值為負。平面上的點的位置由兩個數字給出；第一個表示它在 x 軸上的位置，第二個表示它在 y 軸上的位置。它們一起定義了平面上唯一的單一位置。因此，在上圖中，點 A 的 x 值為 20，y 值為 15。這些是點 A 的座標，有時稱為其“直角座標”。

請注意，順序很重要；x 座標始終是這對中的第一個。

兩點之間的距離

如果 A(x₁,y₁) 和 B (x₂,y₂) 是兩點，則

AB =√(x2-x1)2 + (y2-y1)2

點到原點的距離

點 A(x, y) 到原點 O(0, 0) 的距離由下式給出

OA =√(x2+y2)

三角形的面積

如果 A(x₁,y₁)、B(x₂,y₂) 和 C= (X₃, Y₃) 是 ∆ABC 的三個頂點，則其面積由下式給出

∆ = 1/2 {x1(y2- Y3)+ x2(Y3- Y1) +X3(y1-y2)}

三點共線的條件

三點 A(x₁,y₁)、B(x₂,y₂) 和 C= (X₃, Y₃) 共線當且僅當 ar(√ABC)= 0。

∴ A、B、C 共線 ⇒ x₁(y₂- Y₃)+ x₂(Y₃- Y₁) +X₃(y₁-y₂) = 0

點分割線段

如果點 p(x,y) 以 m:n 的比例分割 A(x₁,y₁) 和 B(x₂,y₂) 的連線，則

X= (mx2+nx1)/m+n and Y =(my2+ny1)/m+n

如果 A(x₁,y₁) 和 B(x₂,y₂) 是線段 AB 的端點，則 AB 中點的座標為

[(x1 + x2)/ 2 , (y1 + y2)/ 2]

三角形的重心

三角形所有中線的交點稱為其重心。如果 A(x₁,y₁)、B(x₂,y₂) 和 C= (X₃, Y₃) 是 ABC 的頂點，則其重心的座標為 { (1/3 (x₁+x₂+x₃),1/3 (y₁+y₂+Y₃)}

各種型別的四邊形

四邊形是

• 如果其對邊相等且對角線相等，則為矩形。

• 如果其對邊相等且對角線不相等，則為平行四邊形但不是矩形。

• 如果所有邊都相等且對角線相等，則為正方形。

• 如果所有邊都相等且對角線不相等，則為菱形但不是正方形。

直線的方程

• x 軸的方程為 y =0。

• y 軸的方程為 x = 0。

• 與 y 軸平行且與之相距 a 的直線的方程為 x= a。

• 與 x 軸平行且與之相距 b 的直線的方程為 y= b。

• 經過點 A(x₁,y₁) 和 B(x₂,y₂) 的直線的方程為 y-y₁/ x-x₁ = y₂-y₁/x₂-x₁。此直線的斜率為 y₂-y₁/x₂-x₁。

• 直線在斜截式中的方程為 Y= mx+ c，其中 m 是其斜率。

解題示例

解題示例