推理 - 符號序列
骰子是一個小立方體,可以在骰子的六個面上畫上許多點、字母、數字或圖形。在候選人選拔過程中,經常會問到骰子問題。可以透過摺疊一塊預先確定形狀的紙片(如圖所示,包含六個正方形)來製作骰子的六個面。
讓我們來看這樣一張紙 ,它可以按以下方式摺疊成一個立方體。
,它可以按以下方式摺疊成一個立方體。

骰子的各個面在圖中已描述。

在競爭性考試中,會要求考生解答各種基於影像形式的骰子不同部分的題目,例如尋找相對面、底面等。題目也可能基於一個展開的圖形,這個圖形可以摺疊成一個立方體/骰子。
為了找到相對面,考生可能會得到骰子的各種影像,這些影像顯示了骰子的兩個、三個或四個位置。考生必須比較骰子六個面上給出的各種圖形、數字或字母來得到答案。
在解答骰子問題之前,考生應該能夠熟練地分析圖形並確定圖形、字母或數字在骰子六個面上的精確位置。骰子的兩個面之間主要存在兩種關係:它們彼此相對(如正面和背面)或彼此相鄰。下面的例子可以清楚地解釋這個問題。
假設在骰子的六個面上寫有從1到6的數字。
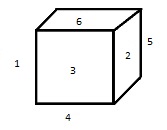
在圖中,相對面是1-2、3-5和4-6,而1、2、4和6與3和5相鄰。需要注意的是,相對面總是與同一組面相鄰,例如圖中所示的3和5。
題目主要用來尋找相對面,這可以透過將與所提問的字母、圖形或數字相鄰的字母、圖形或數字進行等同來解決。等同後剩下的字母、圖形或數字就是相對面。也可以透過根據題目圖形繪製骰子的展開圖來解答題目,這在各種情況中都有所討論。
情況一
給出骰子的兩個位置
示例
給出了一個骰子的兩個位置,其面從1到6編號。
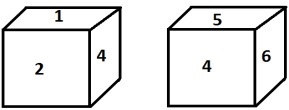
哪個數字與3相對?
選項 −
A - 4
B - 5
C - 6
D - 2
答案 − 選項A
解釋 − 在給定的圖形中,4是骰子兩個位置的共同面,由此可以看出,4的相鄰面是1、2、5和6。因此,在將4的相鄰面等同後剩下3,所以3一定在4的相對面,反之亦然。
情況二
給出骰子的三個視角。
在這種情況下,題目可能會要求找出相對面,或者給定的題目圖形中,骰子的某個視角會缺少某個字元,考生必須根據給定的題目圖形比較各種字母、圖形或數字,以找出答案的字母、圖形或數字。
示例一
圖中給出了骰子的三個位置。

哪個數字與6相對?
選項 −
A - 1
B - 3
C - 4
D - 2
答案 − 選項D
解釋 − 從圖(i)和(ii)可以看出,1、3、4和5與2相鄰,因此只有6與2相對,反之亦然。也可以透過根據題目圖形繪製骰子的展開圖來解答,如下所示:

題目也可能會要求找出缺失的字母、圖形或數字。讓我們在下面的例子中看看這一點。
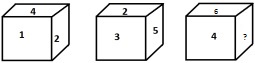
哪個數字將替換問號?
選項 −
A - 3
B - 4
C - 5
D - 6
答案 − 選項D
解釋 − 從展開圖可以看出,1、4、3和5與2相鄰,表明6在其相對面。骰子的展開圖可以繪製如下。
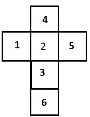
情況三
在一些考試中,考生可能會得到骰子的四個位置,可能會提出與給定圖形相關的各種問題,例如:
題目圖形中給出的骰子任何位置的底面或背面。
根據題目圖形選擇某些陳述正確或不正確。
找出相對面的對。
例如,考慮以下骰子的位置

1 - 圖(iii)的底面上是什麼字母?
選項 −
A - A
B - B
C - C
D - D
答案 − 選項B
解釋 − 我們可以從圖(i)和(ii)繪製展開圖,A、C和D與B相鄰;從圖(i)、(ii)和(iii)可以看出,A、B、C和F與D相鄰,因此

2 - 哪個陳述是正確的?
選項 −
A - A和C是相對面
B - 圖(iii)的背面是D
C - 兩者都正確
D - 都不對
答案 − 選項C
解釋 − 從展開圖可以看出,選項(c)是答案。

情況四
有時可能會給出骰子的展開圖,考生必須根據圖形回答各種問題,這些問題可能是從給出的備選答案中選擇相似的骰子,或者也可能要求找出相對面。這類問題可以透過繪製骰子的摺疊圖來解答,這裡用例子來解釋,讓我們來看一下骰子的以下展開圖。

哪個骰子與題目圖形相似?

答案 − 選項D
解釋 − 從題目圖形可以繪製出骰子的摺疊圖,表明選項(d)與題目圖形相似。

