推理 - 邏輯推演
邏輯推演是一個重要的章節,因為各種競爭性考試中都包含了許多來自該章節的簡單且得分高的題目。在本節中,我們將討論兩種解決此類問題的方法:
- 三段論方法
- 韋恩圖方法
基礎
如果有兩個陳述,那麼三段論將是解決問題的最佳方法,但如果陳述的數量超過兩個,則使用韋恩圖方法。有時,陳述和結論源於普遍接受的事實,但它們也可能是不合邏輯的。例如:
a) 一些椅子是門。
b) 所有男人都是女人
c) 沒有牛奶是白色的
得出結論需要抽象思維。需要理解句子的邏輯含義,然後根據邏輯含義回答結論。每個陳述都需要被認為是真實的,然後我們必須驗證結論是否在邏輯上遵循陳述。
限定詞
這些是一些用來描述一樣東西與另一樣東西有多相似或不同的基本詞彙。一些限定詞的例子包括“所有”、“一些”、“一些不”等。
韋恩圖概念
另一方面,韋恩圖是一種方法,我們可以用幾何圖形的形式表示句子或陳述。所有給定的陳述都繪製在可能的韋恩圖中。然後用這些圖驗證所有結論。任何滿足所有韋恩圖的結論都將被視為有效結論。
| 陳述 | 對應的韋恩圖 |
|---|---|
| 所有 A 都是 B | 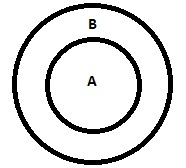 |
| 一些 A 是 B(或)一些 A 不是 B | 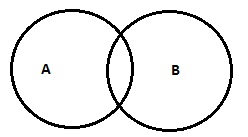 |
| 沒有 A 是 B | 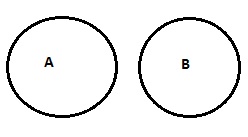 |
讓我們舉一個簡單的例子來更好地理解它。
示例 - 1
陳述 -
所有工程師都是傻瓜。所有傻瓜都是醫生。所有醫生都是窮人。
結論 -
I. 一些窮人是傻瓜。
II. 一些窮人是工程師。
選項 -
A - 只有 I 有效
B - 只有 II 有效
C - 兩個陳述都有效
D - 兩個陳述均無效
答案 - 選項 C
解釋 -
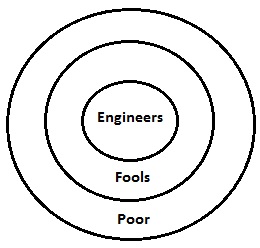
給定陳述的韋恩圖如上所示。它以圖解的方式將所有陳述集中在一個地方。現在,如果我們逐一討論結論,一切都會變得清晰。
這裡傻瓜是窮人的子集。因此,很明顯一些窮人將是傻瓜。因此,結論 I 有效。同樣,結論 II 有效,因為工程師也是窮人的子集。因此,兩個陳述都有效。
示例 - 2
陳述 -
一些鍵盤是滑鼠。一些滑鼠是收音機。
結論 -
I. 一些鍵盤是收音機。
II. 一些收音機是鍵盤
III. 所有收音機都是滑鼠。
IV. 所有滑鼠都是鍵盤。
選項 -
A - 只有結論 I 有效
B - 只有結論 II 有效
C - I 或 II 有效
D - 沒有結論有效
E - I 和 II 均有效
答案 - 選項 D
解釋 - 由於兩個陳述都是特定的,因此沒有明確的結論有效。
示例 - 3
陳述 -
所有學生都是清醒的。所有學生都是淘氣的。
結論 -
I. 所有淘氣的要麼是清醒的,要麼反之亦然。
II. 一些清醒的人是淘氣的。
III. 通常淘氣的人是清醒的。
IV. 犯罪和內疚是相伴而生的。
選項 -
A - 只有結論 I 有效
B - 只有結論 II 有效
C - I 或 II 有效
D - I 或 II 均無效
E - I 和 II 均有效
答案 - 選項 B
解釋 - 由於中間項“學生”在陳述中被分配了兩次,因此結論不能太寬泛。因此,有效的是“一些清醒的人是淘氣的”。因此,II 成立。
