推理 - 三段論
希臘人給出的三段論的含義是演繹。這是一種邏輯論證。
一些重要術語的定義
下面給出一些術語,這些術語在解決三段論問題中起著重要作用。
命題 - 命題是一個陳述句。命題由三部分組成:a) 主語,b) 謂語,c) 主語和謂語之間的關係。下面給出一些命題。
- 所有海岸都是海灘。
- 沒有學生是誠實的。
- 有些檔案是秘密的。
主語和謂語 - 主語是被敘述的物件。另一方面,謂語是與主語相關的部分。例如 - 從上面的命題中,海岸、學生、檔案是主語,而海灘、誠實和秘密是謂語。
範疇命題的型別
全稱命題 - 全稱命題是指完全包含或完全排除主語的命題。例如 - 沒有學生是聰明的。全稱命題進一步分為以下幾類 -
全稱肯定命題 - 當形式為所有 X 都是 Y時,稱為肯定命題。通常用字母A表示。
全稱否定命題 - 當形式為沒有 X 是 T時,稱為否定命題。用E表示。
特稱命題 - 它是部分顯示或部分排除主語但不完全排除主語的命題。例如,有些貓是棉花。它也分為以下型別 -
特稱肯定命題 - 像有些 X 是 U這樣的形式稱為特稱肯定命題。它們編碼為I。
特稱否定命題 - 像有些 T 不是 P這樣的形式,例如有些貓不是線圈,稱為特稱否定命題,編碼為O。
間接推理 - 結論是從兩個語句中得出的。例如 - “所有嘴唇都是線圈”和“所有球都是球棒”。所以結論將是“所有嘴唇都是線圈”。
直接推理 - 結論將僅從一個命題中得出。例如,如果陳述是“所有老師都是神”,那麼結論將是“有些老師是神”。
直接推理的兩種重要方法
這些方法包括轉換、反對等。
蘊含 - 假設給定“所有貓都是海灘”,那麼它表明結論“有些貓是海灘”是正確的。因此,如果給定的命題屬於 A 類,那麼它也表明 I 類結論必須為真。
轉換 - 它包括兩個步驟。
步驟 1 - 主語將轉換為謂語,反之亦然。
步驟 2 - 給定的命題將相應地改變。
例如 -
陳述 - 所有貓都是架子。所有包都是架子。有些錢包是包。
結論 -
1. 有些貓是包。
2. 有些架子是貓。
3. 有些架子是錢包。
A - 只有 1
B - 只有 2 和 3
C - 只有 1 和 2
D - 只有 1 和 3
解答 -
答案 - B 選項
尤拉提出了表示命題的圖解方法。根據四個命題,關係可以有四種表達方式。

型別 - A 代表“所有 X 都是 Y”,型別 - E 代表“沒有 X 是 Y”,型別 - I 代表“有些 A 是 B”,型別 - O 代表“有些 X 不是 Y”。
例如 -
陳述 -有些相機是筆記型電腦。
有些筆記型電腦是手機。
有些手機是平板電腦。
結論 -
I - 至少有些平板電腦是相機
II - 所有平板電腦都是筆記型電腦是有可能的
III - 沒有平板電腦是筆記型電腦
解答 -
圓形圖 -
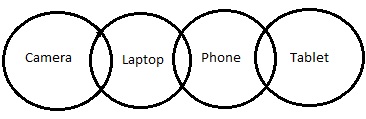
根據上圖,
結論 III 成立。但是陳述中提到了“可能性”這個詞。所以讓我們檢查一下可能性。
新的圖表將是 -
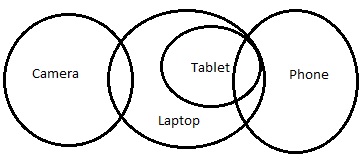
但在這種情況下,結論 III 不成立。結論 II 或結論 III 之一成立。
