推理 - 編碼二進位制數

底數為 2 的數稱為二進位制數。二進位制數由 0 和 1 的補碼組成。因此，編碼二進位制數包含兩個過程。一個是二進位制轉換為十進位制，另一個是十進位制轉換為二進位制。

十進位制數

要了解什麼是二進位制數，首先我們必須瞭解十進位制數。因此，十進位制數由十個數字組成（即 0、1、2、3、4、5、6、7、8、9）。任何十進位制系統都可以用這些數字表示。例如，一個數字序列是 2、4、6 和 8。我們以以下方式進行操作：

2468 = 2 × 10³ + 4 × 10² + 6 × 10¹ + 8 × 10⁰

= 2468

注意 - 在這種情況下，我們透過將序列的不同數字乘以 10 的冪並相加來獲得數字的值。這裡的 10 稱為基數或基。因此，在十進位制系統下，我們的基數是 10。

二進位制數

我們使用十個數字來表示十進位制數；就像我們只使用兩個數字來表示二進位制數一樣。任何數字都可以使用這兩個數字表示，即 0 和 1。

二進位制數的示例是 - 1101。這裡數字序列中存在 4 個數字 - 1、1、0、1。我們以以下方式獲得值。

1101 = 1 × 2³ + 1 × 2² + 0 × 2¹ + 1 × 2⁰

= 8 + 4 + 0 + 1 = 13

因此，二進位制數在十進位制系統中表示十三。可以透過將序列的不同數字乘以 2 的冪並相加來確定該值。

常規方法 - 在上面的示例中，我們看到要獲得任何二進位制數的值，我們使用以下規則：

最右邊的第一個數字乘以 2⁰ = 1

最右邊的第二個數字乘以 2¹ = 2

最右邊的第三個數字乘以 2² = 4

類似地，最右邊的第 n 個數字乘以 2ⁿ⁻¹

最後，將所有這些相加。

例如 - 將以下二進位制數轉換為十進位制數。

A - 1010

B - 1111

C - 100

D - 10000

解答 -

A - 1010 = 1 × 2³ + 0 × 2² + 1 × 2¹ + 0 × 2⁰

B - 1111 = 1 × 2³ + 1 × 2² + 1 × 2¹ + 1 × 2⁰

C - 100 = 1 × 2² + 0 × 2¹ + 0 × 2⁰

D - 10000 = 1 × 2⁴ + 0 × 2³ + 0 × 2² + 0 × 2¹ + 0 × 2⁰

更快捷的方法

步驟一 - 從給定數字的最右邊的數字開始，在每個數字下方寫 1、2、4、8、16、32……依此類推，當您向左移動時。

步驟二 - 忽略 0 下方的數字。將 1 下方的所有數字相加。

讓我們用這種方法解決示例 1。

A - 1010

我們將使用 1、2、4、8，因為這裡存在 4 個數字。

我們得到，

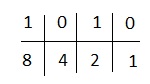
4 和 1 位於零的下方。我們忽略它們並新增其餘的。我們得到 8 + 2 = 10

像這樣我們可以解決其他數字。

十進位制數可以透過連續除法的方法轉換為二進位制。每次除法時，被除數都除以 2。記錄餘數，商成為下一個被除數，再次除以 2。重複此過程，直到不再可能進行除法。

例如 - 將 17 轉換為二進位制數 -

將 17 除以 2，直到不再可能進行除法。

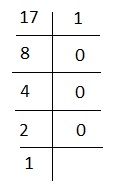
因此，17 的二進位制形式為 10001。

方向 (問題 1-4) - 研究以下問題並給出答案。

在某種程式碼中，0 的符號為 +，1 的符號為 #。沒有數字或符號大於 1。1 的符號的值每次向左移動一位時都會加倍。

‘0’ 表示為 +

‘1’ 表示為 #

‘2’ 表示為 #+

‘3’ 表示為 ##

‘4’ 表示為 #++，依此類推

1 - 以下哪個表示 11？

選項 -

A - #+##

B - +##+

C - ##++

D - #+#++

E - 以上皆非

答案 - 選項 A

解釋 - 要獲得 11 的等價物，我們使用連續除以 2 的方法。

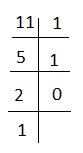
因此二進位制形式將為 10111。將 1 和 0 替換為 # 和 +，我們將得到 #+##。

2 - 以下哪個表示 8？

選項 -

A - ##++

B - +##+

C - ##++

D - ++##

E - 以上皆非

答案 - 選項 E

解釋 - 對於 8，我們有 -

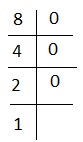
即 1000 或 #+++。正確選擇是 5。

3 - 以下哪個將由 ##+# 表示？

選項 -

A - 8

B - 11

C - 13

D - 12

E - 以上皆非

答案 - 選項 E

解釋 - ##+# = 1101 = 1 × 2³ + 1 × 2² + 0 × 2¹ + 1 × 2⁰ = 15

4 - 以下哪個數字將由 #+++# 表示？

選項 -

A - 22

B - 31

C - 14

D - 17

E - 以上皆非

答案 - 選項 D

解釋 - # + + + # = 10001

= 1 × 2⁴ + 0 × 2³ + 0 × 2² + 0 × 2¹ + 1 × 2⁰

= 16 + 1 = 17

二進位制系統以 2 為基數，十進位制系統以 10 為基數，三進位制系統以 3 為基數，而八進位制系統以 8 為基數。在三進位制的情況下，我們有三個數字來表示數字。這些是 0、1 和 2。在這種情況下，數字將透過乘以 3 的適當冪來轉換為十進位制。

例如 -

(12012)₃ = 1 × 3⁴ + 2 × 3³ + 0 × 3² + 1 × 3¹ + 2 × 3⁰ = (104)₃