推理 - 正方體和長方體
如今,幾乎每場競爭性考試都會出現一些基於“正方體和長方體”的問題。這些問題在各種競爭性考試中非常常見。
下面描述的方法既簡單又優雅。它們應該非常容易理解,並且只要稍微練習一下,你就能掌握它們。正方體是一個三維立體,具有 6 個面、12 條邊和 8 個角。正方體的所有邊都相等,所有面都是正方形。即一個具有 6 個面的立體圖形;每個面都是正方形,稱為正方體。如果六個面都是長方形,則稱為長方體。長方體也稱為直角平行六面體。
關於正方體和長方體的問題可能屬於以下型別。
型別 I
給出完整正方體的幾個檢視,你必須找到正方體的哪個部分正好位於特定部分的下方。
型別 II
給出展開的正方體,你必須預測它在摺疊成正方體後會是什麼樣子。
型別 III
一個正方體可能沒有或在其某些面上用相同顏色或不同顏色塗漆,然後將其切割成一定數量的相同小塊。然後問題形式為:“有多少個小正方體有 2 個面塗漆?”“有多少個小正方體只有一個面塗漆?”等等。
考試中出現兩種型別的題目。首先,給你一個完整正方體的幾個檢視,你必須說明正方體的哪個部分正好位於特定部分的下方。在另一種型別中,給你一個展開的正方體,你必須預測它在摺疊成正方體後會是什麼樣子。
例如 -
正方體的幾個面如下所示 -

哪個數字與 2 相對?
A - 1
B - 6
C - 5
D - 4
基本方法如下 -
型別 I
基本規則:相對面不能在一起;
每當我們看到一個正方體,只有三個面可見時,我們永遠無法看到兩個相對面在一起。有了所有這些規則,我們就可以輕鬆解決上面討論的問題型別。在上述問題中,我們需要找到特定面的相對面,我們可以排除那些在任何檢視中與 X 同時出現的那些面。因此,我們可以排除所有其他選擇,剩下的就是我們的答案。
此時,你應該再次通讀上一段,並確保你理解了這個概念。之後,你應該嘗試解決上述示例,看看是否能應用上面討論的概念。但是,如果你發現自己沒有完全理解這個概念,也沒關係。繼續閱讀本節內容。一旦你完成本節內容,事情就會變得清晰起來。牢記上述基本規則,你可以解決上述型別的問題。
對於這個問題,規則本身就足夠了。之後,你可以透過三個次要規則更快地解決它。
上述示例的解決方案 -
在給定的示例中,我們需要找到與 2 相對的面。現在在第一個圖形中,2 與 1 和 3 一起出現。這意味著 1 和 3 都不能與 2 相對。這意味著與 1 相對可以是 4 或 5 或 6。類似地,與 3 相對可以是 4 或 5 或 6。現在,看看第二個圖形。在這裡,3 和 1 與 5 同時出現。這意味著 5 既不是與 3 相對也不是與 1 相對。所以,這意味著 4 或 6 與 1 相對,另一個與 3 相對,所以 5 必須與 2 相對。因此 5 是正確答案。
一些更快的規則
現在你必須已經理解了解決此類問題的基本技巧。技巧是,你應該排除那些不可能的選擇。為此,你可以藉助基本規則,該規則指出,如果兩個面彼此相對,則它們不可能在一個正方體的檢視中同時出現。然而,在當今時間寶貴的競爭中,僅僅依靠概念是不夠的。你必須能夠快速解決問題。有一些次要規則可以用來解決問題。
規則 I - 我們稱那個需要找到其相對面的圖形為 X。假設在正方體的任何一個檢視中,X 與 Y 和 Z 一起出現。連同第三個圖形(例如 A),則 X 將與 A 相對。
例如,你需要找到與 2 相對的面。(這是我們的 X)。現在,2 在一個圖形中與 1 和 3 一起出現。(Y 和 Z)。此外,1 和 3 在另一個圖形中一起出現,與 5 一起出現。(即 A)。因此,2 必須與 5 相對。
規則 II - 我們需要找到‘X’的相對面。假設在正方體的任何一個檢視中,X 與 Y 和 Z 一起出現。現在,假設 Y 和 Z 在任何其他檢視中都不一起出現,但它們在兩個或多個不同的檢視中分別出現。那麼,Y 和 Z 分別出現的兩個或多個不同檢視之間的公共圖形將是與 X 相對的圖形。
規則 III - 我們稱需要找到其相對面的圖形為 X。現在,假設 X 出現在兩個檢視中,並且在這兩個檢視中,可以看到四個不同的圖形與 X 一起出現。那麼,在這兩個檢視中沒有與 X 一起出現的唯一圖形必須與 X 相對。
總結 - 你必須牢記基本規則,然後應用三個次要規則來快速回答。整個方法可以透過以下圖表進行總結。
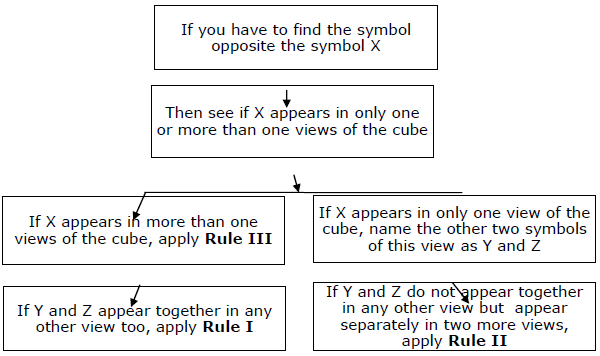
型別 II
在這種型別中,我們使用基本規則。此規則幫助我們排除那些在單個檢視中顯示相對面的組合。因此,如果我們知道如何透過檢視“展開的正方體”來確定哪些面彼此相對,它將導致排除一個選擇。為此,有一個非常簡單的規則,透過該規則,你只需檢視展開的正方體,就可以透過檢視它來判斷哪些面彼此相對。
規則如下;
第三個相對規則 -
當你想找出某個面的相對面(例如 X)時,在圖 I、II、III 中;給出一個展開的正方體。我們需要找到當正方體閉合時哪些面彼此相對。
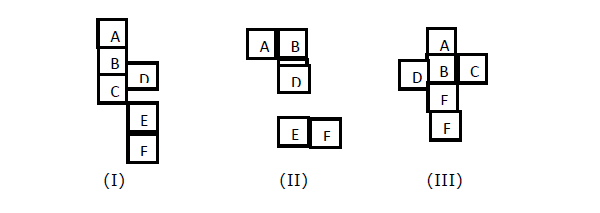
解釋 -
在圖 (I) 中,A 的第三個圖形是 C。所以 A 與 C 相對。所以,D 和 F 將彼此相對。B 和 E 將彼此相對。
在圖 (II) 中,B 是 D 的第三個圖形,所以 B 將與 D 相對。類似地,C 將與 E 相對,A 將與 F 相對。
在圖 (III) 中,A 與 E 相對,B 與 F 相對。因此,C 與 D 相對。
解決問題的步驟
我們現在可以解決此型別的題目。我們知道如何透過檢視展開的正方體來找到相對面。我們也知道,在正方體的任何檢視中,相對面都不能在一起。因此,結合這兩個規則,我們可以輕鬆解決問題。
總結
至此,關於如何解決型別 II 問題的討論就完成了。你必須使用“第三個相對規則”來確定哪些面彼此相對。下圖將提供有關此方法的完整資訊。
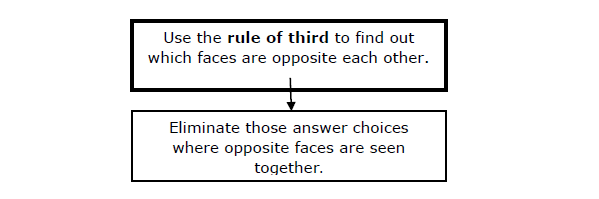
型別 III
正方體的計數(當塗漆的實心正方體被切割時);
在上一節中,我們討論了查詢正方體相對面的問題。還有另一種與正方體相關的問題,其中一個較大的正方體在其不同側面塗有不同的顏色,被分成幾個較小的正方體,你必須找到只有一個側面塗漆或兩個側面塗漆的正方體的數量。
此問題的格式 -
示例 -
一個正方體的側面塗有三種顏色:綠色、藍色和紅色,每種顏色都塗在正方體的相對面上。現在,將正方體分成 64 個大小相等的小正方體。根據這些資訊,回答以下問題 -
1. 有多少個小正方體有兩個面塗漆,其餘面未塗漆?
A - 18
B - 20
C - 22
D - 24
2. 有多少個小正方體只有一個面塗漆(僅為綠色或藍色)?
A - 4
B - 24
C - 16
D - 12
3. 有多少個小正方體沒有側面塗漆?
A - 0
B - 8
C - 12
D - 64
