數字訊號處理 - Z 變換性質

---

---

本章我們將瞭解 Z 變換的基本性質。

線性性

它指出，當兩個或多個單獨的離散訊號乘以常數時，它們的 Z 變換也將乘以相同的常數。

數學表示式為：

$$a_1x_1(n)+a_2x_2(n) = a_1X_1(z)+a_2X_2(z)$$

證明 - 我們知道：

$$X(Z) = \sum_{n=-\infty}^\infty x(n)Z^{-n}$$

$= \sum_{n=-\infty}^\infty (a_1x_1(n)+a_2x_2(n))Z^{-n}$

$= a_1\sum_{n = -\infty}^\infty x_1(n)Z^{-n}+a_2\sum_{n = -\infty}^\infty x_2(n)Z^{-n}$

$= a_1X_1(z)+a_2X_2(z)$ (證畢)

此處，收斂域為 $ROC_1\bigcap ROC_2$。

時間移位

時間移位特性描述了離散訊號在時域的變化如何影響 Z 域，可以寫成：

$$x(n-n_0)\longleftrightarrow X(Z)Z^{-n}$$

或 $x(n-1)\longleftrightarrow Z^{-1}X(Z)$

證明 -

設 $y(P) = X(P-K)$

$Y(z) = \sum_{p = -\infty}^\infty y(p)Z^{-p}$

$= \sum_{p = -\infty}^\infty (x(p-k))Z^{-p}$

設 s = p-k

$= \sum_{s = -\infty}^\infty x(s)Z^{-(s+k)}$

$= \sum_{s = -\infty}^\infty x(s)Z^{-s}Z^{-k}$

$= Z^{-k}[\sum_{s=-\infty}^\infty x(m)Z^{-s}]$

$= Z^{-k}X(Z)$ (證畢)

此處，收斂域可以寫成 Z = 0 (p>0) 或 Z = ∞(p<0)

示例

U(n) 和 U(n-1) 可以繪製如下

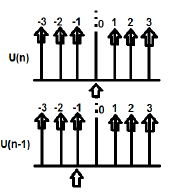
U(n) 的 Z 變換可以寫成：

$\sum_{n = -\infty}^\infty [U(n)]Z^{-n} = 1$

U(n-1) 的 Z 變換可以寫成：

$\sum_{n = -\infty}^\infty [U(n-1)]Z^{-n} = Z^{-1}$

所以這裡 $x(n-n_0) = Z^{-n_0}X(Z)$ (證畢)

時間尺度變換

時間尺度變換特性告訴我們，當離散訊號的時間進行尺度變換時，其 Z 域將如何變化，可以寫成：

$$a^nx(n) \longleftrightarrow X(a^{-1}Z)$$

證明 -

設 $y(p) = a^{p}x(p)$

$Y(P) = \sum_{p=-\infty}^\infty y(p)Z^{-p}$

$= \sum_{p=-\infty}^\infty a^px(p)Z^{-p}$

$= \sum_{p=-\infty}^\infty x(p)[a^{-1}Z]^{-p}$

$= X(a^{-1}Z)$(證畢)

收斂域：= Mod(ar1) < Mod(Z) < Mod(ar2) 其中 Mod = 模

示例

讓我們使用時間尺度變換特性確定 $x(n) = a^n \cos \omega n$ 的 Z 變換。

解 -

我們已經知道訊號 $\cos (\omega n)$ 的 Z 變換為：

$$ \sum_{n=-\infty}^\infty(\cos \omega n)Z^{-n} = (Z^2-Z \cos \omega)/(Z^2-2Z\cos \omega +1) $$

現在，應用時間尺度變換特性，$a^n \cos \omega n$ 的 Z 變換可以寫成：

$\sum_{n=-\infty}^\infty(a^n\cos \omega n)Z^{-n} = X(a^{-1}Z)$

$= [(a^{-1}Z)^2-(a^{-1}Z \cos \omega n)]/((a^{-1}Z)^2-2(a^{-1}Z \cos \omega n)+1)$

$= Z(Z-a \cos \omega)/(Z^2-2az \cos \omega+a^2)$

連續微分

連續微分特性表明，當我們對時域中的離散訊號關於時間進行微分時，將進行 Z 變換。如下所示。

$$\frac{dx(n)}{dn} = (1-Z^{-1})X(Z)$$

證明 -

考慮方程的左邊 - $\frac{dx(n)}{dn}$

$$= \frac{[x(n)-x(n-1)]}{[n-(n-1)]}$$

$= x(n)-X(n-1)$

$= x(Z)-Z^{-1}x(Z)$

$= (1-Z^{-1})x(Z)$ (證畢)

收斂域：R1< Mod (Z) <R2

示例

讓我們找到由 $x(n) = n^2u(n)$ 給出的訊號的 Z 變換

根據性質，我們可以寫成

$Zz[nU(n)] = -Z\frac{dZ[U(n)]}{dz}$

$= -Z\frac{d[\frac{Z}{Z-1}]}{dZ}$

$= Z/((Z-1)^2$

$= y(設)$

現在，Z[n.y] 可以透過再次應用該性質找到：

$Z(n,y) = -Z\frac{dy}{dz}$

$= -Z\frac{d[Z/(Z-1)^3]}{dz}$

$= Z(Z+1)/(Z-1)^2$

卷積

這描述了當離散訊號形式發生卷積時系統的 Z 域變化，可以寫成：

$x_1(n)*x_2(n) \longleftrightarrow X_1(Z).X_2(Z)$

證明 -

$X(Z) = \sum_{n = -\infty}^\infty x(n)Z^{-n}$

$= \sum_{n=-\infty}^\infty[\sum_{k = -\infty}^\infty x_1(k)x_2(n-k)]Z^{-n}$

$= \sum_{k = -\infty}^\infty x_1(k)[\sum_n^\infty x_2(n-k)Z^{-n}]$

$= \sum_{k = -\infty}^\infty x_1(k)[\sum_{n = -\infty}^\infty x_2(n-k)Z^{-(n-k)}Z^{-k}]$

設 n-k = l，則上述方程可以寫成：

$X(Z) = \sum_{k = -\infty}^\infty x_1(k)[Z^{-k}\sum_{l=-\infty}^\infty x_2(l)Z^{-l}]$

$= \sum_{k = -\infty}^\infty x_1(k)X_2(Z)Z^{-k}$

$= X_2(Z)\sum_{k = -\infty}^\infty x_1(Z)Z^{-k}$

$= X_1(Z).X_2(Z)$ (證畢)

收斂域：$ROC_1 \bigcap ROC_2$

示例

讓我們找到由兩個訊號給出的卷積

$x_1(n) = \lbrace 3,-2,2\rbrace$ ...(等式 1)

$x_2(n) = \lbrace 2,0\leq 4\quad and\quad 0\quad elsewhere\rbrace$ ...(等式 2)

第一個方程的 Z 變換可以寫成：

$\sum_{n = -\infty}^\infty x_1(n)Z^{-n}$

$= 3-2Z^{-1}+2Z^{-2}$

第二個訊號的 Z 變換可以寫成：

$\sum_{n = -\infty}^\infty x_2(n)Z^{-n}$

$= 2+2Z^{-1}+2Z^{-2}+2Z^{-3}+2Z^{-4}$

因此，上述兩個訊號的卷積由下式給出：

$X(Z) = [x_1(Z)^*x_2(Z)]$

$= [3-2Z^{-1}+2Z^{-2}]\times [2+2Z^{-1}+2Z^{-2}+2Z^{-3}+2Z^{-4}]$

$= 6+2Z^{-1}+6Z^{-2}+6Z^{-3}+...\quad...\quad...$

進行逆 Z 變換，我們得到：

$x(n) = \lbrace 6,2,6,6,6,0,4\rbrace$

初始值定理

如果 x(n) 是一個因果序列，其 Z 變換為 X(z)，則初始值定理可以寫成：

$X(n)(at\quad n = 0) = \lim_{z \to \infty} X(z)$

證明 - 我們知道：

$X(Z) = \sum_{n = 0} ^\infty x(n)Z^{-n}$

展開上述級數，我們得到：

$= X(0)Z^0+X(1)Z^{-1}+X(2)Z^{-2}+...\quad...$

$= X(0)\times 1+X(1)Z^{-1}+X(2)Z^{-2}+...\quad...$

在上述情況下，如果 Z → ∞，則 $Z^{-n}\rightarrow 0$（因為 n>0）

因此，我們可以說：

$\lim_{z \to \infty}X(z) = X(0)$ (證畢)

最終值定理

最終值定理指出，如果訊號的 Z 變換表示為 X(Z)，並且極點都在單位圓內，則其最終值表示為 x(n) 或 X(∞)，可以寫成：

$X(\infty) = \lim_{n \to \infty}X(n) = \lim_{z \to 1}[X(Z)(1-Z^{-1})]$

條件 -

• 僅適用於因果系統。
• $X(Z)(1-Z^{-1})$ 在 Z 平面上應該具有單位圓內的極點。

證明 - 我們知道

$Z^+[x(n+1)-x(n)] = \lim_{k \to \infty}\sum_{n=0}^kZ^{-n}[x(n+1)-x(n)]$

$\Rightarrow Z^+[x(n+1)]-Z^+[x(n)] = \lim_{k \to \infty}\sum_{n=0}^kZ^{-n}[x(n+1)-x(n)]$

$\Rightarrow Z[X(Z)^+-x(0)]-X(Z)^+ = \lim_{k \to \infty}\sum_{n = 0}^kZ^{-n}[x(n+1)-x(n)]$

這裡，我們可以應用單邊 Z 變換的高階性質。因此，上述方程可以改寫為：

$Z^+[x(n+1)] = Z[X(2)^+-x(0)Z^0] = Z[X(Z)^+-x(0)]$

現在將 z = 1 代入上述方程，我們可以展開上述方程：

$\lim_{k \to \infty}{[x(1)-x(0)+x(6)-x(1)+x(3)-x(2)+...\quad...\quad...+x(x+1)-x(k)]}$

這可以表示為：

$X(\infty) = \lim_{n \to \infty}X(n) = \lim_{z \to 1}[X(Z)(1-Z^{-1})]$(證畢)

示例

讓我們找到 x(n) 的初始值和最終值，其訊號由下式給出

$X(Z) = 2+3Z^{-1}+4Z^{-2}$

解 - 讓我們首先透過應用定理找到訊號的初始值

$x(0) = \lim_{z \to \infty}X(Z)$

$= \lim_{z \to \infty}[2+3Z^{-1}+4Z^{-2}]$

$= 2+(\frac{3}{\infty})+(\frac{4}{\infty}) = 2$

現在讓我們透過應用定理找到訊號的最終值

$x(\infty) = \lim_{z \to \infty}[(1-Z^{-1})X(Z)]$

$= \lim_{z \to \infty}[(1-Z^{-1})(2+3Z^{-1}+4Z^{-2})]$

$= \lim_{z \to \infty}[2+Z^{-1}+Z^{-2}-4Z^{-3}]$

$= 2+1+1-4 = 0$

Z 變換的其他一些性質列在下面 -

頻域微分

它給出當離散訊號關於時間進行微分時訊號的 Z 域變化。

$nx(n)\longleftrightarrow -Z\frac{dX(z)}{dz}$

其收斂域可以寫成：

$r_2< Mod(Z)< r_1$

示例

讓我們透過頻域微分找到 x(n) 的值，其在 Z 域中的離散訊號由 $x(n)\longleftrightarrow X(Z) = log(1+aZ^{-1})$ 給出

根據性質，我們可以寫成

$nx(n)\longleftrightarrow -Z\frac{dx(Z)}{dz}$

$= -Z[\frac{-aZ^{-2}}{1+aZ^{-1}}]$

$= (aZ^{-1})/(1+aZ^{-1})$

$= 1-1/(1+aZ^{-1})$

$nx(n) = \delta(n)-(-a)^nu(n)$

$\Rightarrow x(n) = 1/n[\delta(n)-(-a)^nu(n)]$

時域相乘

它給出當在離散訊號級別進行乘法運算時訊號的 Z 域變化。

$x_1(n).x_2(n)\longleftrightarrow(\frac{1}{2\Pi j})[X1(Z)*X2(Z)]$

時域共軛

這描述了 Z 域中共軛離散訊號的表示。

$X^*(n)\longleftrightarrow X^*(Z^*)$