數字訊號處理 - 基本離散時間訊號

---

---

我們已經瞭解瞭如何在連續時間域表示基本訊號。讓我們看看如何在離散時間域表示基本訊號。

單位脈衝序列

在離散時間域中表示為 δ(n)，其定義如下：

$$\delta(n)=\begin{cases}1, & for \quad n=0\\0, & Otherwise\end{cases}$$

單位階躍訊號

離散時間單位階躍訊號定義如下：

$$U(n)=\begin{cases}1, & for \quad n\geq0\\0, & for \quad n<0\end{cases}$$

上圖顯示了離散階躍函式的圖形表示。

單位斜坡函式

離散單位斜坡函式可以定義為：

$$r(n)=\begin{cases}n, & for \quad n\geq0\\0, & for \quad n<0\end{cases}$$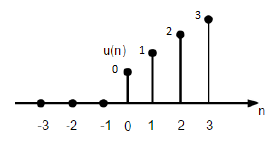

上圖顯示了離散斜坡訊號的圖形表示。

拋物線函式

離散單位拋物線函式表示為 p(n)，其定義如下：

$$p(n) = \begin{cases}\frac{n^{2}}{2} ,& for \quad n\geq0\\0, & for \quad n<0\end{cases}$$

用單位階躍函式表示為：

$$P(n) = \frac{n^{2}}{2}U(n)$$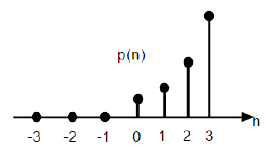

上圖顯示了拋物線序列的圖形表示。

正弦訊號

所有連續時間訊號都是週期性的。離散時間正弦序列可能是週期性的，也可能不是週期性的。這取決於 ω 的值。對於離散時間訊號要成為週期性的，角頻率 ω 必須是 2π 的有理數倍。

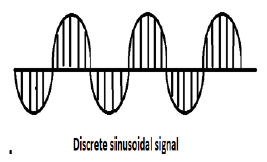
上圖顯示了一個離散正弦訊號。

離散正弦訊號可以表示為以下格式：

$$x(n) = A\sin(\omega n + \phi)$$

這裡 A、ω 和 φ 具有其通常的含義，n 是整數。離散正弦訊號的週期由下式給出：

$$N =\frac{2\pi m}{\omega}$$

其中，N 和 m 是整數。