
- 數字訊號處理教程
- 數字訊號處理 - 首頁
- 數字訊號處理 - 訊號定義
- 數字訊號處理 - 基本連續時間訊號
- 數字訊號處理 - 基本離散時間訊號
- 數字訊號處理 - 連續時間訊號分類
- 數字訊號處理 - 離散時間訊號分類
- 數字訊號處理 - 其他訊號
- 基本系統特性
- 數字訊號處理 - 靜態系統
- 數字訊號處理 - 動態系統
- 數字訊號處理 - 因果系統
- 數字訊號處理 - 非因果系統
- 數字訊號處理 - 反因果系統
- 數字訊號處理 - 線性系統
- 數字訊號處理 - 非線性系統
- 數字訊號處理 - 時不變系統
- 數字訊號處理 - 時變系統
- 數字訊號處理 - 穩定系統
- 數字訊號處理 - 不穩定系統
- 數字訊號處理 - 例題解析
- 數字訊號處理資源
- 數字訊號處理 - 快速指南
- 數字訊號處理 - 有用資源
- 數字訊號處理 - 討論
數字訊號處理 - 訊號微分運算
對訊號進行的兩個非常重要的運算分別是微分和積分。
微分
任何訊號 x(t) 的微分表示該訊號關於時間的斜率。數學上表示為:
$$x(t)\rightarrow \frac{dx(t)}{dt}$$在運放微分電路中,這種方法非常有用。我們可以很容易地透過圖形方法對訊號進行微分,而不是使用公式。然而,條件是訊號必須是矩形或三角形型別的,這在大多數情況下都是如此。
| 原始訊號 | 微分後的訊號 |
|---|---|
| 斜坡訊號 | 階躍訊號 |
| 階躍訊號 | 衝激訊號 |
| 衝激訊號 | 1 |
上表說明了訊號微分後的情況。例如,斜坡訊號微分後變成階躍訊號。類似地,單位階躍訊號變成衝激訊號。
示例
假設給定的訊號為 $x(t) = 4[r(t)-r(t-2)]$。繪製該訊號時,它看起來像下面圖形左側所示的那樣。現在,我們的目標是對給定的訊號進行微分。
首先,我們將開始對給定的方程進行微分。我們知道斜坡訊號微分後得到單位階躍訊號。
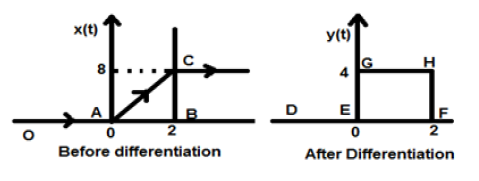
因此,我們的結果訊號 y(t) 可以寫成:
$y(t) = \frac{dx(t)}{dt}$
$= \frac{d4[r(t)-r(t-2)]}{dt}$
$= 4[u(t)-u(t-2)]$
現在,最終繪製了該訊號,如上圖右側所示。
廣告