數字訊號處理 - 訊號定義

定義

任何攜帶資訊的都可以稱為訊號。它也可以定義為隨時間、溫度、壓力或任何自變數（如語音訊號或影片訊號）變化的物理量。

訊號的特徵（幅度、形狀、相位、頻率等）發生變化的操作過程稱為訊號處理。

注意 - 任何干擾主訊號的非期望訊號稱為噪聲。因此，噪聲也是訊號，但是非期望的。

根據訊號的表示和處理方式，可以將其分為不同的類別，下面將詳細討論。

連續時間訊號沿時間連續體定義，因此由連續的獨立變量表示。連續時間訊號通常稱為模擬訊號。

這種型別的訊號在幅度和時間上都表現出連續性。它們在每個時刻都會有值。正弦和餘弦函式是連續時間訊號的最佳示例。

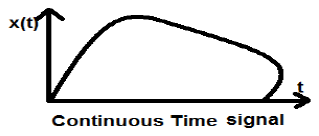
上面顯示的訊號是連續時間訊號的一個例子，因為我們可以在每個時刻獲得訊號的值。

在離散時間定義的訊號稱為離散訊號。因此，每個獨立變數都有不同的值。因此，它們表示為數字序列。

雖然語音和影片訊號都可以在連續時間和離散時間格式下表示；但在某些情況下，它們是相同的。幅度也表現出離散特徵。數字訊號是此類訊號的完美示例；其幅度和時間都是離散的。

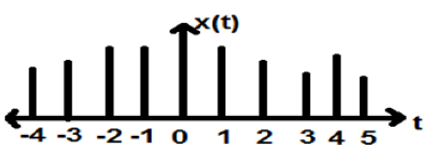
上圖描繪了離散訊號在一段時間內的離散幅度特徵。在數學上，這些型別的訊號可以公式化為；

$$x = \left \{ x\left [ n \right ] \right \},\quad -\infty < n< \infty$$

其中，n 是整數。

它是一個數字序列 x，其中序列中的第 n 個數字表示為 x[n]。

列印頁面