數字訊號處理 - 計算機輔助設計

---

---

FIR濾波器在計算機輔助設計濾波器中非常有用。讓我們舉個例子看看它是如何工作的。下面是所需濾波器的圖形。

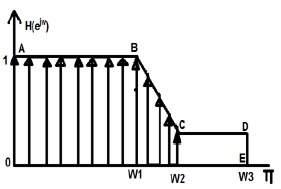
在進行計算機設計時，我們將整個連續圖形分解成離散值。在一定的範圍內，我們將它分成64、256或512（等等）個具有離散幅度的部分。

在上面的例子中，我們取了-π到+π之間的範圍。我們將其分成了256個部分。這些點可以表示為H(0)、H(1)、…直到H(256)。在這裡，我們應用IDFT演算法，這將為我們提供線性相位特性。

有時，我們可能對某種特定階數的濾波器感興趣。假設我們想透過9階濾波器實現上述設計。因此，我們將濾波器值取為h0、h1、h2…h9。數學上，它可以表示如下

$$H(e^{j\omega}) = h_0+h_1e^{-j\omega}+h_2e^{-2j\omega}+.....+h_9e^{-9j\omega}$$

在存在大量錯位的地方，我們取最大點數。

例如，在上圖中，點B和C之間有一個突然的斜率下降。因此，我們嘗試在此點取更多離散值，但在點C和D之間有一個恆定的斜率。在那裡，我們取較少的離散值。

為了設計上述濾波器，我們透過以下最小化過程：

$H(e^{j\omega1}) = h_0+h_1e^{-j\omega1}+h_2e^{-2j\omega1}+.....+h_9e^{-9j\omega1}$

$H(e^{j\omega2}) = h_0+h_1e^{-j\omega2}+h_2e^{-2j\omega2}+.....+h_9e^{-9j\omega2}$

類似地，

$(e^{j\omega1000}) = h_0+h_1eH^{-j\omega1000}h_2e^{-2j\omega1000}+.....+h_9+e^{-9j\omega1000}$

將上述方程表示為矩陣形式，我們有：

$$\begin{bmatrix}H(e^{j\omega_1})\\.\\.\\H(e^{j\omega_{1000}}) \end{bmatrix} = \begin{bmatrix}e^{-j\omega_1} & ... & e^{-j9\omega_1} \\. & & . \\. & & . \\e^{-j\omega_{1000}} &... & e^{j9\omega_{1000}} \end{bmatrix}\begin{bmatrix}h_0\\.\\.\\h_9\end{bmatrix}$$

讓我們將1000×1矩陣作為B，1000×9矩陣作為A，9×1矩陣作為$\hat{h}$。

因此，為了求解上述矩陣，我們將寫

$\hat{h} = [A^TA]^{-1}A^{T}B$

$= [A^{*T}A]^{-1}A^{*T}B$

其中A^*表示矩陣A的複共軛。