數字訊號處理 - 時不變系統

對於時不變系統，輸出和輸入應該延時相同的單位時間。對於時不變系統，輸入中的任何延時都必須反映在輸出中。

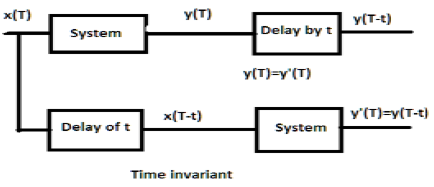
示例

a) $y(T) = x(2T)$

如果上述表示式首先透過系統，然後透過時間延遲（如圖上半部分所示）；則輸出將變為$x(2T-2t)$。現在，相同的表示式首先透過時間延遲，然後透過系統（如圖下半部分所示）。輸出將變為$x(2T-t)$。

因此，該系統不是時不變系統。

b) $y(T) = \sin [x(T)]$

如果訊號首先透過系統，然後透過時間延遲過程，則輸出為$\sin x(T-t)$。類似地，如果系統首先透過時間延遲，然後透過系統，則輸出將為$\sin x(T-t)$。我們可以清楚地看到，這兩個輸出是相同的。因此，該系統是時不變的。