數字訊號處理 - 基本連續時間訊號

---

---

為了測試系統，通常使用標準或基本訊號。這些訊號是許多複雜訊號的基本組成部分。因此，它們在訊號和系統研究中扮演著非常重要的角色。

單位衝激訊號或狄拉克函式

滿足條件$\delta(t) = \lim_{\epsilon \to 0} x(t)$的訊號稱為單位衝激訊號。該訊號在t=0時趨於無窮大，在t≠0時趨於零，其曲線下的面積始終等於1。除了t=0點外，狄拉克函式在其他任何地方的幅度都為零。

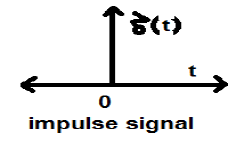
單位衝激訊號的特性

• δ(t)是偶函式。
• δ(t)是非能量非功率(NENP)訊號。
• 單位衝激訊號的面積可以寫成：
$$A = \int_{-\infty}^{\infty} \delta (t)dt = \int_{-\infty}^{\infty} \lim_{\epsilon \to 0} x(t) dt = \lim_{\epsilon \to 0} \int_{-\infty}^{\infty} x(t)dt = 1$$
• 訊號的權重或強度可以寫成：
$$y(t) = A\delta (t)$$
• 加權衝激訊號的面積可以寫成：
$$y (t) = \int_{-\infty}^{\infty} y (t)dt = \int_{-\infty}^{\infty} A\delta (t) = A[\int_{-\infty}^{\infty} \delta (t)dt ] = A$$

單位階躍訊號

滿足以下兩個條件的訊號：

• $U(t) = 1(當\quad t \geq 0)$且
• $U(t) = 0 (當\quad t < 0)$

稱為單位階躍訊號。

它具有在t=0處顯示不連續性的特性。在不連續點，訊號值由訊號值平均值給出。該訊號是在不連續點之前和之後取的（根據吉布斯現象）。

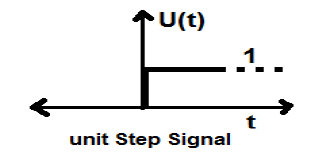
如果我們將一個階躍訊號新增到另一個經過時間縮放的階躍訊號，則結果將為1.它是一種功率型訊號，功率值為0.5。均方根(RMS)值為0.707，平均值也為0.5。

斜坡訊號

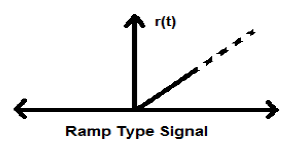
階躍訊號的積分產生斜坡訊號。它用r(t)表示。斜坡訊號也滿足條件$r(t) = \int_{-\infty}^{t} U(t)dt = tU(t)$。它是非能量非功率(NENP)型訊號。

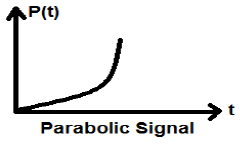
拋物線訊號

斜坡訊號的積分導致拋物線訊號。它用p(t)表示。拋物線訊號也滿足條件$p(t) = \int_{-\infty}^{t} r(t)dt = (t^{2}/2)U(t)$。它是非能量非功率(NENP)型訊號。

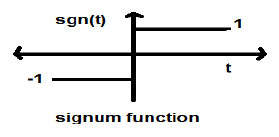
符號函式

此函式表示為

$$sgn(t) = \begin{cases}1 & 當\quad t >0\\-1 & 當\quad t<0\end{cases}$$

它是一種功率型訊號。其功率值和均方根(RMS)值均為1。符號函式的平均值為零。

Sinc函式

它也是正弦函式，寫成：

$$SinC(t) = \frac{Sin\Pi t}{\Pi t} = Sa(\Pi t)$$

Sinc函式的特性

• 它是一種能量型訊號。

• $Sinc(0) = \lim_{t \to 0}\frac{\sin \Pi t}{\Pi t} = 1$

• $Sinc(\infty) = \lim_{t \to \infty}\frac{\sin \Pi \infty}{\Pi \infty} = 0$（sinπ∞的範圍在-1到+1之間，但任何數除以無窮大都等於零）

• 如果$ \sin c(t) = 0 => \sin \Pi t = 0$

  $\Rightarrow \Pi t = n\Pi$

  $\Rightarrow t = n (n \neq 0)$

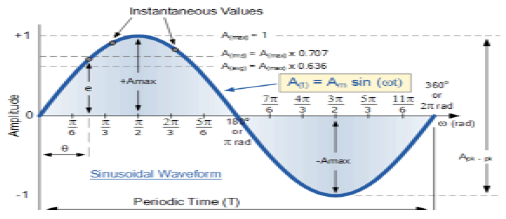
正弦訊號

連續性質的訊號稱為連續訊號。正弦訊號的一般形式為

$$x(t) = A\sin (\omega t + \phi )$$

這裡，

A = 訊號的幅度

ω = 訊號的角頻率（以弧度為單位測量）

φ = 訊號的相位角（以弧度為單位測量）

該訊號傾向於在一定時間段後重復自身，因此稱為週期訊號。訊號的週期為：

$$T = \frac{2\pi }{\omega }$$

正弦訊號的示意圖如下所示。

矩形函式

如果訊號滿足以下條件，則稱為矩形函式型別：

$$\pi(\frac{t}{\tau}) = \begin{cases}1, & 當\quad |t|\leq \frac{\tau}{2}\\0, & 其他情況\end{cases}$$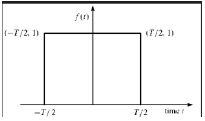

由於關於Y軸對稱，因此該訊號稱為偶函式。

三角脈衝訊號

任何滿足以下條件的訊號都稱為三角訊號。

$$\Delta(\frac{t}{\tau}) = \begin{cases}1-(\frac{2|t|}{\tau}) & 當|t|<\frac{\tau}{2}\\0 & 當|t|>\frac{\tau}{2}\end{cases}$$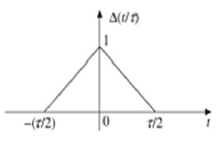

該訊號關於Y軸對稱。因此，它也稱為偶函式。