
- 數字訊號處理教程
- 數字訊號處理 - 首頁
- 數字訊號處理 - 訊號定義
- 數字訊號處理 - 基本連續時間訊號
- 數字訊號處理 - 基本離散時間訊號
- 數字訊號處理 - 連續時間訊號分類
- 數字訊號處理 - 離散時間訊號分類
- 數字訊號處理 - 其他訊號
- 基本系統特性
- 數字訊號處理 - 靜態系統
- 數字訊號處理 - 動態系統
- 數字訊號處理 - 因果系統
- 數字訊號處理 - 非因果系統
- 數字訊號處理 - 反因果系統
- 數字訊號處理 - 線性系統
- 數字訊號處理 - 非線性系統
- 數字訊號處理 - 時不變系統
- 數字訊號處理 - 時變系統
- 數字訊號處理 - 穩定系統
- 數字訊號處理 - 不穩定系統
- 數字訊號處理 - 例題解析
- 數字訊號處理資源
- 數字訊號處理 - 快速指南
- 數字訊號處理 - 有用資源
- 數字訊號處理 - 討論
數字訊號處理 - 訊號縮放運算
訊號縮放是指將一個常數乘以訊號的時間或幅度。
時間縮放
如果將一個常數乘以時間軸,則稱為時間縮放。這可以用數學方式表示為:
$x(t) \rightarrow y(t) = x(\alpha t)$ 或 $x(\frac{t}{\alpha})$; 其中 α ≠ 0
因此,y軸保持不變,x軸的幅度根據常數的符號(正或負)而減小或增大。因此,縮放也可以分為以下兩類。
時間壓縮
當alpha大於零時,訊號的幅度被alpha除,而Y軸的值保持不變。這被稱為時間壓縮。
示例
讓我們考慮一個訊號x(t),如下圖所示。讓我們取alpha的值為2。所以,y(t)將是x(2t),如下圖所示。
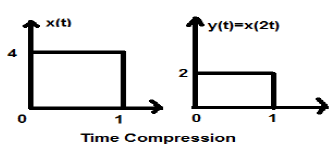
從上圖可以清楚地看出,y軸的時間幅度保持不變,但x軸的幅度從4減小到2。因此,這是一個時間壓縮的情況。
時間擴充套件
當時間除以常數alpha時,訊號的Y軸幅度乘以alpha倍,而X軸幅度保持不變。因此,這稱為時間擴充套件型訊號。
示例
讓我們考慮一個幅度為1的方波訊號x(t)。當我們將其時間縮放一個常數3,使得$x(t) \rightarrow y(t) \rightarrow x(\frac{t}{3})$時,訊號的幅度將乘以3倍,如下圖所示。
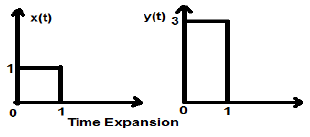
幅度縮放
將一個常數乘以訊號的幅度會導致幅度縮放。根據常數的符號,它可以是幅度縮放或衰減。讓我們考慮一個方波訊號x(t) = Π(t/4)。
假設我們定義另一個函式y(t) = 2 Π(t/4)。在這種情況下,y軸的值將加倍,而時間軸的值保持不變。如下圖所示。
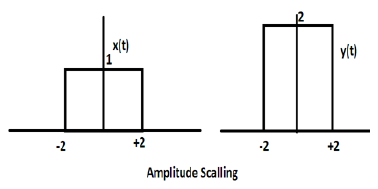
考慮另一個定義為z(t)的方波函式,其中z(t) = 0.5 Π(t/4)。這裡,函式z(t)的幅度將是x(t)的一半,即時間軸保持不變,幅度軸將減半。如下圖所示。
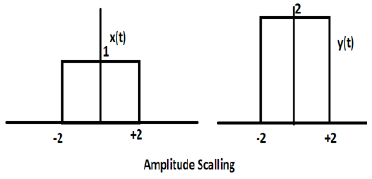
廣告