數字訊號處理 - 快速傅立葉變換

---

---

在之前的 DFT 方法中，我們看到計算部分過於冗長。我們需要減少它。這可以透過 FFT 或快速傅立葉變換來實現。所以，我們可以說 FFT 不過是離散傅立葉變換的演算法化計算，其中計算量將會減少。

FFT 的主要優點在於，透過它我們可以設計 FIR 濾波器。從數學上講，FFT 可以寫成如下形式：

$$x[K] = \displaystyle\sum\limits_{n = 0}^{N-1}x[n]W_N^{nk}$$

讓我們舉個例子來更好地理解它。我們考慮了從 $x_0\quad 到\quad x_7$ 的八個點。我們將偶數項放在一組，奇數項放在另一組。上面提到的示意圖如下所示：

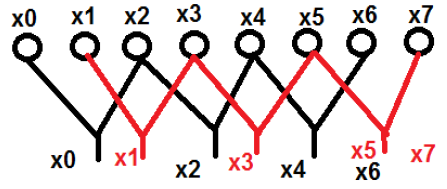
這裡，點 x₀、x₂、x₄ 和 x₆ 被歸為一類，類似地，點 x₁、x₃、x₅ 和 x₇ 被歸為另一類。現在，我們可以進一步將它們分成兩組，並繼續進行計算。現在，讓我們看看這些進一步分成兩組是如何幫助計算的。

$x[k] = \displaystyle\sum\limits_{r = 0}^{\frac{N}{2}-1}x[2r]W_N^{2rk}+\displaystyle\sum\limits_{r = 0}^{\frac{N}{2}-1}x[2r+1]W_N^{(2r+1)k}$

$= \sum_{r = 0}^{\frac{N}{2}-1}x[2r]W_{N/2}^{rk}+\sum_{r = 0}^{\frac{N}{2}-1}x[2r+1]W_{N/2}^{rk}\times W_N^k$

$= G[k]+H[k]\times W_N^k$

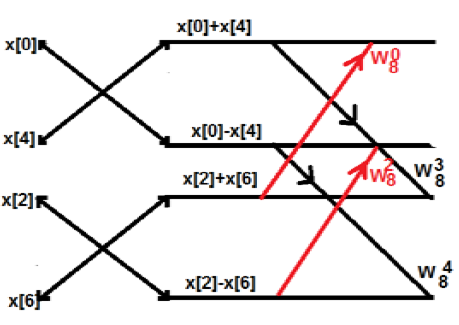
最初，我們取了一個八點序列，但後來我們將其分成兩部分 G[k] 和 H[k]。G[k] 代表偶數部分，而 H[k] 代表奇數部分。如果我們想透過圖表來實現它，那麼它可以顯示如下：

從上圖可以看出

$W_8^4 = -1$

$W_8^5 = -W_8^1$

$W_8^6 = -W_8^2$

$W_8^7 = -W_8^3$

類似地，最終值可以寫成如下形式：

$G[0]-H[0] = x[4]$

$G[1]-W_8^1H[1] = x[5]$

$G[2]-W_8^2H[2] = x[6]$

$G[1]-W_8^3H[3] = x[7]$

以上是一個週期性序列。該系統的缺點是 K 不能分解到 4 點以下。現在讓我們將以上內容進一步分解。我們會得到類似這樣的結構

示例

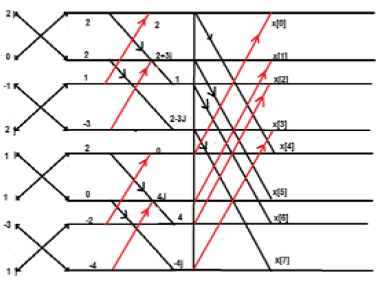
考慮序列 x[n]={ 2,1,-1,-3,0,1,2,1}。計算 FFT。

解答 - 給定的序列為 x[n]={ 2,1,-1,-3,0,1,2,1}

按如下所示排列項；