
- 數字訊號處理教程
- 數字訊號處理 - 首頁
- 數字訊號處理 - 訊號定義
- 數字訊號處理 - 基本 CT 訊號
- 數字訊號處理 - 基本 DT 訊號
- 數字訊號處理 - CT 訊號分類
- 數字訊號處理 - DT 訊號分類
- 數字訊號處理 - 其他訊號
- 基本系統特性
- 數字訊號處理 - 靜態系統
- 數字訊號處理 - 動態系統
- 數字訊號處理 - 因果系統
- 數字訊號處理 - 非因果系統
- 數字訊號處理 - 反因果系統
- 數字訊號處理 - 線性系統
- 數字訊號處理 - 非線性系統
- 數字訊號處理 - 時不變系統
- 數字訊號處理 - 時變系統
- 數字訊號處理 - 穩定系統
- 數字訊號處理 - 不穩定系統
- 數字訊號處理 - 例題解析
- 數字訊號處理資源
- 數字訊號處理 - 快速指南
- 數字訊號處理 - 有用資源
- 數字訊號處理 - 討論
數字訊號處理 - CT 訊號分類
連續時間訊號可以根據不同的條件或對訊號執行的操作進行分類。
偶訊號和奇訊號
偶訊號
如果訊號滿足以下條件,則稱其為偶訊號:
$$x(-t) = x(t)$$這裡,訊號的時間反轉不會導致幅度發生任何變化。例如,考慮下面所示的三角波。
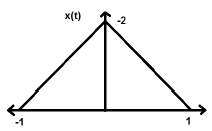
三角訊號是偶訊號,因為它關於 Y 軸對稱。我們可以說它是關於 Y 軸的映象。
考慮下圖所示的另一個訊號。
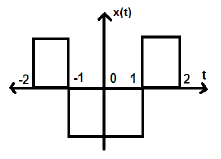
我們可以看到,上述訊號是偶訊號,因為它關於 Y 軸對稱。
奇訊號
如果訊號滿足以下條件,則稱其為奇訊號:
$$x(-t) = -x(t)$$這裡,時間反轉和幅度變化同時發生。
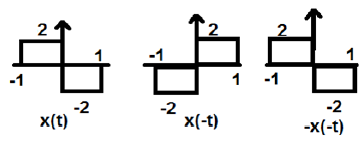
在上圖中,我們可以看到一個階躍訊號 x(t)。為了測試它是否是奇訊號,我們首先進行時間反轉,即 x(-t),結果如上圖所示。然後我們反轉所得訊號的幅度,即 –x(-t),結果如上圖所示。
如果我們比較第一個和第三個波形,我們可以看到它們是相同的,即 x(t)= -x(-t),這滿足我們的條件。因此,上述訊號是奇訊號。
一些與偶訊號和奇訊號相關的重要的結果如下所示。
- 偶 × 偶 = 偶
- 奇 × 奇 = 偶
- 偶 × 奇 = 奇
- 偶 ± 偶 = 偶
- 奇 ± 奇 = 奇
- 偶 ± 奇 = 既非偶也非奇
將任何訊號表示為偶數或奇數形式
有些訊號不能直接分類為偶數或奇數型別。它們表示為偶數和奇數訊號的組合。
$$x(t)\rightarrow x_{e}(t)+x_{0}(t)$$其中 xe(t) 表示偶訊號,xo(t) 表示奇訊號
$$x_{e}(t)=\frac{[x(t)+x(-t)]}{2}$$和
$$x_{0}(t)=\frac{[x(t)-x(-t)]}{2}$$示例
求訊號 $x(n) = t+t^{2}+t^{3}$ 的偶數和奇數部分
解 − 反轉 x(n),我們得到
$$x(-n) = -t+t^{2}-t^{3}$$
現在,根據公式,偶數部分
$$x_{e}(t) = \frac{x(t)+x(-t)}{2}$$
$$= \frac{[(t+t^{2}+t^{3})+(-t+t^{2}-t^{3})]}{2}$$
$$= t^{2}$$
類似地,根據公式,奇數部分是
$$x_{0}(t)=\frac{[x(t)-x(-t)]}{2}$$
$$= \frac{[(t+t^{2}+t^{3})-(-t+t^{2}-t^{3})]}{2}$$
$$= t+t^{3}$$
週期訊號和非週期訊號
週期訊號
週期訊號在一定時間間隔後重復自身。我們可以用等式形式表示為:
$$x(t) = x(t)\pm nT$$其中,n = 整數 (1,2,3……)
T = 基波週期 (FTP) ≠ 0 且 ≠∞
基波週期 (FTP) 是訊號具有周期性的最小正定值。
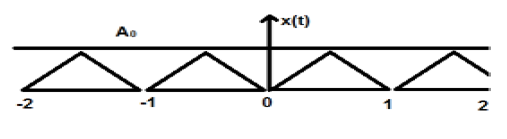
上圖顯示了一個幅度為 A 的三角訊號。這裡,訊號每 1 秒重複一次。因此,我們可以說該訊號是週期性的,其 FTP 為 1 秒。
非週期訊號
簡單地說,我們可以說,不是週期性的訊號本質上是非週期性的。顯然,這些訊號不會在任何時間間隔後重復自身。
非週期訊號不遵循一定的格式;因此,沒有特定的數學方程可以描述它們。
能量訊號和功率訊號
當且僅當包含的總能量有限且非零 (0<E<∞) 時,訊號被稱為能量訊號。因此,對於任何能量型訊號,總歸一化訊號都是有限且非零的。
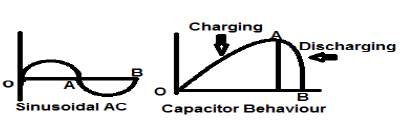
正弦交流電流訊號是能量型訊號的完美示例,因為它在一種情況下處於正半週期,而在下一半週期則為負。因此,其平均功率變為零。
無損電容器也是能量型訊號的完美示例,因為它在連線到電源時會充電到最佳水平,並且當電源移除時,它會透過負載耗散等量的能量,使其平均功率為零。
對於任何有限訊號 x(t),能量可以表示為 E,並寫成:
$$E = \int_{-\infty}^{+\infty} x^{2}(t)dt$$能量型訊號的頻譜密度給出了分佈在各個頻率水平上的能量量。
功率型訊號
當且僅當歸一化平均功率有限且非零,即 (0<p<∞) 時,訊號被稱為功率型訊號。對於功率型訊號,歸一化平均功率是有限且非零的。幾乎所有周期訊號都是功率訊號,它們的平均功率是有限且非零的。
用數學形式表示,訊號 x(t) 的功率可以寫成:
$$P = \lim_{T \rightarrow \infty}1/T\int_{-T/2}^{+T/2} x^{2}(t)dt$$能量訊號和功率訊號的區別
下表總結了能量訊號和功率訊號的區別。
| 功率訊號 | 能量訊號 |
|---|---|
| 實際的週期訊號是功率訊號。 | 非週期訊號是能量訊號。 |
| 這裡,歸一化平均功率有限且非零。 | 這裡,總歸一化能量有限且非零。 |
|
數學上, $$P = \lim_{T \rightarrow \infty}1/T\int_{-T/2}^{+T/2} x^{2}(t)dt$$ |
數學上, $$E = \int_{-\infty}^{+\infty} x^{2}(t)dt$$ |
| 這些訊號的存在時間是無限的。 | 這些訊號存在於有限的時間段內。 |
| 功率訊號的能量在無限時間內是無限的。 | 能量訊號的功率在無限時間內為零。 |
例題解析
例 1 − 求訊號 $z(t) = 2\cos(3\Pi t+30^{o})+4\sin(3\Pi +30^{o})$ 的功率
解 − 上述兩個訊號彼此正交,因為它們的頻率項彼此相同,並且它們具有相同的相位差。因此,總功率將是各個功率的總和。
設 $z(t) = x(t)+y(t)$
其中 $x(t) = 2\cos (3\Pi t+30^{o})$ 和 $y(t) = 4\sin(3\Pi +30^{o})$
x(t) 的功率 = $\frac{2^{2}}{2} = 2$
y(t) 的功率 = $\frac{4^{2}}{2} = 8$
因此,$P(z) = p(x)+p(y) = 2+8 = 10$…答案。
例 2 − 測試給定訊號 $x(t) = t^{2}+j\sin t$ 是否為共軛訊號?
解 − 這裡,實部 t2 為偶數,虛部 (虛部) $\sin t$ 為奇數。所以上述訊號是共軛訊號。
例 3 − 驗證 $X(t)= \sin \omega t$ 是否為奇訊號或偶訊號。
解 − 給定 $X(t) = \sin \omega t$
透過時間反轉,我們將得到 $\sin (-\omega t)$
但我們知道 $\sin(-\phi) = -\sin \phi$。
因此,
$$ \sin (-\omega t) = -\sin \omega t $$這滿足訊號為奇訊號的條件。因此,$\sin \omega t$ 是奇訊號。