DSA - 模式搜尋

什麼是模式搜尋？

模式搜尋/匹配演算法是一種用於在給定文字中定位或查詢特定模式或子字串的技術。其基本思想是在指定的資料結構中查詢特定模式的所有出現情況。例如，給定一個數字陣列[1, 2, 3, 4, 5, 6, 3, 4, 9]，我們需要在陣列中查詢模式[3, 4]的所有出現情況。答案將是索引號2和6。

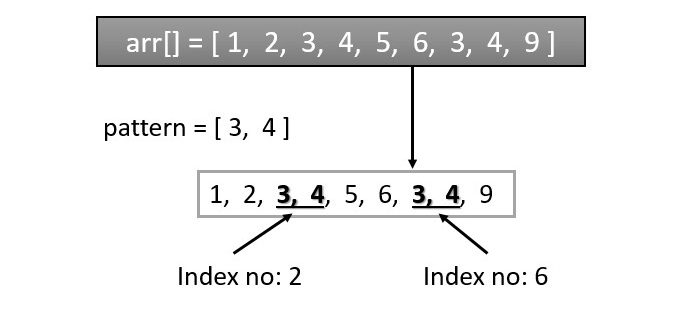
模式搜尋演算法如何工作？

有多種模式搜尋演算法以不同的方式工作。設計這些型別演算法的主要目標是降低時間複雜度。對於較長的文字，傳統方法可能需要大量時間才能完成模式搜尋任務。

如果我們說傳統方法，我們實際上是指蠻力法來解決模式搜尋問題。讓我們看看它是如何工作的 -

將模式滑過文字。
逐個比較每個字元。
如果所有字元都匹配，則表示找到匹配項。
如果不是，則將模式向右移動一個位置，並重復此過程，直到到達文字末尾或找到匹配項。

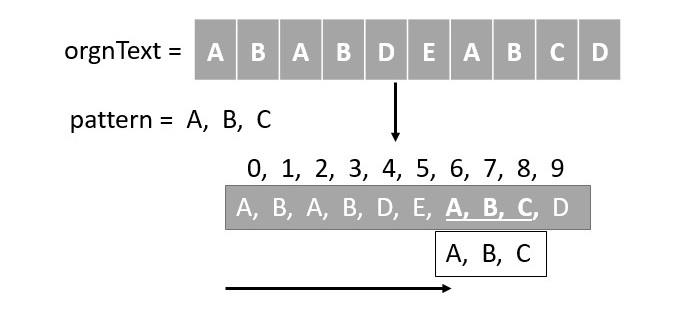
請記住，蠻力法是解決字串匹配或搜尋的最簡單方法，但它也是最慢、效率最低的方法。該演算法的時間複雜度為O(nm)，其中'n'是文字的長度，'m'是模式的長度。這意味著在最壞情況下，我們必須將文字的每個字元與模式的每個字元進行比較，如果n和m很大，這可能會非常慢。下一節中還提到了其他演算法。

示例

在本例中，我們將實際演示蠻力法在各種程式語言中解決模式匹配問題。

C C++ Java Python

#include <stdio.h>
#include <string.h>
// method to find match
void findMatch(char *orgText, char *pattern) {
   int n = strlen(orgText);
   int m = strlen(pattern);
   // comparing the text and pattern one by one
   for (int i = 0; i <= n-m; i++) {
      int j = 0;
      while (j < m && orgText[i+j] == pattern[j]) {
         j++;
      }
      // print result if found
      if (j == m) {
         printf("Oohhoo! Match found at index: %d\n", i);
         return; 
      }
   }
   // if not found
   printf("Oopps! No match found\n");
}
int main() {
   // Original Text
   char orgText[] = "Tutorials Point";
   // pattern to be matched
   char pattern[] = "Point";
   // method calling
   findMatch(orgText, pattern); 
   return 0;
}

#include <iostream>
#include <string>
using namespace std;
// method to find match
void findMatch(string orgText, string pattern) {
   int n = orgText.length();
   int m = pattern.length();
   // comparing the text and pattern one by one
   for (int i = 0; i <= n-m; i++) {
      int j = 0;
      while (j < m && orgText[i+j] == pattern[j]) {
         j++;
      }
      // print result if found
      if (j == m) {
         cout << "Oohhoo! Match found at index: " << i << endl;
         return; 
      }
   }
   // if not found
   cout << "Oopps! No match found" << endl;
}
int main() {
   // Original Text
   string orgText = "Tutorials Point";
   // pattern to be matched
   string pattern = "Point";
   // method calling
   findMatch(orgText, pattern); 
   return 0;
}

public class PattrnMatch {
   public static void main(String[] args) {
      // Original Text
      String orgText = "Tutorials Point";
      // pattern to be matched
      String pattern = "Point";
      // method calling
      findMatch(orgText, pattern); 
   }
   // method to find match
   public static void findMatch(String orgText, String pattern) {
      int n = orgText.length();
      int m = pattern.length();
      // comparing the text and pattern one by one
      for (int i = 0; i <= n-m; i++) {
         int j = 0;
         while (j < m && orgText.charAt(i+j) == pattern.charAt(j)) {
            j++;
         }
         // print result if found
         if (j == m) {
            System.out.println("Oohhoo! Match found at index: " + i);
               return; 
            }
      }
	  // if not found
	  System.out.println("Oopps! No match found");
   }
}

# method to find match
def findMatch(orgText, pattern):
   n = len(orgText)
   m = len(pattern)
   # comparing the text and pattern one by one
   for i in range(n-m+1):
      j = 0
      while j < m and orgText[i+j] == pattern[j]:
         j += 1
      # print result if found
      if j == m:
         print("Oohhoo! Match found at index:", i)
         return 
   # if not found
   print("Oopps! No match found")
# Original Text
orgText = "Tutorials Point"
# pattern to be matched
pattern = "Point"
# method calling
findMatch(orgText, pattern)

輸出

Oohhoo! Match found at index: 10

資料結構中的模式搜尋演算法

可以在資料結構上應用各種模式搜尋技術來檢索某些模式。只有當模式搜尋操作返回所需元素或其索引時，才認為該操作成功，否則，該操作被視為不成功。

以下是我們將在本教程中介紹的模式搜尋演算法列表 -

模式搜尋演算法的應用

模式搜尋演算法的應用如下 -

生物資訊學 - 它是一個將模式搜尋演算法應用於分析生物資料（例如DNA和蛋白質結構）的領域。
文字處理 - 文字處理涉及從文件集中查詢字串的任務。對於剽竊檢測、拼寫和語法檢查、搜尋引擎查詢等至關重要。
資料安全 - 模式匹配演算法可用於資料安全，透過建立惡意軟體檢測和密碼識別系統。
情感分析 - 透過匹配或檢測單詞的語氣，我們可以分析使用者的口音、情緒和情感。
推薦系統 - 我們還可以透過模式匹配演算法分析影片、音訊或任何部落格的內容，這將進一步有助於推薦其他內容。

列印頁面