樹遍歷

Table of content
上一頁
下一頁

遍歷是訪問樹中所有節點的過程，也可能列印它們的的值。因為所有節點都透過邊（連結）連線，我們總是從根（頭部）節點開始。也就是說，我們無法隨機訪問樹中的節點。有三種方法用於遍歷樹：

  • 中序遍歷

  • 先序遍歷

  • 後序遍歷

通常，我們遍歷樹是為了搜尋或定位樹中給定的項或鍵，或者列印它包含的所有值。

中序遍歷

在這種遍歷方法中，先訪問左子樹，然後訪問根節點，最後訪問右子樹。我們應該始終記住，每個節點本身都可以表示一個子樹。

如果二叉樹以**中序**方式遍歷，則輸出將以升序產生排序的鍵值。

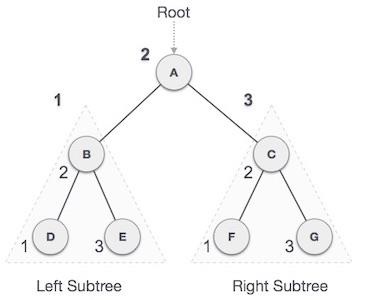
In-order Traversal

我們從**A**開始，按照中序遍歷，移動到它的左子樹**B**。**B**也以中序方式遍歷。這個過程一直持續到所有節點都被訪問。此樹的中序遍歷輸出將為：

D → B → E → A → F → C → G

演算法

直到所有節點都被遍歷：

Step 1 − Recursively traverse left subtree.
Step 2 − Visit root node.
Step 3 − Recursively traverse right subtree.

示例

以下是此操作在各種程式語言中的實現：

C C++ Java Python
#include <stdio.h>
#include <stdlib.h>
struct node {
   int data;
   struct node *leftChild;
   struct node *rightChild;
};
struct node *root = NULL;
void insert(int data){
   struct node *tempNode = (struct node*) malloc(sizeof(struct node));
   struct node *current;
   struct node *parent;
   tempNode->data = data;
   tempNode->leftChild = NULL;
   tempNode->rightChild = NULL;

   //if tree is empty
   if(root == NULL) {
      root = tempNode;
   } else {
      current = root;
      parent = NULL;
      while(1) {
         parent = current;

         //go to left of the tree
         if(data < parent->data) {
            current = current->leftChild;

            //insert to the left
            if(current == NULL) {
               parent->leftChild = tempNode;
               return;
            }
         }//go to right of the tree
         else {
            current = current->rightChild;

            //insert to the right
            if(current == NULL) {
               parent->rightChild = tempNode;
               return;
            }
         }
      }
   }
}
void inorder_traversal(struct node* root){
   if(root != NULL) {
      inorder_traversal(root->leftChild);
      printf("%d ",root->data);
      inorder_traversal(root->rightChild);
   }
}
int main(){
   int i;
   int array[7] = { 27, 14, 35, 10, 19, 31, 42 };
   for(i = 0; i < 7; i++)
      insert(array[i]);
   printf("Inorder traversal: ");
   inorder_traversal(root);
   return 0;
}

輸出

Inorder traversal: 10 14 19 27 31 35 42

#include <iostream>
struct node {
   int data;
   struct node *leftChild;
   struct node *rightChild;
};
struct node *root = NULL;
void insert(int data){
   struct node *tempNode = (struct node*) malloc(sizeof(struct node));
   struct node *current;
   struct node *parent;
   tempNode->data = data;
   tempNode->leftChild = NULL;
   tempNode->rightChild = NULL;

   //if tree is empty
   if(root == NULL) {
      root = tempNode;
   } else {
      current = root;
      parent = NULL;
      while(1) {
         parent = current;

         //go to left of the tree
         if(data < parent->data) {
            current = current->leftChild;

            //insert to the left
            if(current == NULL) {
               parent->leftChild = tempNode;
               return;
            }
         }//go to right of the tree
         else {
            current = current->rightChild;

            //insert to the right
            if(current == NULL) {
               parent->rightChild = tempNode;
               return;
            }
         }
      }
   }
}
void inorder_traversal(struct node* root){
   if(root != NULL) {
      inorder_traversal(root->leftChild);
      printf("%d ",root->data);
      inorder_traversal(root->rightChild);
   }
}
int main(){
   int i;
   int array[7] = { 27, 14, 35, 10, 19, 31, 42 };
   for(i = 0; i < 7; i++)
      insert(array[i]);
   printf("Inorder traversal: ");
   inorder_traversal(root);
   return 0;
}

輸出

Inorder traversal: 10 14 19 27 31 35 42 

class Node {
   int data;
   Node leftChild;
   Node rightChild;
   public Node(int key) {
      data = key;
      leftChild = rightChild = null;
   }
}
public class TreeDataStructure {
   Node root = null;
   void inorder_traversal(Node node) {
      if(node != null) {
         inorder_traversal(node.leftChild);
         System.out.print(node.data + " ");
         inorder_traversal(node.rightChild);
      }
   }
   public static void main(String args[]) {
      TreeDataStructure tree = new TreeDataStructure();
      tree.root = new Node(27);
      tree.root.leftChild = new Node(12);
      tree.root.rightChild = new Node(3);
      tree.root.leftChild.leftChild = new Node(44);
      tree.root.leftChild.rightChild = new Node(17);
      tree.root.rightChild.leftChild = new Node(56);
      System.out.println("Inorder traversal: ");
      tree.inorder_traversal(tree.root);
   }
}

輸出

Inorder traversal: 
44 12 17 27 56 3 

class Node:
   def __init__(self, key):
      self.leftChild = None
      self.rightChild = None
      self.data = key

# Create a function to perform inorder tree traversal
def InorderTraversal(root):
   if root:
      InorderTraversal(root.leftChild)
      print(root.data)
      InorderTraversal(root.rightChild)

# Main class
if __name__ == "__main__":
   root = Node(3)
   root.leftChild = Node(26)
   root.rightChild = Node(42)
   root.leftChild.leftChild = Node(54)
   root.leftChild.rightChild = Node(65)
   root.rightChild.leftChild = Node(12)

   # Function call
   print("Inorder traversal of binary tree is")
   InorderTraversal(root)

輸出

Inorder traversal of binary tree is
54
26
65
3
12
42

先序遍歷

在這種遍歷方法中，先訪問根節點，然後訪問左子樹，最後訪問右子樹。

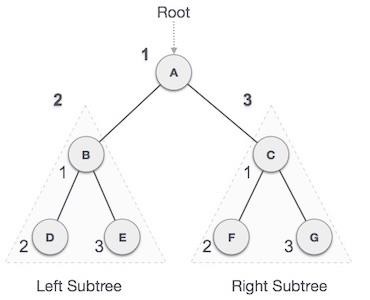
Pre-order Traversal

我們從**A**開始，按照先序遍歷，首先訪問**A**本身，然後移動到它的左子樹**B**。**B**也以先序方式遍歷。這個過程一直持續到所有節點都被訪問。此樹的先序遍歷輸出將為：

A → B → D → E → C → F → G

演算法

直到所有節點都被遍歷：

Step 1 − Visit root node.
Step 2 − Recursively traverse left subtree.
Step 3 − Recursively traverse right subtree.

示例

以下是此操作在各種程式語言中的實現：

C C++ Java Python
#include <stdio.h>
#include <stdlib.h>
struct node {
   int data;
   struct node *leftChild;
   struct node *rightChild;
};
struct node *root = NULL;
void insert(int data){
   struct node *tempNode = (struct node*) malloc(sizeof(struct node));
   struct node *current;
   struct node *parent;
   tempNode->data = data;
   tempNode->leftChild = NULL;
   tempNode->rightChild = NULL;

   //if tree is empty
   if(root == NULL) {
      root = tempNode;
   } else {
      current = root;
      parent = NULL;
      while(1) {
         parent = current;

         //go to left of the tree
         if(data < parent->data) {
            current = current->leftChild;

            //insert to the left
            if(current == NULL) {
               parent->leftChild = tempNode;
               return;
            }
         }//go to right of the tree
         else {
            current = current->rightChild;

            //insert to the right
            if(current == NULL) {
               parent->rightChild = tempNode;
               return;
            }
         }
      }
   }
}
void pre_order_traversal(struct node* root){
   if(root != NULL) {
      printf("%d ",root->data);
      pre_order_traversal(root->leftChild);
      pre_order_traversal(root->rightChild);
   }
}
int main(){
   int i;
   int array[7] = { 27, 14, 35, 10, 19, 31, 42 };
   for(i = 0; i < 7; i++)
      insert(array[i]);
   printf("Preorder traversal: ");
   pre_order_traversal(root);
   return 0;
}

輸出

Preorder traversal: 27 14 10 19 35 31 42 

#include <iostream>
struct node {
   int data;
   struct node *leftChild;
   struct node *rightChild;
};
struct node *root = NULL;
void insert(int data){
   struct node *tempNode = (struct node*) malloc(sizeof(struct node));
   struct node *current;
   struct node *parent;
   tempNode->data = data;
   tempNode->leftChild = NULL;
   tempNode->rightChild = NULL;

   //if tree is empty
   if(root == NULL) {
      root = tempNode;
   } else {
      current = root;
      parent = NULL;
      while(1) {
         parent = current;

         //go to left of the tree
         if(data < parent->data) {
            current = current->leftChild;

            //insert to the left
            if(current == NULL) {
               parent->leftChild = tempNode;
               return;
            }
         }//go to right of the tree
         else {
            current = current->rightChild;

            //insert to the right
            if(current == NULL) {
               parent->rightChild = tempNode;
               return;
            }
         }
      }
   }
}
void pre_order_traversal(struct node* root){
   if(root != NULL) {
      printf("%d ",root->data);
      pre_order_traversal(root->leftChild);
      pre_order_traversal(root->rightChild);
   }
}
int main(){
   int i;
   int array[7] = { 27, 14, 35, 10, 19, 31, 42 };
   for(i = 0; i < 7; i++)
      insert(array[i]);
   printf("Preorder traversal: ");
   pre_order_traversal(root);
   return 0;
}

輸出

Preorder traversal: 27 14 10 19 35 31 42 

class Node {
   int data;
   Node leftChild;
   Node rightChild;
   public Node(int key) {
      data = key;
      leftChild = rightChild = null;
   }
}
public class TreeDataStructure {
   Node root = null;
   void pre_order_traversal(Node node) {
      if(node != null) {
         System.out.print(node.data + " ");
         pre_order_traversal(node.leftChild);
         pre_order_traversal(node.rightChild);
      }
   }
   public static void main(String args[]) {
      TreeDataStructure tree = new TreeDataStructure();
      tree.root = new Node(27);
      tree.root.leftChild = new Node(12);
      tree.root.rightChild = new Node(3);
      tree.root.leftChild.leftChild = new Node(44);
      tree.root.leftChild.rightChild = new Node(17);
      tree.root.rightChild.leftChild = new Node(56);
      System.out.println("Preorder traversal: ");
      tree.pre_order_traversal(tree.root);
   }
}

輸出

Preorder traversal: 
27 12 44 17 3 56 

class Node:
   def __init__(self, key):
      self.leftChild = None
      self.rightChild = None
      self.data = key

# Create a function to perform postorder tree traversal
def PreorderTraversal(root):
   if root:
      print(root.data)
      PreorderTraversal(root.leftChild)
      PreorderTraversal(root.rightChild)

# Main class
if __name__ == "__main__":
   root = Node(3)
   root.leftChild = Node(26)
   root.rightChild = Node(42)
   root.leftChild.leftChild = Node(54)
   root.leftChild.rightChild = Node(65)
   root.rightChild.leftChild = Node(12)
   print("Preorder traversal of binary tree is")
   PreorderTraversal(root)

輸出

Preorder traversal of binary tree is
3
26
54
65
42
12

後序遍歷

在這種遍歷方法中，根節點最後被訪問，因此得名。首先遍歷左子樹，然後遍歷右子樹，最後遍歷根節點。

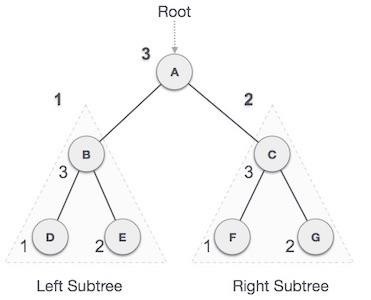
Post-order Traversal

我們從**A**開始，按照先序遍歷，首先訪問左子樹**B**。**B**也以後序方式遍歷。這個過程一直持續到所有節點都被訪問。此樹的後序遍歷輸出將為：

D → E → B → F → G → C → A

演算法

直到所有節點都被遍歷：

Step 1 − Recursively traverse left subtree.
Step 2 − Recursively traverse right subtree.
Step 3 − Visit root node.

示例

以下是此操作在各種程式語言中的實現：

C C++ Java Python
#include <stdio.h>
#include <stdlib.h>
struct node {
   int data;
   struct node *leftChild;
   struct node *rightChild;
};
struct node *root = NULL;
void insert(int data){
   struct node *tempNode = (struct node*) malloc(sizeof(struct node));
   struct node *current;
   struct node *parent;
   tempNode->data = data;
   tempNode->leftChild = NULL;
   tempNode->rightChild = NULL;

   //if tree is empty
   if(root == NULL) {
      root = tempNode;
   } else {
      current = root;
      parent = NULL;
      while(1) {
         parent = current;

         //go to left of the tree
         if(data < parent->data) {
            current = current->leftChild;

            //insert to the left
            if(current == NULL) {
               parent->leftChild = tempNode;
               return;
            }
         }//go to right of the tree
         else {
            current = current->rightChild;

            //insert to the right
            if(current == NULL) {
               parent->rightChild = tempNode;
               return;
            }
         }
      }
   }
}
void post_order_traversal(struct node* root){
   if(root != NULL) {
      post_order_traversal(root->leftChild);
      post_order_traversal(root->rightChild);
      printf("%d ", root->data);
   }
}
int main(){
   int i;
   int array[7] = { 27, 14, 35, 10, 19, 31, 42 };
   for(i = 0; i < 7; i++)
      insert(array[i]);
   printf("Post order traversal: ");
   post_order_traversal(root);
   return 0;
}

輸出

Post order traversal: 10 19 14 31 42 35 27

#include <iostream>
struct node {
   int data;
   struct node *leftChild;
   struct node *rightChild;
};
struct node *root = NULL;
void insert(int data){
   struct node *tempNode = (struct node*) malloc(sizeof(struct node));
   struct node *current;
   struct node *parent;
   tempNode->data = data;
   tempNode->leftChild = NULL;
   tempNode->rightChild = NULL;

   //if tree is empty
   if(root == NULL) {
      root = tempNode;
   } else {
      current = root;
      parent = NULL;
      while(1) {
         parent = current;

         //go to left of the tree
         if(data < parent->data) {
            current = current->leftChild;

            //insert to the left
            if(current == NULL) {
               parent->leftChild = tempNode;
               return;
            }
         }//go to right of the tree
         else {
            current = current->rightChild;

            //insert to the right
            if(current == NULL) {
               parent->rightChild = tempNode;
               return;
            }
         }
      }
   }
}
void post_order_traversal(struct node* root){
   if(root != NULL) {
      post_order_traversal(root->leftChild);
      post_order_traversal(root->rightChild);
      printf("%d ", root->data);
   }
}
int main(){
   int i;
   int array[7] = { 27, 14, 35, 10, 19, 31, 42 };
   for(i = 0; i < 7; i++)
      insert(array[i]);
   printf("Post order traversal: ");
   post_order_traversal(root);
   return 0;
}

輸出

Post order traversal: 10 19 14 31 42 35 27

class Node {
   int data;
   Node leftChild;
   Node rightChild;
   public Node(int key) {
      data = key;
      leftChild = rightChild = null;
   }
}
public class TreeDataStructure {
   Node root = null;
   void post_order_traversal(Node node) {
      if(node != null) {
         post_order_traversal(node.leftChild);
         post_order_traversal(node.rightChild);
         System.out.print(node.data + " ");
      }
   }
   public static void main(String args[]) {
      TreeDataStructure tree = new TreeDataStructure();
      tree.root = new Node(27);
      tree.root.leftChild = new Node(12);
      tree.root.rightChild = new Node(3);
      tree.root.leftChild.leftChild = new Node(44);
      tree.root.leftChild.rightChild = new Node(17);
      tree.root.rightChild.leftChild = new Node(56);
      System.out.println("Post order traversal: ");
      tree.post_order_traversal(tree.root);
   }
}

輸出

Post order traversal: 
44 17 12 56 3 27 

class Node:
   def __init__(self, key):
      self.leftChild = None
      self.rightChild = None
      self.data = key

# Create a function to perform preorder tree traversal
def PostorderTraversal(root):
   if root:
      PostorderTraversal(root.leftChild)
      PostorderTraversal(root.rightChild)
      print(root.data)

# Main class
if __name__ == "__main__":
   root = Node(3)
   root.leftChild = Node(26)
   root.rightChild = Node(42)
   root.leftChild.leftChild = Node(54)
   root.leftChild.rightChild = Node(65)
   root.rightChild.leftChild = Node(12)
   print("Postorder traversal of binary tree is")
   PostorderTraversal(root)

輸出

Postorder traversal of binary tree is
54
65
26
12
42
3

完整實現

現在讓我們看看樹遍歷在各種程式語言中的完整實現：

C C++ Java Python
#include <stdio.h>
#include <stdlib.h>
struct node {
   int data;
   struct node *leftChild;
   struct node *rightChild;
};
struct node *root = NULL;
void insert(int data){
   struct node *tempNode = (struct node*) malloc(sizeof(struct node));
   struct node *current;
   struct node *parent;
   tempNode->data = data;
   tempNode->leftChild = NULL;
   tempNode->rightChild = NULL;

//if tree is empty
   if(root == NULL) {
      root = tempNode;
   } else {
      current = root;
      parent = NULL;
      while(1) {
         parent = current;

         //go to left of the tree
         if(data < parent->data) {
            current = current->leftChild;

            //insert to the left
            if(current == NULL) {
               parent->leftChild = tempNode;
               return;
            }
         }//go to right of the tree
         else {
            current = current->rightChild;

            //insert to the right
            if(current == NULL) {
               parent->rightChild = tempNode;
               return;
            }
         }
      }
   }
}
void pre_order_traversal(struct node* root){
   if(root != NULL) {
      printf("%d ",root->data);
      pre_order_traversal(root->leftChild);
      pre_order_traversal(root->rightChild);
   }
}
void inorder_traversal(struct node* root){
   if(root != NULL) {
      inorder_traversal(root->leftChild);
      printf("%d ",root->data);
      inorder_traversal(root->rightChild);
   }
}
void post_order_traversal(struct node* root){
   if(root != NULL) {
      post_order_traversal(root->leftChild);
      post_order_traversal(root->rightChild);
      printf("%d ", root->data);
   }
}
int main(){
   int i;
   int array[7] = { 27, 14, 35, 10, 19, 31, 42 };
   for(i = 0; i < 7; i++)
      insert(array[i]);
   printf("Preorder traversal: ");
   pre_order_traversal(root);
   printf("\nInorder traversal: ");
   inorder_traversal(root);
   printf("\nPost order traversal: ");
   post_order_traversal(root);
   return 0;
}

輸出

Preorder traversal: 27 14 10 19 35 31 42 
Inorder traversal: 10 14 19 27 31 35 42 
Post order traversal: 10 19 14 31 42 35 27

#include <iostream>
struct node {
   int data;
   struct node *leftChild;
   struct node *rightChild;
};
struct node *root = NULL;
void insert(int data){
   struct node *tempNode = (struct node*) malloc(sizeof(struct node));
   struct node *current;
   struct node *parent;
   tempNode->data = data;
   tempNode->leftChild = NULL;
   tempNode->rightChild = NULL;

   //if tree is empty
   if(root == NULL) {
      root = tempNode;
   } else {
      current = root;
      parent = NULL;
      while(1) {
         parent = current;

         //go to left of the tree
         if(data < parent->data) {
            current = current->leftChild;

            //insert to the left
            if(current == NULL) {
               parent->leftChild = tempNode;
               return;
            }
         }//go to right of the tree
         else {
            current = current->rightChild;

            //insert to the right
            if(current == NULL) {
               parent->rightChild = tempNode;
               return;
            }
         }
      }
   }
}
void pre_order_traversal(struct node* root){
   if(root != NULL) {
      printf("%d ",root->data);
      pre_order_traversal(root->leftChild);
      pre_order_traversal(root->rightChild);
   }
}
void inorder_traversal(struct node* root){
   if(root != NULL) {
      inorder_traversal(root->leftChild);
      printf("%d ",root->data);
      inorder_traversal(root->rightChild);
   }
}
void post_order_traversal(struct node* root){
   if(root != NULL) {
      post_order_traversal(root->leftChild);
      post_order_traversal(root->rightChild);
      printf("%d ", root->data);
   }
}
int main(){
   int i;
   int array[7] = { 27, 14, 35, 10, 19, 31, 42 };
   for(i = 0; i < 7; i++)
      insert(array[i]);
   printf("Preorder traversal: ");
   pre_order_traversal(root);
   printf("\nInorder traversal: ");
   inorder_traversal(root);
   printf("\nPost order traversal: ");
   post_order_traversal(root);
   return 0;
}

輸出

Preorder traversal: 27 14 10 19 35 31 42 
Inorder traversal: 10 14 19 27 31 35 42 
Post order traversal: 10 19 14 31 42 35 27 

class Node {
   int data;
   Node leftChild;
   Node rightChild;
   public Node(int key) {
      data = key;
      leftChild = rightChild = null;
   }
}
public class TreeDataStructure {
   Node root = null;
   void inorder_traversal(Node node) {
      if(node != null) {
         inorder_traversal(node.leftChild);
         System.out.print(node.data + " ");
         inorder_traversal(node.rightChild);
      }
   }
   void pre_order_traversal(Node node) {
      if(node != null) {
         System.out.print(node.data + " ");
         pre_order_traversal(node.leftChild);
         pre_order_traversal(node.rightChild);
      }
   }
   void post_order_traversal(Node node) {
      if(node != null) {
         post_order_traversal(node.leftChild);
         post_order_traversal(node.rightChild);
         System.out.print(node.data + " ");
      }
   }
   public static void main(String args[]) {
      TreeDataStructure tree = new TreeDataStructure();
      tree.root = new Node(27);
      tree.root.leftChild = new Node(12);
      tree.root.rightChild = new Node(3);
      tree.root.leftChild.leftChild = new Node(44);
      tree.root.leftChild.rightChild = new Node(17);
      tree.root.rightChild.leftChild = new Node(56);
      System.out.println("Inorder traversal: ");
      tree.inorder_traversal(tree.root);
      System.out.println("\nPreorder traversal: ");
      tree.pre_order_traversal(tree.root);
      System.out.println("\nPost order traversal: ");
      tree.post_order_traversal(tree.root);
   }
}

輸出

Inorder traversal: 
44 12 17 27 56 3 
Preorder traversal: 
27 12 44 17 3 56 
Post order traversal: 
44 17 12 56 3 27 

class Node:
   def __init__(self, key):
      self.leftChild = None
      self.rightChild = None
      self.data = key

# Create a function to perform inorder tree traversal
def InorderTraversal(root):
   if root:
      InorderTraversal(root.leftChild)
      print(root.data)
      InorderTraversal(root.rightChild)

# Create a function to perform preorder tree traversal
def PostorderTraversal(root):
   if root:
      PostorderTraversal(root.leftChild)
      PostorderTraversal(root.rightChild)
      print(root.data)

# Create a function to perform postorder tree traversal
def PreorderTraversal(root):
   if root:
      print(root.data)
      PreorderTraversal(root.leftChild)
      PreorderTraversal(root.rightChild)

# Main class
if __name__ == "__main__":
   root = Node(3)
   root.leftChild = Node(26)
   root.rightChild = Node(42)
   root.leftChild.leftChild = Node(54)
   root.leftChild.rightChild = Node(65)
   root.rightChild.leftChild = Node(12)

   # Function call
   print("Inorder traversal of binary tree is")
   InorderTraversal(root)
   print("\nPreorder traversal of binary tree is")
   PreorderTraversal(root)
   print("\nPostorder traversal of binary tree is")
   PostorderTraversal(root)

輸出

Inorder traversal of binary tree is
54
26
65
3
12
42

Preorder traversal of binary tree is
3
26
54
65
42
12

Postorder traversal of binary tree is
54
65
26
12
42
3
列印頁面
上一頁
下一頁
廣告