Fisher-Yates 洗牌演算法

Fisher-Yates 洗牌演算法透過生成隨機排列來對有限序列的元素進行洗牌。每個排列出現的可能性是均等的。該演算法透過將序列的元素儲存在一個袋子中，並從袋子中隨機抽取每個元素來形成洗牌後的序列。

該演算法以 Ronald Fisher 和 Frank Yates 的名字命名，他們設計了最初的洗牌方法，該演算法是無偏的。它在相同條件下生成所有排列，因此獲得的輸出不受任何影響。然而，Fisher-Yates 演算法的現代版本比原始版本更有效率。

Fisher-Yates 演算法

原始方法

洗牌演算法的原始方法涉及使用筆和紙來生成有限序列的隨機排列。生成隨機排列的演算法如下：

步驟 1 - 寫下有限序列中的所有元素。宣告一個單獨的列表來儲存獲得的輸出。

步驟 2 - 在輸入序列中隨機選擇一個元素 i 並將其新增到輸出列表中。將元素 i 標記為已訪問。

步驟 3 - 重複步驟 2，直到有限序列中的所有元素都被訪問並隨機新增到輸出列表中。

步驟 4 - 程序終止後生成的輸出列表是生成的隨機排列。

現代演算法

現代演算法是對原始 Fisher-Yates 洗牌演算法的略微修改版本。修改的主要目標是透過降低原始方法的時間複雜度來使原始演算法計算機化。現代方法由 Richard Durstenfeld 開發，並由 Donald E. Knuth 推廣。

因此，現代方法使用交換而不是維護另一個輸出列表來儲存生成的隨機排列。時間複雜度從 O(n²) 降低到 O(n)。演算法如下：

步驟 1 - 將元素 1 到 n 寫入有限序列中。

步驟 2 - 在輸入序列中隨機選擇一個元素 i 並將其與列表中最後一個未訪問的元素交換。

步驟 3 - 重複步驟 2，直到有限序列中的所有元素都被訪問並交換。

步驟 4 - 程序終止後生成的列表是隨機排列序列。

虛擬碼

以下現代方法虛擬碼中，洗牌是從陣列的最高索引到最低索引進行的。

Fisher-Yates Shuffle (array of n elements):
for i from n−1 downto 1 do
   j ← random integer such that 0 ≤ j ≤ i
   exchange a[j] and a[i]

以下現代方法虛擬碼中，洗牌是從陣列的最低索引到最高索引進行的。

Fisher-Yates Shuffle (array of n elements):
for i from 0 to n−2 do
   j ← random integer such that i ≤ j < n
   exchange a[i] and a[j]

原始方法示例

為了更好地描述該演算法，讓我們對字母表的前六個字母給定的有限序列進行排列。輸入序列：A B C D E F。

步驟 1

這稱為筆和紙方法。我們考慮一個儲存有限序列的輸入陣列和一個儲存結果的輸出陣列。

步驟 2

隨機選擇任何元素並將其新增到輸出列表中，然後將其標記為已檢查。在本例中，我們選擇元素 C。

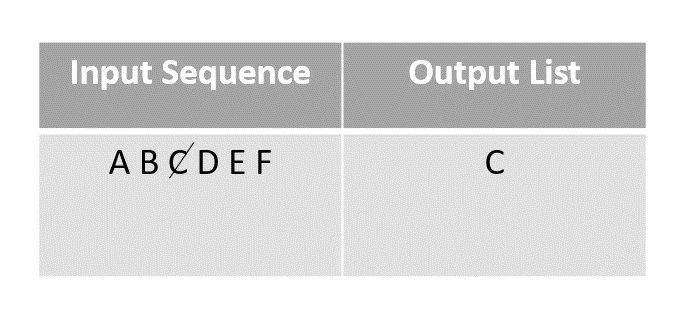
步驟 3

接下來隨機選擇的元素是 E，它被標記並新增到輸出列表中。

步驟 4

然後隨機函式選擇下一個元素 A 並將其新增到輸出陣列中，然後將其標記為已訪問。

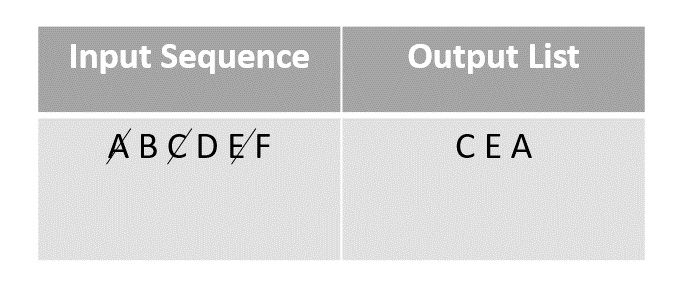
步驟 5

然後從輸入序列中剩餘的元素中選擇 F 並將其新增到輸出中，然後將其標記為已訪問。

步驟 6

下一個要新增到隨機排列中的元素是 D。它被標記並新增到輸出陣列中。

步驟 7

輸入列表中最後一個元素將是 B，因此它被標記並最終新增到輸出列表中。

現代方法示例

為了降低原始方法的時間複雜度，引入了現代演算法。現代方法使用交換來洗牌序列 - 例如，該演算法的工作原理類似於透過交換原始牌組中的位置來洗牌一副紙牌。讓我們來看一個例子，瞭解 Fisher-Yates 演算法的現代版本是如何工作的。

步驟 1

將字母表的前幾個字母作為輸入，並使用現代方法對其進行洗牌。

步驟 2

隨機選擇元素 D 並將其與序列中最後一個未標記的元素（在本例中為 F）交換。

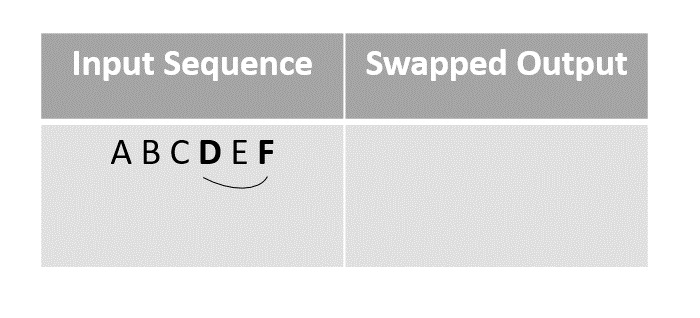
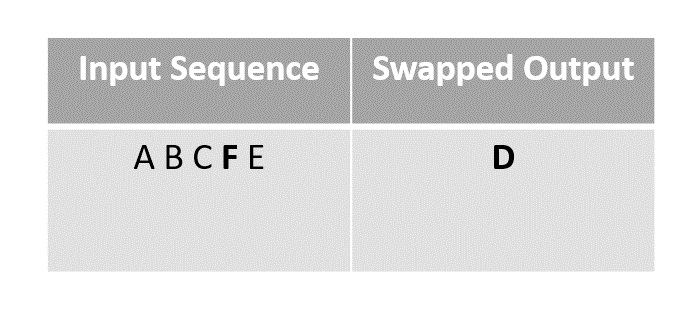
步驟 3

下一步，我們選擇元素 B 與最後一個未標記的元素“E”交換，因為在前面的步驟中，F 與 D 交換後被移動到 D 的位置。

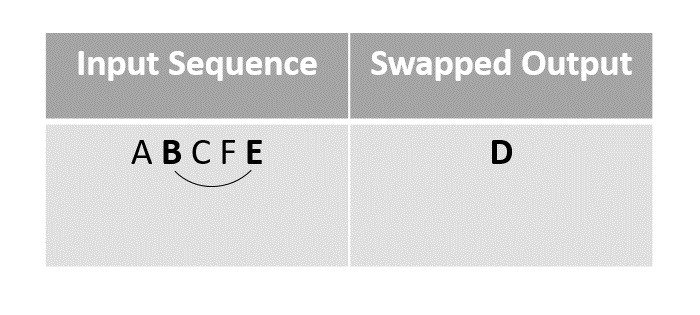
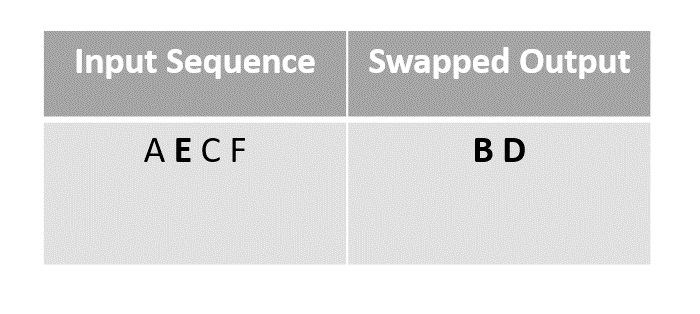
步驟 4

接下來，我們將元素 A 與 F 交換，因為它是在列表中最後一個未標記的元素。

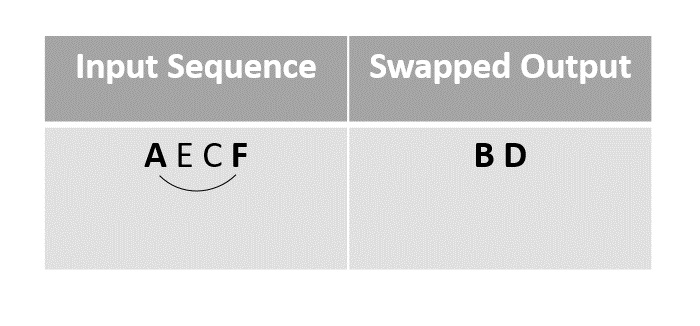
步驟 5

然後元素 F 與最後一個未標記的元素 C 交換。

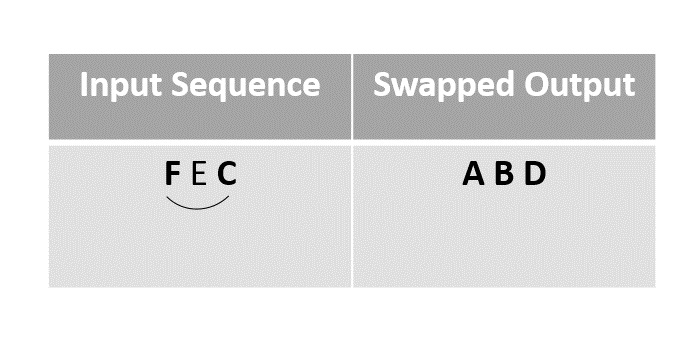
步驟 6

序列中剩餘的元素最終可以交換，但由於隨機函式選擇了 E 作為元素，因此它保持不變。

步驟 7

剩餘的元素 C 保持不變，無需交換。

交換後獲得的陣列是最終的輸出陣列。

示例

以下是上述方法在各種程式語言中的實現：

#include <stdio.h>
#include <stdlib.h>
#include <time.h>
// Function to perform Fisher-Yates Shuffle using the original method
void fisherYatesShuffle(char arr[], char n) {
    char output[n];  // Create an output array to store the shuffled elements
    char visited[n]; // Create a boolean array to keep track of visited elements
    // Initialize the visited array with zeros (false)
    for (char i = 0; i < n; i++) {
        visited[i] = 0;
    }
    // Perform the shuffle algorithm
    for (char i = 0; i < n; i++) {
        char j = rand() % n; // Generate a random index in the input array
        while (visited[j]) { // Find the next unvisited index
            j = rand() % n;
        }
        output[i] = arr[j]; // Add the element at the chosen index to the output array
        visited[j] = 1;     // Mark the element as visited
    }
    // Copy the shuffled elements back to the original array
    for (char i = 0; i < n; i++) {
        arr[i] = output[i];
    }
}
int main() {
    char arr[] = {'A', 'B', 'C', 'D', 'E', 'F'};
    char n = sizeof(arr) / sizeof(arr[0]);

    srand(time(NULL)); // Seed the random number generator with the current time
    fisherYatesShuffle(arr, n); // Call the shuffle function
    printf("Shuffled array: ");
    for (char i = 0; i < n; i++) {
        printf("%c ", arr[i]); // Print the shuffled array
    }
    printf("\n");
    return 0;
}

Shuffled array: A B F D E C 

#include <iostream>
#include <vector>
#include <algorithm>
#include <random>
// Function to perform Fisher-Yates Shuffle using the original method
void fisherYatesShuffle(std::vector<char>& arr) {
    std::vector<char> output; // Create an output vector to store the shuffled elements
    std::vector<bool> visited(arr.size(), false); // Create a boolean vector to keep track of visited elements
    // Perform the shuffle algorithm
    for (char i = 0; i < arr.size(); i++) {
        char j = rand() % arr.size(); // Generate a random index in the input vector
        while (visited[j]) { // Find the next unvisited index
            j = rand() % arr.size();
        }
        output.push_back(arr[j]); // Add the element at the chosen index to the output vector
        visited[j] = true; // Mark the element as visited
    }
    arr = output; // Copy the shuffled elements back to the original vector
}
int main() {
    std::vector<char> arr = {'A', 'B', 'C', 'D', 'E', 'F'};
    srand(time(NULL)); // Seed the random number generator with the current time
    fisherYatesShuffle(arr); // Call the shuffle function
    std::cout << "Shuffled array: ";
    for (char c : arr) {
        std::cout << c << " "; // Print the shuffled array
    }
    std::cout << std::endl;
    return 0;
}

Shuffled array: D B A F C E

import java.util.ArrayList;
import java.util.List;
import java.util.Random;
public class FisherYatesShuffle {
    // Function to perform Fisher-Yates Shuffle using the original method
    public static List<Character> fisherYatesShuffle(List<Character> arr) {
        List<Character> output = new ArrayList<>(); // Create an output list to store the shuffled elements
        boolean[] visited = new boolean[arr.size()]; // Create a boolean array to keep track of visited elements
        // Perform the shuffle algorithms
        for (int i = 0; i < arr.size(); i++) {
            int j = new Random().nextInt(arr.size()); // Generate a random index in the input list
            while (visited[j]) { // Find the next unvisited index
                j = new Random().nextInt(arr.size());
            }
            output.add(arr.get(j)); // Add the element at the chosen index to the output list
            visited[j] = true; // Mark the element as visited
        }
        return output;
    }
    public static void main(String[] args) {
        List<Character> arr = List.of('A', 'B', 'C', 'D', 'E', 'F');
        Random rand = new Random(); // Seed the random number generator with the current time
        List<Character> shuffledArray = fisherYatesShuffle(arr); // Call the shuffle function
        System.out.print("Shuffled array: ");
        for (char c : shuffledArray) {
            System.out.print(c + " "); // Print the shuffled array
        }
        System.out.println();
    }
}

Shuffled array: D B E C A F 

import random
# Function to perform Fisher-Yates Shuffle using the original method
def fisherYatesShuffle(arr):
    output = []  # Create an output list to store the shuffled elements
    visited = [False] * len(
        arr)  # Create a boolean list to keep track of visited elements
    # Perform the shuffle algorithm
    for i in range(len(arr)):
        j = random.randint(0,
                           len(arr) -
                           1)  # Generate a random index in the input list
        while visited[j]:  # Find the next unvisited index
            j = random.randint(0, len(arr) - 1)
        output.append(
            arr[j])  # Add the element at the chosen index to the output list
        visited[j] = True  # Mark the element as visited
    return output
if __name__ == "__main__":
    arr = ['A', 'B', 'C', 'D', 'E', 'F']
    random.seed()  # Seed the random number generator with the current time
    shuffled_array = fisherYatesShuffle(arr)  # Call the shuffle function
    print("Shuffled array:", shuffled_array)  # Print the shuffled array

Shuffled array: ['D', 'C', 'A', 'B', 'F', 'E']