深度優先搜尋 (DFS) 演算法

深度優先搜尋 (DFS) 演算法是一種用於搜尋圖或樹資料結構所有頂點的遞迴演算法。此演算法以深度優先的方式遍歷圖，並使用棧來記住在任何迭代中遇到死衚衕時要開始搜尋的下一個頂點。

如上例所示，DFS 演算法首先從 S 遍歷到 A、D、G、E、B，然後到 F，最後到 C。它採用以下規則。

規則 1 - 訪問相鄰的未訪問頂點。將其標記為已訪問。顯示它。將其壓入棧中。
規則 2 - 如果未找到相鄰頂點，則從棧中彈出頂點。（它將彈出棧中所有沒有相鄰頂點的頂點。）
規則 3 - 重複規則 1 和規則 2，直到棧為空。

步驟	遍歷	描述
1		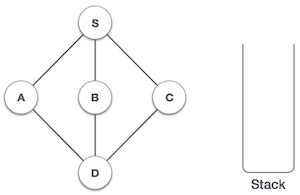初始化棧。
2		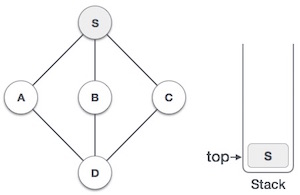將 S 標記為已訪問，並將其壓入棧中。探索 S 的任何未訪問的相鄰節點。我們有三個節點，我們可以選擇其中任何一個。在本例中，我們將按字母順序選擇節點。
3		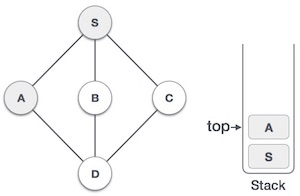將 A 標記為已訪問，並將其壓入棧中。探索 A 的任何未訪問的相鄰節點。S 和 D 都與 A 相鄰，但我們只關心未訪問的節點。
4		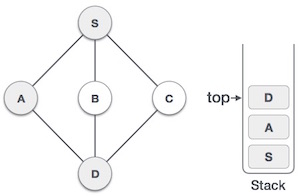訪問 D，將其標記為已訪問，並將其壓入棧中。這裡，我們有 B 和 C 節點，它們與 D 相鄰，並且都未訪問。但是，我們仍將按字母順序選擇。
5		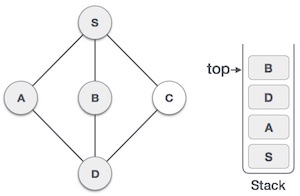我們選擇 B，將其標記為已訪問，並將其壓入棧中。這裡 B 沒有未訪問的相鄰節點。因此，我們從棧中彈出 B。
6		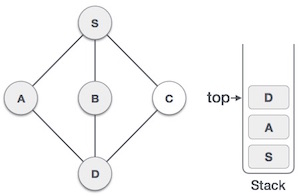我們檢查棧頂以返回到上一個節點，並檢查它是否有任何未訪問的節點。在這裡，我們發現 D 在棧頂。
7		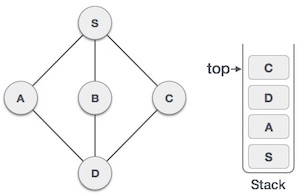現在，D 唯一未訪問的相鄰節點是 C。因此，我們訪問 C，將其標記為已訪問，並將其壓入棧中。

由於 C 沒有未訪問的相鄰節點，因此我們繼續彈出棧，直到找到一個具有未訪問相鄰節點的節點。在本例中，沒有這樣的節點，我們繼續彈出直到棧為空。

示例

以下是深度優先搜尋 (DFS) 演算法在各種程式語言中的實現 -

C C++ Java Python

#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#define MAX 5
struct Vertex {
   char label;
   bool visited;
};
//stack variables
int stack[MAX]; 
int top = -1; 
//graph variables
//array of vertices
struct Vertex* lstVertices[MAX];
//adjacency matrix
int adjMatrix[MAX][MAX];
//vertex count
int vertexCount = 0;
//stack functions
void push(int item) { 
   stack[++top] = item; 
} 
int pop() { 
   return stack[top--]; 
} 
int peek() {
   return stack[top];
}
bool isStackEmpty() {
   return top == -1;
}
//graph functions

//add vertex to the vertex list
void addVertex(char label) {
   struct Vertex* vertex = (struct Vertex*) malloc(sizeof(struct Vertex));
   vertex->label = label;  
   vertex->visited = false;     
   lstVertices[vertexCount++] = vertex;
}
//add edge to edge array
void addEdge(int start,int end) {
   adjMatrix[start][end] = 1;
   adjMatrix[end][start] = 1;
}
//display the vertex
void displayVertex(int vertexIndex) {
   printf("%c ",lstVertices[vertexIndex]->label);
}       
//get the adjacent unvisited vertex
int getAdjUnvisitedVertex(int vertexIndex) {
   int i;
   for(i = 0; i < vertexCount; i++) {
      if(adjMatrix[vertexIndex][i] == 1 && lstVertices[i]->visited == false) {
         return i;
      }
   }
   return -1;
}
void depthFirstSearch() {
   int i;
   //mark first node as visited
   lstVertices[0]->visited = true;
   //display the vertex
   displayVertex(0);   
   //push vertex index in stack
   push(0);
   while(!isStackEmpty()) {
      //get the unvisited vertex of vertex which is at top of the stack
      int unvisitedVertex = getAdjUnvisitedVertex(peek());
      //no adjacent vertex found
      if(unvisitedVertex == -1) {
         pop();
      } else {
         lstVertices[unvisitedVertex]->visited = true;
         displayVertex(unvisitedVertex);
         push(unvisitedVertex);
      }
   }
   //stack is empty, search is complete, reset the visited flag        
   for(i = 0;i < vertexCount;i++) {
      lstVertices[i]->visited = false;
   }        
}
int main() {
   int i, j;

   for(i = 0; i < MAX; i++) {   // set adjacency
      for(j = 0; j < MAX; j++) // matrix to 0
         adjMatrix[i][j] = 0;
   }
   addVertex('S');   // 0
   addVertex('A');   // 1
   addVertex('B');   // 2
   addVertex('C');   // 3
   addVertex('D');   // 4
   addEdge(0, 1);    // S - A
   addEdge(0, 2);    // S - B
   addEdge(0, 3);    // S - C
   addEdge(1, 4);    // A - D
   addEdge(2, 4);    // B - D
   addEdge(3, 4);    // C - D
   printf("Depth First Search: ");
   depthFirstSearch(); 
   return 0;   
}

輸出

Depth First Search: S A D B C

//C++ code for Depth First Traversal
#include <iostream>
#include <array>
#include <vector>
constexpr int MAX = 5;
struct Vertex {
   char label;
   bool visited;
};
//stack variables
std::array<int, MAX> stack;
int top = -1;
//graph variables
//array of vertices 
std::array<Vertex*, MAX> lstVertices;
//adjacency matrix
std::array<std::array<int, MAX>, MAX> adjMatrix;
//vertex count
int vertexCount = 0;
//stack functions
void push(int item) {
   stack[++top] = item;
}
int pop() {
   return stack[top--];
}
int peek() {
   return stack[top];
}
bool isStackEmpty() {
   return top == -1;
}
//graph functions
//add vertex to the vertex list
void addVertex(char label) {
   Vertex* vertex = new Vertex;
   vertex->label = label;
   vertex->visited = false;
   lstVertices[vertexCount++] = vertex;
}

//add edge to edge array
void addEdge(int start, int end) {
   adjMatrix[start][end] = 1;
   adjMatrix[end][start] = 1;
}

//display the vertex
void displayVertex(int vertexIndex) {
   std::cout << lstVertices[vertexIndex]->label << " ";
}
//get the adjacent unvisited vertex
int getAdjUnvisitedVertex(int vertexIndex) {
   for (int i = 0; i < vertexCount; i++) {
      if (adjMatrix[vertexIndex][i] == 1 && !lstVertices[i]->visited) {
         return i;
      }
   }
   return -1;
}
//mark first node as visited
void depthFirstSearch() {
   lstVertices[0]->visited = true;
   //display the vertex
   displayVertex(0);
   //push vertex index in stack
   push(0);
   while (!isStackEmpty()) {
       //get the unvisited vertex of vertex which is at top of the stack
      int unvisitedVertex = getAdjUnvisitedVertex(peek());
      //no adjacent vertex found
      if (unvisitedVertex == -1) {
         pop();
      } else {
         lstVertices[unvisitedVertex]->visited = true;
         displayVertex(unvisitedVertex);
         push(unvisitedVertex);
      }
   }
   //stack is empty, search is complete, reset the visited flag
   for (int i = 0; i < vertexCount; i++) {
      lstVertices[i]->visited = false;
   }
}
int main() {
   for (int i = 0; i < MAX; i++) {   //set adjacency
      for (int j = 0; j < MAX; j++) {    // matrix to 0
         adjMatrix[i][j] = 0;
      }
   }
   addVertex('S');
   addVertex('A');
   addVertex('B');
   addVertex('C');
   addVertex('D');
   addEdge(0, 1);
   addEdge(0, 2);
   addEdge(0, 3);
   addEdge(1, 4);
   addEdge(2, 4);
   addEdge(3, 4);
   std::cout << "Depth First Search: ";
   depthFirstSearch();
   return 0;
}

輸出

Depth First Search: S A D B C

//Java program for Depth First Traversal
public class DepthFirstSearch {
    private static final int MAX = 5;
    private static class Vertex {
        char label;
        boolean visited;
    }
    private static int[] stack = new int[MAX];
    private static int top = -1;
    private static Vertex[] lstVertices = new Vertex[MAX];
    private static int[][] adjMatrix = new int[MAX][MAX];
    private static int vertexCount = 0;
    private static void push(int item) {
        stack[++top] = item;
    }
    private static int pop() {
        return stack[top--];
    }
    private static int peek() {
        return stack[top];
    }
    private static boolean isStackEmpty() {
        return top == -1;
    }
    private static void addVertex(char label) {
        Vertex vertex = new Vertex();
        vertex.label = label;
        vertex.visited = false;
        lstVertices[vertexCount++] = vertex;
    }
    private static void addEdge(int start, int end) {
        adjMatrix[start][end] = 1;
        adjMatrix[end][start] = 1;
    }
    private static void displayVertex(int vertexIndex) {
        System.out.print(lstVertices[vertexIndex].label + " ");
    }
    private static int getAdjUnvisitedVertex(int vertexIndex) {
        for (int i = 0; i < vertexCount; i++) {
            if (adjMatrix[vertexIndex][i] == 1 && !lstVertices[i].visited) {
                return i;
            }
        }
        return -1;
    }
    private static void depthFirstSearch() {
        lstVertices[0].visited = true;
        displayVertex(0);
        push(0);
        while (!isStackEmpty()) {
            int unvisitedVertex = getAdjUnvisitedVertex(peek());

            if (unvisitedVertex == -1) {
                pop();
            } else {
                lstVertices[unvisitedVertex].visited = true;
                displayVertex(unvisitedVertex);
                push(unvisitedVertex);
            }
        }
        for (int i = 0; i < vertexCount; i++) {
            lstVertices[i].visited = false;
        }
    }
    public static void main(String[] args) {
        for (int i = 0; i < MAX; i++) {
            for (int j = 0; j < MAX; j++) {
                adjMatrix[i][j] = 0;
            }
        }
        addVertex('S');   // 0
        addVertex('A');   // 1
        addVertex('B');   // 2
        addVertex('C');   // 3
        addVertex('D');   // 4
        addEdge(0, 1);    // S - A
        addEdge(0, 2);    // S - B
        addEdge(0, 3);    // S - C
        addEdge(1, 4);    // A - D
        addEdge(2, 4);    // B - D
        addEdge(3, 4);    // C - D
        System.out.print("Depth First Search: ");
        depthFirstSearch();
    }
}

輸出

Depth First Search: S A D B C

#Python program for Depth First Traversal
MAX = 5
class Vertex:
    def __init__(self, label):
        self.label = label
        self.visited = False
#stack variables
stack = []
top = -1
#graph variables
#array of vertices
lstVertices = [None] * MAX
#adjacency matrix
adjMatrix = [[0] * MAX for _ in range(MAX)]
#vertex count
vertexCount = 0
#stack functions
def push(item):
    global top
    top += 1
    stack.append(item)
def pop():
    global top
    item = stack[top]
    del stack[top]
    top -= 1
    return item
def peek():
    return stack[top]
def isStackEmpty():
    return top == -1
#graph functions
#add vertex to the vertex list
def addVertex(label):
    global vertexCount
    vertex = Vertex(label)
    lstVertices[vertexCount] = vertex
    vertexCount += 1
#add edge to edge array
def addEdge(start, end):
    adjMatrix[start][end] = 1
    adjMatrix[end][start] = 1
#Display the Vertex
def displayVertex(vertexIndex):
    print(lstVertices[vertexIndex].label, end=' ')
def getAdjUnvisitedVertex(vertexIndex):
    for i in range(vertexCount):
        if adjMatrix[vertexIndex][i] == 1 and not lstVertices[i].visited:
            return i
    return -1
def depthFirstSearch():
    lstVertices[0].visited = True
    displayVertex(0)
    push(0)
    while not isStackEmpty():
        unvisitedVertex = getAdjUnvisitedVertex(peek())
        if unvisitedVertex == -1:
            pop()
        else:
            lstVertices[unvisitedVertex].visited = True
            displayVertex(unvisitedVertex)
            push(unvisitedVertex)
    for i in range(vertexCount):
        lstVertices[i].visited = False
for i in range(MAX):
    for j in range(MAX):
        adjMatrix[i][j] = 0
addVertex('S')   # 0
addVertex('A')   # 1
addVertex('B')   # 2
addVertex('C')   # 3
addVertex('D')   # 4
addEdge(0, 1)    # S - A
addEdge(0, 2)    # S - B
addEdge(0, 3)    # S - C
addEdge(1, 4)    # A - D
addEdge(2, 4)    # B - D
addEdge(3, 4)    # C - D
print("Depth First Search:", end=' ')
depthFirstSearch()

輸出

Depth First Search: S A D B C

點選檢視深度優先搜尋 (BFS) 演算法的 C 語言實現

DFS 演算法的複雜度

時間複雜度

DFS 演算法的時間複雜度表示為 O(V + E) 的形式，其中 V 是節點數，E 是邊數。

空間複雜度

DFS 演算法的空間複雜度為 O(V)。

列印頁面