樹形資料結構

---

---

樹形資料結構

樹是一種非線性的抽象資料型別，具有層次結構。它由節點（儲存資料的地方）透過連結連線而成。樹形資料結構源於單個稱為根節點的節點，並具有連線到根的子樹。

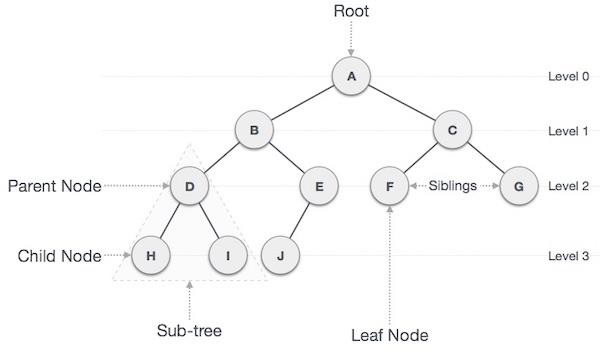
重要術語

以下是關於樹的重要術語。

• 路徑 − 路徑指的是沿著樹的邊的節點序列。

• 根 − 樹頂部的節點稱為根。每棵樹只有一個根，並且從根節點到任何節點只有一條路徑。

• 父節點 − 除根節點外的任何節點都有一條向上連線到稱為父節點的節點的邊。

• 子節點 − 下方由其向下邊連線的給定節點稱為其子節點。

• 葉子節點 − 沒有子節點的節點稱為葉子節點。

• 子樹 − 子樹表示節點的後代。

• 訪問 − 訪問是指當控制處於節點上時檢查節點的值。

• 遍歷 − 遍歷意味著以特定順序透過節點。

• 層級 − 節點的層級表示節點的代數。如果根節點在第0層，則其下一個子節點在第1層，其孫子節點在第2層，依此類推。

• 鍵 − 鍵表示節點的值，根據該值將對節點進行搜尋操作。

樹的型別

樹有三種類型：

• 一般樹

• 二叉樹

• 二叉搜尋樹

一般樹

一般樹是非有序的樹形資料結構，其中根節點最多有0個或n個子樹。

一般樹對它們的層次結構沒有約束。因此，根節點充當所有其他子樹的超集。

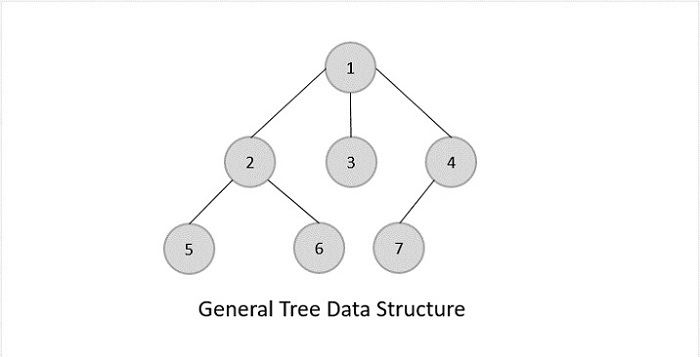
二叉樹

二叉樹是一般樹，其中根節點最多隻能包含2個子樹：左子樹和右子樹。根據子節點的數量，二叉樹分為三種類型。

滿二叉樹

• 滿二叉樹是一種二叉樹型別，其中每個節點都具有0個或2個子節點。

完全二叉樹

• 完全二叉樹是一種二叉樹型別，其中所有葉子節點都必須位於同一層。但是，完全二叉樹中的根節點和內部節點可以具有0、1或2個子節點。

完美二叉樹

• 完美二叉樹是一種二叉樹型別，其中所有葉子節點都位於同一層，並且除葉子節點外的每個節點都有2個子節點。

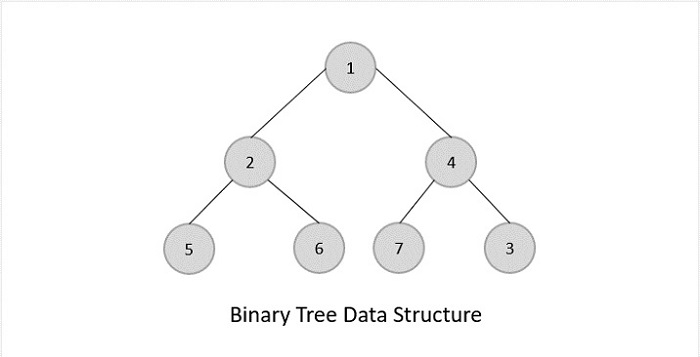
二叉搜尋樹

二叉搜尋樹具有二叉樹的所有屬性，包括一些基於某些約束的額外屬性，使其比二叉樹更有效。

二叉搜尋樹 (BST) 中的資料總是以這樣的方式儲存：左子樹中的值總是小於根節點中的值，而右子樹中的值總是大於根節點中的值，即左子樹 < 根節點 ≤ 右子樹。

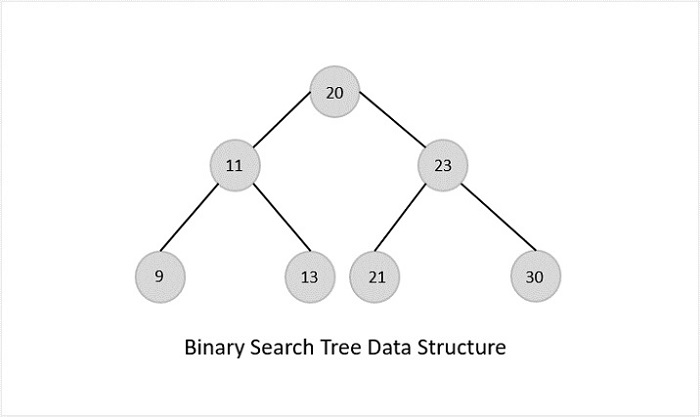
BST 的優點

• 二叉搜尋樹比二叉樹更有效，因為執行各種操作的時間複雜度降低了。

• 由於鍵的順序僅基於父節點，因此搜尋操作變得更簡單。

• BST 的排列也有利於範圍查詢，範圍查詢用於查詢兩個鍵之間存在的值。這有助於資料庫管理系統。

BST 的缺點

二叉搜尋樹的主要缺點是，如果節點中的所有元素都大於或小於根節點，樹將變得傾斜。簡單地說，樹完全傾斜到一邊。

這種傾斜將使樹成為連結串列而不是 BST，因為搜尋操作的最壞情況時間複雜度變為 O(n)。

為了克服二叉搜尋樹的傾斜問題，引入了平衡二叉搜尋樹的概念。

平衡二叉搜尋樹

考慮一個二叉搜尋樹，其中左子樹的高度為“m”，右子樹的高度為“n”。如果 (m-n) 的值為 0、1 或 -1，則該樹被稱為平衡二叉搜尋樹。

樹的設計方式是在高度差超過 1 時自動平衡。二叉搜尋樹使用旋轉作為自平衡演算法。有四種不同的旋轉型別：左左、右右、左右、右左。

有各種型別的自平衡二叉搜尋樹：

• AVL 樹

• 紅黑樹

• B 樹

• B+ 樹

• 伸展樹

• 優先搜尋樹