圖資料結構

上一頁
下一頁

什麼是圖？

圖是一種抽象資料型別 (ADT)，它由一組透過連結相互連線的物件組成。相互連線的物件由稱為頂點的點表示，連線頂點的連結稱為邊。

正式地說，圖是一對集合(V, E)，其中V是頂點的集合，E是連線頂點對的邊的集合。請看下面的圖：

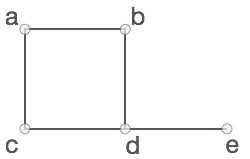
Graph Basics

在上圖中，

V = {a, b, c, d, e}

E = {ab, ac, bd, cd, de}

圖資料結構

數學圖可以用資料結構表示。我們可以使用頂點陣列和二維邊陣列來表示圖。在我們繼續之前，讓我們熟悉一些重要的術語：

  • 頂點 - 圖的每個節點都表示為一個頂點。在下面的例子中，帶標籤的圓圈代表頂點。因此，A到G都是頂點。我們可以用陣列來表示它們，如下圖所示。這裡A可以用索引0標識，B可以用索引1標識，以此類推。

  • 邊 - 邊表示兩個頂點之間的路徑或兩點之間的線。在下面的例子中，從A到B、B到C等的線表示邊。我們可以使用二維陣列來表示陣列，如下圖所示。這裡AB可以用第0行第1列的1表示，BC可以用第1行第2列的1表示，以此類推，其他組合保持為0。

  • 鄰接 - 如果兩個節點或頂點透過一條邊相互連線，則它們是鄰接的。在下面的例子中，B與A鄰接，C與B鄰接，以此類推。

  • 路徑 - 路徑表示兩個頂點之間的一系列邊。在下面的例子中，ABCD表示從A到D的路徑。

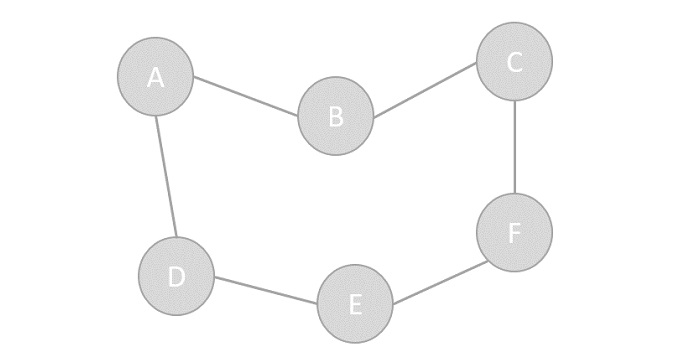
graph graph

圖的操作

圖的主要操作包括建立一個帶有頂點和邊的圖，以及顯示該圖。但是，使用圖執行的最常見和最流行的操作之一是遍歷，即以特定順序訪問圖的每個頂點。

圖中有兩種型別的遍歷：

深度優先搜尋遍歷

深度優先搜尋是一種遍歷演算法，它按照其深度的遞減順序訪問圖的所有頂點。在這個演算法中，選擇一個任意節點作為起點，透過標記未訪問的鄰接節點來回遍歷圖，直到所有頂點都被標記。

DFS遍歷使用棧資料結構來跟蹤未訪問的節點。

點選檢視 深度優先搜尋遍歷

廣度優先搜尋遍歷

廣度優先搜尋是一種遍歷演算法，它在移動到下一層深度之前訪問圖中同一層深度上存在的所有頂點。在這個演算法中，選擇一個任意節點作為起點，透過訪問同一深度級別上的鄰接頂點並標記它們來遍歷圖，直到沒有剩餘頂點。

DFS遍歷使用佇列資料結構來跟蹤未訪問的節點。

點選檢視 廣度優先搜尋遍歷

圖的表示

在表示圖時，我們必須仔細描繪圖中存在的元素（頂點和邊）以及它們之間的關係。圖解地，圖用有限的節點集和它們之間的連線連結來表示。但是，我們也可以用其他最常用的方式表示圖，例如：

  • 鄰接矩陣

  • 鄰接表

鄰接矩陣

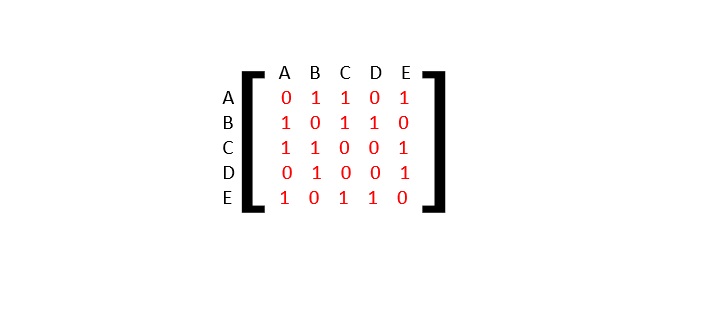
鄰接矩陣是一個 V x V 矩陣，其值填充為 0 或 1。如果 Vi 和 Vj 之間存在連結，則記錄為 1；否則為 0。

對於下面給定的圖，讓我們構造一個鄰接矩陣：

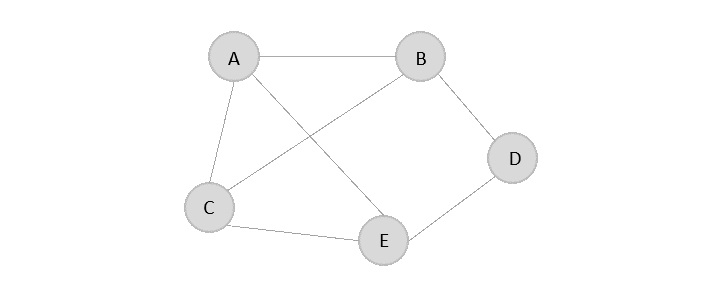
Adjacency_Matrix

鄰接矩陣是：

adjacency_matrix

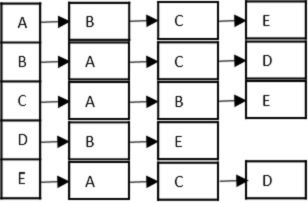
鄰接表

鄰接表是直接連線到圖中其他頂點的頂點的列表。

Adjacency_Matrix

鄰接表是：

adjacency list

圖的型別

圖主要有兩種型別：

  • 有向圖

  • 無向圖

顧名思義，有向圖由具有方向的邊組成，這些方向要麼遠離頂點，要麼指向頂點。無向圖的邊完全沒有方向。

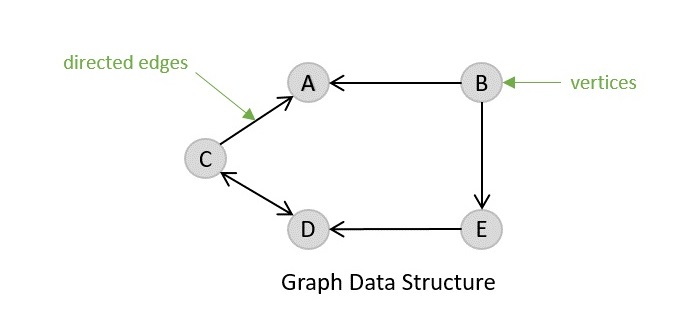
Directed Graph

有向圖

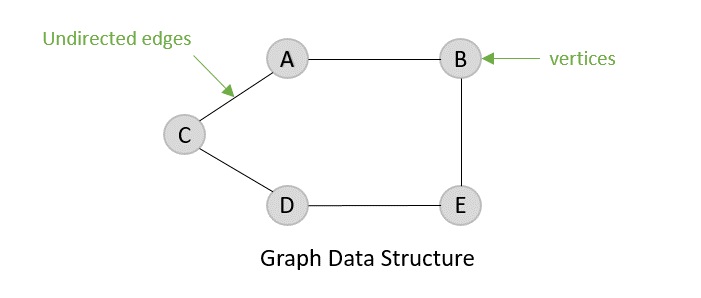
Undirected_Grap

無向圖

生成樹

一個生成樹是無向圖的子集，它包含以圖中最小數量的邊連線在一起的圖的所有頂點。精確地說，生成樹的邊是原始圖中邊的子集。

如果圖中的所有頂點都連線在一起，則至少存在一個生成樹。在一個圖中，可能存在多個生成樹。

屬性

  • 生成樹沒有任何環。

  • 可以從任何其他頂點到達任何頂點。

示例

在下圖中，突出顯示的邊構成一個生成樹。

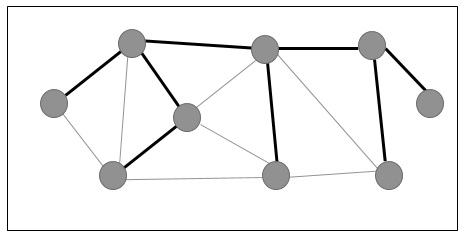
Spanning Tree

最小生成樹

最小生成樹 (MST) 是連線加權無向圖的所有頂點的邊的一個子集，其總邊權重最小。要匯出 MST，可以使用 Prim 演算法或 Kruskal 演算法。因此，我們將在本章中討論 Prim 演算法。

正如我們所討論的，一個圖可能有多個生成樹。如果有 n 個頂點，則生成樹應具有 n − 1 個邊。在這種情況下，如果圖的每條邊都與權重相關聯，並且存在多個生成樹，我們需要找到圖的最小生成樹。

此外，如果存在任何重複的加權邊，則該圖可能具有多個最小生成樹。

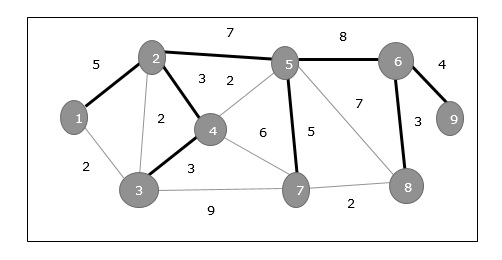
Minimum Spanning Tree

在上圖中，我們顯示了一個生成樹，儘管它不是最小生成樹。此生成樹的成本為(5+7+3+3+5+8+3+4)=38。

最短路徑

圖中的最短路徑定義為從一個頂點到另一個頂點的最小成本路線。這在加權有向圖中最常見，但也適用於無向圖。

在圖中尋找最短路徑的一個常見實際應用是地圖導航。藉助各種最短路徑演算法，目的地被視為圖的頂點，路線被視為邊，這使得導航更加輕鬆便捷。兩種常用的最短路徑演算法是：

  • 迪傑斯特拉最短路徑演算法 (Dijkstra's Shortest Path Algorithm)

  • 貝爾曼-福特最短路徑演算法 (Bellman-Ford's Shortest Path Algorithm)

示例

以下是該操作在各種程式語言中的實現：

C語言 C++ Java Python
#include <stdio.h>
#include <stdlib.h>
#include <stdlib.h>
#define V 5 

// Maximum number of vertices in the graph
struct graph { 
   
   // declaring graph data structure
   struct vertex *point[V];
};
struct vertex { 
   
   // declaring vertices
   int end;
   struct vertex *next;
};
struct Edge { 
   
   // declaring edges
   int end, start;
};
struct graph *create_graph (struct Edge edges[], int x){
   int i;
   struct graph *graph = (struct graph *) malloc (sizeof (struct graph));
   for (i = 0; i < V; i++) {
      graph->point[i] = NULL;
   }
   for (i = 0; i < x; i++) {
      int start = edges[i].start;
      int end = edges[i].end;
      struct vertex *v = (struct vertex *) malloc (sizeof (struct vertex));
      v->end = end;
      v->next = graph->point[start];
      graph->point[start] = v;
   }
   return graph;
}
int main (){
   struct Edge edges[] = { {0, 1}, {0, 2}, {0, 3}, {1, 2}, {1, 4}, {2, 4}, {2, 3}, {3, 1} };
   int n = sizeof (edges) / sizeof (edges[0]);
   struct graph *graph = create_graph (edges, n);
   printf("The graph created is: ");
   for (int i = 0; i < V; i++) {
      struct vertex *ptr = graph->point[i];
      while (ptr != NULL) {
         printf ("(%d -> %d)\t", i, ptr->end);
         ptr = ptr->next;
      }
      printf ("\n");
   }
   return 0;
}

輸出

The graph created is:
(1 -> 3)	(1 -> 0)	
(2 -> 1)	(2 -> 0)	
(3 -> 2)	(3 -> 0)	
(4 -> 2)	(4 -> 1)	

#include <bits/stdc++.h>
using namespace std;
#define V 5 

// Maximum number of vertices in the graph
struct graph { 
   
   // declaring graph data structure
   struct vertex *point[V];
};
struct vertex { 
   
   // declaring vertices
   int end;
   struct vertex *next;
};
struct Edge { 
   
   // declaring edges
   int end, start;
};
struct graph *create_graph (struct Edge edges[], int x){
   int i;
   struct graph *graph = (struct graph *) malloc (sizeof (struct graph));
   for (i = 0; i < V; i++) {
      graph->point[i] = NULL;
   }
   for (i = 0; i < x; i++) {
      int start = edges[i].start;
      int end = edges[i].end;
      struct vertex *v = (struct vertex *) malloc (sizeof (struct vertex));
      v->end = end;
      v->next = graph->point[start];
      graph->point[start] = v;
   }
   return graph;
}
int main (){
   struct Edge edges[] = { {0, 1}, {0, 2}, {0, 3}, {1, 2}, {1, 4}, {2, 4}, {2, 3}, {3, 1} };
   int n = sizeof (edges) / sizeof (edges[0]);
   struct graph *graph = create_graph (edges, n);
   int i;
   cout<<"The graph created is: ";
   for (i = 0; i < V; i++) {
      struct vertex *ptr = graph->point[i];
      while (ptr != NULL) {
         cout << "(" << i << " -> " << ptr->end << ")\t";
         ptr = ptr->next;
      }
      cout << endl;
   }
   return 0;
}

輸出

The graph created is: 
(1 -> 3)	(1 -> 0)	
(2 -> 1)	(2 -> 0)	
(3 -> 2)	(3 -> 0)	
(4 -> 2)	(4 -> 1)

import java.util.*;

//class to store edges of the graph
class Edge {   
   int src, dest;
   Edge(int src, int dest) {
      this.src = src;
      this.dest = dest;
   }
}

// Graph class
public class Graph {
   
   // node of adjacency list
   static class vertex {
      int v;
      vertex(int v) {
        this.v = v;
      }
   };
   // define adjacency list to represent the graph
   List<List<vertex>> adj_list = new ArrayList<>();
   
   //Graph Constructor
   public Graph(List<Edge> edges){
      
      // adjacency list memory allocation
      for (int i = 0; i < edges.size(); i++)
      adj_list.add(i, new ArrayList<>());
      
      // add edges to the graph
      for (Edge e : edges){
        
        // allocate new node in adjacency List from src to dest
        adj_list.get(e.src).add(new vertex(e.dest));
      }
   }
   public static void main (String[] args) {
      
      // define edges of the graph
      List<Edge> edges = Arrays.asList(new Edge(0, 1),new Edge(0, 2),
      new Edge(0, 3),new Edge(1, 2), new Edge(1, 4),
      new Edge(2, 4), new Edge(2, 3),new Edge(3, 1));
      
      // call graph class Constructor to construct a graph
      Graph graph = new Graph(edges);
      
      // print the graph as an adjacency list
      int src = 0;
      int lsize = graph.adj_list.size();
      System.out.println("The graph created is: ");
      while (src < lsize) {
      
         //traverse through the adjacency list and print the edges
         for (vertex edge : graph.adj_list.get(src)) {
            System.out.print(src + " -> " + edge.v + "\t");
         }
         System.out.println();
         src++;
      }
   }
}

輸出

The graph created is: 
0 -> 1	0 -> 2	0 -> 3	
1 -> 2	1 -> 4	
2 -> 4	2 -> 3	
3 -> 1

#Python code for Graph Data Struture
V = 5
#Maximum number of vertices in th graph
#Declaring vertices
class Vertex:
    def __init__(self, end):
        self.end = end
        self.next = None
#Declaring Edges
class Edge:
    def __init__(self, start, end):
        self.start = start
        self.end = end
#Declaring graph data structure
class Graph:
    def __init__(self):
        self.point = [None] * V
def create_graph(edges, x):
    graph = Graph()
    for i in range(V):
        graph.point[i] = None
    for i in range(x):
        start = edges[i].start
        end = edges[i].end
        v = Vertex(end)
        v.next = graph.point[start]
        graph.point[start] = v
    return graph
edges = [Edge(0, 1), Edge(0, 2), Edge(0, 3), Edge(1, 2), Edge(1, 4), Edge(2, 4), Edge(2, 3), Edge(3, 1)]
n = len(edges)
graph = create_graph(edges, n)
#Range
print("The graph created is: ")
for i in range(V):
    ptr = graph.point[i]
    while ptr is not None:
        print("({} -> {})".format(i, ptr.end), end="\t")
        ptr = ptr.next
    print()

輸出

The graph created is: 
(0 -> 3)	(0 -> 2)	(0 -> 1)	
(1 -> 4)	(1 -> 2)	
(2 -> 3)	(2 -> 4)	
(3 -> 1)
列印頁面
上一頁
下一頁
廣告