漢諾塔問題（使用遞迴）

Table of content

漢諾塔
規則
演算法
示例

漢諾塔

漢諾塔是一個數學遊戲，由三個塔（樁）和多個環組成，如下圖所示：

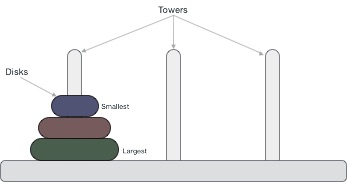
這些環大小不同，按升序排列堆疊，即較小的環放在較大的環上面。該遊戲的其他變體中，圓盤的數量會增加，但塔的數量保持不變。

規則

任務是將所有圓盤移動到另一個塔，而不違反排列順序。漢諾塔遊戲需要遵循以下規則：

在任何給定時間，只能在塔之間移動一個圓盤。
只能移動“頂部”的圓盤。
較大的圓盤不能放在較小的圓盤上面。

以下是使用三個圓盤解決漢諾塔遊戲的動畫演示。

包含 n 個圓盤的漢諾塔遊戲最少需要 2ⁿ−1 步才能解決。此演示顯示，包含 3 個圓盤的遊戲需要 2³ - 1 = 7 步。

演算法

要編寫漢諾塔遊戲的演算法，首先我們需要學習如何使用較少的圓盤（例如 1 或 2）來解決此問題。我們將三個塔分別命名為源、目標和輔助（僅用於幫助移動圓盤）。如果只有一個圓盤，則可以輕鬆地將其從源塔移動到目標塔。

如果有 2 個圓盤：

首先，我們將較小的（頂部）圓盤移動到輔助塔。
然後，我們將較大的（底部）圓盤移動到目標塔。
最後，我們將較小的圓盤從輔助塔移動到目標塔。

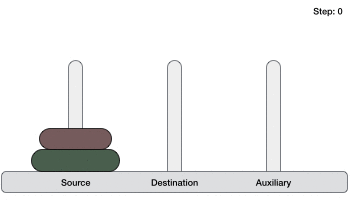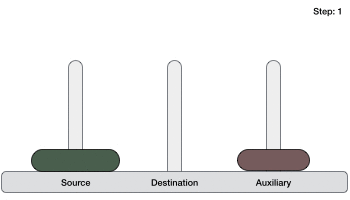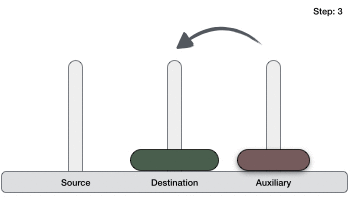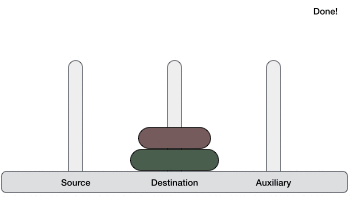
因此，現在我們可以設計一個用於解決包含兩個以上圓盤的漢諾塔遊戲的演算法。我們將圓盤堆疊分成兩部分。最大的圓盤（第 n 個圓盤）在一部分，所有其他（n-1）個圓盤在另一部分。

我們的最終目標是從源塔將第 n 個圓盤移動到目標塔，然後將所有其他（n-1）個圓盤放在它上面。我們可以想象以遞迴的方式對所有給定的圓盤集應用相同的操作。

需要遵循的步驟：

Step 1 − Move n-1 disks from source to aux
Step 2 − Move n^th disk from source to dest
Step 3 − Move n-1 disks from aux to dest

漢諾塔遊戲的遞迴演算法可以如下所示：

START
Procedure Hanoi(disk, source, dest, aux)

   IF disk == 1, THEN
      move disk from source to dest             
   ELSE
      Hanoi(disk - 1, source, aux, dest)     // Step 1
      move disk from source to dest          // Step 2
      Hanoi(disk - 1, aux, dest, source)     // Step 3
   END IF
   
END Procedure
STOP

示例

以下是此方法在各種程式語言中的實現：

C C++ Java Python

#include <stdio.h>
void hanoi(int n, char from, char to, char via) {
   if(n == 1){
      printf("Move disk 1 from %c to %c\n", from, to);
   }
   else{
      hanoi(n-1, from, via, to);
      printf("Move disk %d from %c to %c\n", n, from, to);
      hanoi(n-1, via, to, from);
   }
}
int main() {
   int n = 3;
   char from = 'A';
   char to = 'B';
   char via = 'C';
   //calling hanoi() method
   hanoi(n, from, via, to);
}

#include <iostream>
using namespace std;
void hanoi(int n, char from, char to, char via) {
   if(n == 1){
      cout<<"Move disk 1 from "<<from<<" to "<<to<<endl;
   }
   else{
      hanoi(n-1, from, via, to);
      cout<<"Move disk "<<n<<" from "<<from<<" to "<<to<<endl;
      hanoi(n-1, via, to, from);
   }
}
int main() {
   int n = 3;
   char from = 'A';
   char to = 'B';
   char via = 'C';
   //calling hanoi() method
   hanoi(n, from , via, to);
}

import java.util.*;
public class Demo {
   public static void hanoi(int n, String from, String to, String via) {
      if(n == 1){
         System.out.println("Move disk 1 from " + from + " to " + to);
      }
      else{
         hanoi(n-1, from, via, to);
         System.out.println("Move disk " + n + " from " + from + " to " + to);
         hanoi(n-1, via, to, from);
      }
   }
   public static void main(String[] args) {
      int n = 3;
      String from = "A";
      String to = "B";
      String via = "C";
      //calling hanoi() metod
      hanoi(n, from, via, to);
   }
}

def hanoi(n, f, to, via):
    if n == 1:
        print("Move disk 1 from",f,"to",to);
    else:
        hanoi(n-1, f, via, to)
        print("Move disk",n,"from",f,"to",to);
        hanoi(n-1, via, to, f)
n = 3
f = 'A'
to = 'B'
via = 'C'
hanoi(n, f, via, to)

輸出

Move disk 1 from A to C
Move disk 2 from A to B
Move disk 1 from C to B
Move disk 3 from A to C
Move disk 1 from B to A
Move disk 2 from B to C
Move disk 1 from A to C

列印頁面