頂點覆蓋演算法

Table of content
上一個
下一個

你有沒有想過交通攝像頭的擺放位置？以及它們如何在不浪費政府過多預算的情況下高效地放置？答案以**頂點覆蓋演算法**的形式出現。攝像頭的放置位置以一種方式選擇，即一個攝像頭覆蓋儘可能多的道路，也就是說，我們選擇路口並確保攝像頭覆蓋儘可能大的區域。

無向圖**G = (V,E)**的**頂點覆蓋**是指圖的頂點子集，使得對於圖中的所有邊**（u,v）**，**u 和 v ∈ V**。路口被視為圖的節點，道路被視為邊。該演算法找到覆蓋最大數量道路的最小路口集。

這是一個最小化問題，因為我們找到頂點覆蓋的最小大小——頂點覆蓋的大小是其中的頂點數。最佳化問題是一個NP完全問題，因此不能在多項式時間內解決；但可以在多項式時間內找到的是近似最優解。

頂點覆蓋演算法

頂點覆蓋近似演算法以無向圖作為輸入，並執行以獲得一組頂點，該頂點的數量肯定是不小於最優頂點覆蓋的兩倍。

頂點覆蓋是一個2-近似演算法。

演算法

**步驟1** - 從輸入圖中選擇任意一條邊，並標記與該邊對應的頂點相關聯的所有邊。

**步驟2** - 將任意邊的頂點新增到輸出集中。

**步驟3** - 對圖中剩餘的未標記邊重複步驟1，並將選擇的頂點新增到輸出中，直到沒有未標記的邊。

**步驟4** - 最終得到的輸出集將是近似最優的頂點覆蓋。

虛擬碼

APPROX-VERTEX_COVER (G: Graph)
c ← { }
E’ ← E[G]
while E’ is not empty do
   Let (u, v) be an arbitrary edge of E’
   c ← c U {u, v}
   Remove from E’ every edge incident on either u or v
return c

示例

給定圖的邊集為：

{(1,6),(1,2),(1,4),(2,3),(2,4),(6,7),(4,7),(7,8),(3,5),(8,5)}
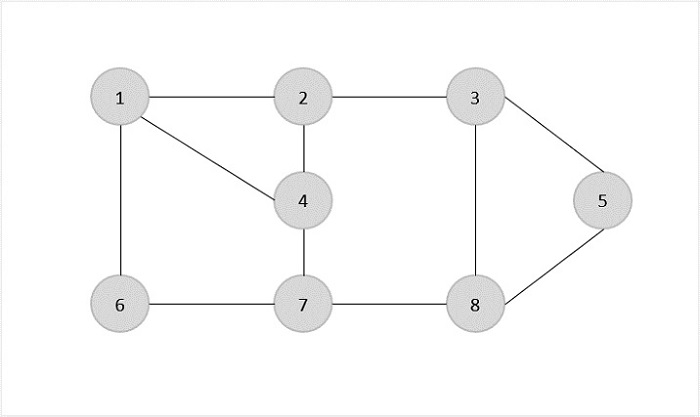
Vertex_Cover_Problem

現在，我們從選擇任意邊（1,6）開始。我們消去所有與頂點1或6相關聯的邊，並將邊（1,6）新增到覆蓋中。

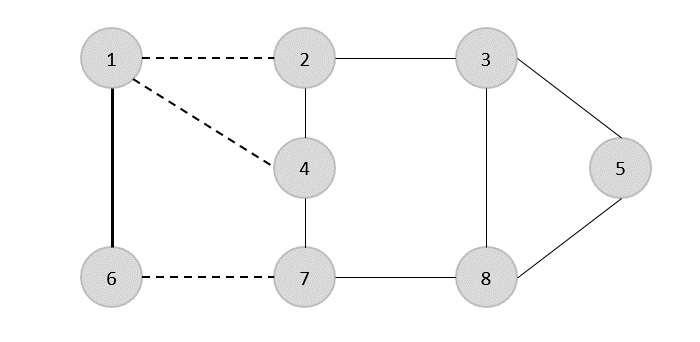
arbitrary_edge

在下一步中，我們隨機選擇了另一條邊（2,3）。

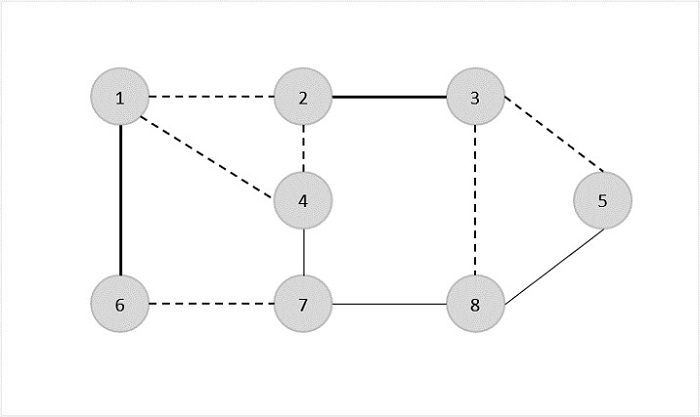
chosen_another_edge

現在我們選擇另一條邊（4,7）。

select_another_edge

我們選擇另一條邊（8,5）。

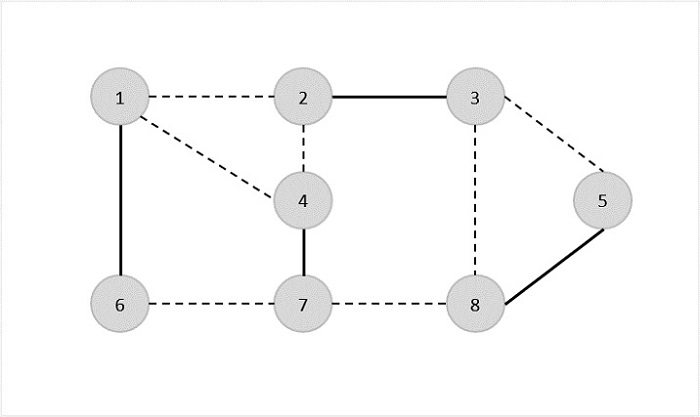
another edge 8 to 5

因此，該圖的頂點覆蓋為{1,6,2,3,4,7,5,8}。

分析

很容易看出該演算法的執行時間為O(V + E)，使用鄰接表來表示E'。

實現

以下是上述方法在各種程式語言中的實現：

C C++ Java Python
#include <stdio.h>
#include <stdbool.h>
#define MAX_VERTICES 100
int graph[MAX_VERTICES][MAX_VERTICES];
bool included[MAX_VERTICES];
// Function to find Vertex Cover using the APPROX-VERTEX_COVER algorithm
void approxVertexCover(int vertices, int edges) {
   bool edgesRemaining[MAX_VERTICES][MAX_VERTICES];
   for (int i = 0; i < vertices; i++) {
      for (int j = 0; j < vertices; j++) {
         edgesRemaining[i][j] = graph[i][j];
      }
   }
   while (edges > 0) {
      int u, v;
      for (int i = 0; i < vertices; i++) {
         for (int j = 0; j < vertices; j++) {
            if (edgesRemaining[i][j]) {
               u = i;
               v = j;
               break;
            }
         }
      }
      included[u] = included[v] = true;
      for (int i = 0; i < vertices; i++) {
         edgesRemaining[u][i] = edgesRemaining[i][u] = false;
         edgesRemaining[v][i] = edgesRemaining[i][v] = false;
      }
      edges--;
   }
}
int main() {
   int vertices = 8;
   int edges = 10;
   int edgesData[10][2] = {
   {1, 6}, {1, 2}, {1, 4}, {2, 3}, {2, 4},
   {6, 7}, {4, 7}, {7, 8}, {3, 5}, {8, 5}};
   for (int i = 0; i < edges; i++) {
      int u = edgesData[i][0];
      int v = edgesData[i][1];
      graph[u][v] = graph[v][u] = 1;
   }
   approxVertexCover(vertices, edges);
   printf("Vertex Cover: ");
   for (int i = 1; i <= vertices; i++) {
      if (included[i]) {
         printf("%d ", i);
      }
   }
   printf("\n");
   return 0;
}

輸出

Vertex Cover: 1 3 4 5 6 7 

#include <iostream>
#include <vector>
using namespace std;
const int MAX_VERTICES = 100;
vector<vector<int>> graph(MAX_VERTICES, vector<int>(MAX_VERTICES, 0));
vector<bool> included(MAX_VERTICES, false);
// Function to find Vertex Cover using the APPROX-VERTEX_COVER algorithm
void approxVertexCover(int vertices, int edges) {
   vector<vector<bool>> edgesRemaining(vertices, vector<bool>(vertices, false));
   for (int i = 0; i < vertices; i++) {
      for (int j = 0; j < vertices; j++) {
         edgesRemaining[i][j] = graph[i][j];
      }
   }
   while (edges > 0) {
      int u, v;
      for (int i = 0; i < vertices; i++) {
         for (int j = 0; j < vertices; j++) {
            if (edgesRemaining[i][j]) {
               u = i;
               v = j;
               break;
            }
         }
      }
      included[u] = included[v] = true;
      for (int i = 0; i < vertices; i++) {
         edgesRemaining[u][i] = edgesRemaining[i][u] = false;
         edgesRemaining[v][i] = edgesRemaining[i][v] = false;
      }
      edges--;
   }
}
int main() {
   int vertices = 8;
   int edges = 10;
   int edgesData[10][2] = {
   {1, 6}, {1, 2}, {1, 4}, {2, 3}, {2, 4},
   {6, 7}, {4, 7}, {7, 8}, {3, 5}, {8, 5}};
   for (int i = 0; i < edges; i++) {
      int u = edgesData[i][0];
      int v = edgesData[i][1];
      graph[u][v] = graph[v][u] = 1;
   }
   approxVertexCover(vertices, edges);
   cout << "Vertex Cover: ";
   for (int i = 1; i <= vertices; i++) {
      if (included[i]) {
         cout << i << " ";
      }
   }
   cout << endl;
   return 0;
}

輸出

Vertex Cover: 1 3 4 5 6 7 

import java.util.ArrayList;
import java.util.List;
public class Main {
   static final int MAX_VERTICES = 100;
   static int[][] graph = new int[MAX_VERTICES][MAX_VERTICES];
   static boolean[] included = new boolean[MAX_VERTICES];
   public static void approx_vertex_cover(int vertices, int edges) {
      int[][] edges_remaining = new int[MAX_VERTICES][MAX_VERTICES];
      for (int i = 0; i < vertices; i++) {
         for (int j = 0; j < vertices; j++) {
            edges_remaining[i][j] = graph[i][j];
         }
      }
      while (edges > 0) {
         int u = 1, v = 1;
         for (int i = 0; i < vertices; i++) {
            for (int j = 0; j < vertices; j++) {
               if (edges_remaining[i][j] != 0) {
                  u = i;
                  v = j;
                  break;
               }
            }
         }
         included[u] = included[v] = true;
         for (int i = 0; i < vertices; i++) {
            edges_remaining[u][i] = edges_remaining[i][u] = 0;
            edges_remaining[v][i] = edges_remaining[i][v] = 0;
         }
         edges--;
    }
}
public static void main(String[] args) {
   int vertices = 8;
   int edges = 10;
   List<int[]> edges_data = new ArrayList<>();
   edges_data.add(new int[] {1, 6});
   edges_data.add(new int[] {1, 2});
   edges_data.add(new int[] {1, 4});
   edges_data.add(new int[] {2, 3});
   edges_data.add(new int[] {2, 4});
   edges_data.add(new int[] {6, 7});
   edges_data.add(new int[] {4, 7});
   edges_data.add(new int[] {7, 8});
   edges_data.add(new int[] {3, 5});
   edges_data.add(new int[] {8, 5});
   for (int[] edge : edges_data) {
      int u = edge[0];
      int v = edge[1];
      graph[u][v] = graph[v][u] = 1;
}
approx_vertex_cover(vertices, edges);
System.out.print("Vertex Cover: ");
for (int i = 1; i <= vertices; i++) {
   if (included[i]) {
      System.out.print(i + " ");
   }
}
System.out.println();
}
}

輸出

Vertex Cover: 1 3 4 5 6 7 

MAX_VERTICES = 100
graph = [[0 for _ in range(MAX_VERTICES)] for _ in range(MAX_VERTICES)]
included = [False for _ in range(MAX_VERTICES)]
# Function to find Vertex Cover using the APPROX-VERTEX_COVER algorithm
def approx_vertex_cover(vertices, edges):
    edges_remaining = [row[:] for row in graph]
    while edges > 0:
        for i in range(vertices):
            for j in range(vertices):
                if edges_remaining[i][j]:
                    u = i
                    v = j
                    break
        included[u] = included[v] = True
        for i in range(vertices):
            edges_remaining[u][i] = edges_remaining[i][u] = False
            edges_remaining[v][i] = edges_remaining[i][v] = False
        edges -= 1
if __name__ == "__main__":
    vertices = 8
    edges = 10
    edges_data = [(1, 6), (1, 2), (1, 4), (2, 3), (2, 4),
                  (6, 7), (4, 7), (7, 8), (3, 5), (8, 5)]
    for u, v in edges_data:
        graph[u][v] = graph[v][u] = 1
    approx_vertex_cover(vertices, edges)
    print("Vertex Cover:", end=" ")
    for i in range(1, vertices + 1):
        if included[i]:
            print(i, end=" ")
    print()

輸出

Vertex Cover: 1 3 4 5 6 7
列印頁面
上一個
下一個
廣告