隨機演算法

隨機演算法是一種與標準演算法不同的設計方法，它在演算法邏輯的某些部分添加了一些隨機位元。它們與確定性演算法不同；確定性演算法遵循確定的程式，每次輸入都會得到相同的輸出，而隨機演算法每次執行都會產生不同的輸出。需要注意的是，隨機的不是輸入，而是標準演算法的邏輯。

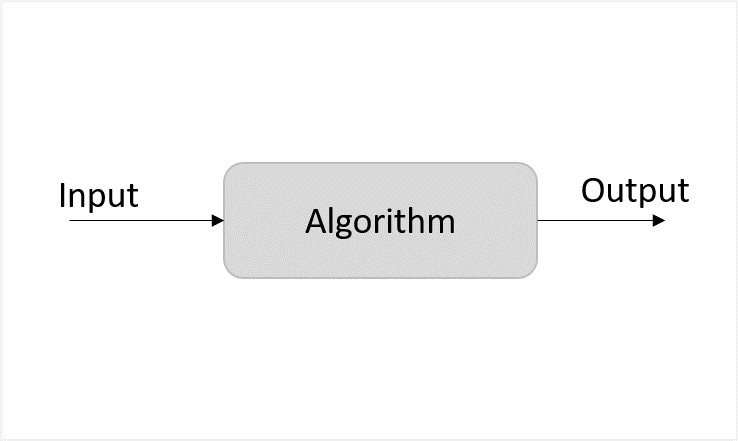
圖1：確定性演算法

與確定性演算法不同，隨機演算法除了考慮輸入外，還考慮邏輯中的隨機位元，這些位元反過來有助於獲得輸出。

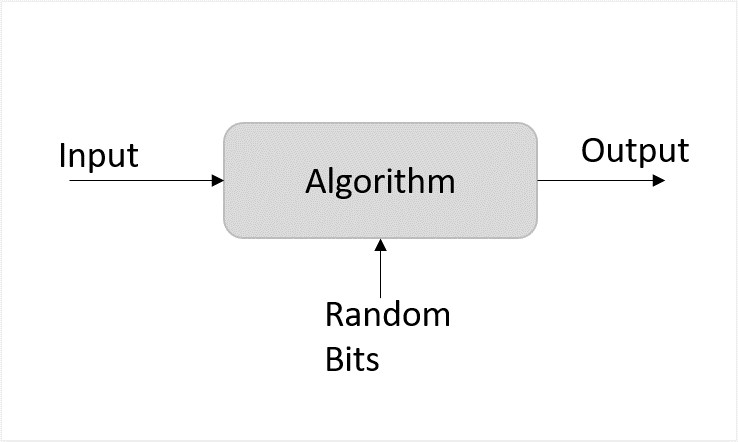
圖2：隨機演算法

然而，也不能排除隨機演算法產生錯誤輸出的可能性。因此，執行稱為**放大**的過程以減少這些錯誤輸出的可能性。放大也是一種演算法，它用於多次執行隨機演算法的某些部分以提高正確性的機率。然而，過多的放大也會超過時間限制，使演算法無效。

隨機演算法的分類

隨機演算法根據其時間約束是隨機變數還是確定性值進行分類。它們以兩種常見形式設計——拉斯維加斯和蒙特卡洛。

• **拉斯維加斯**——拉斯維加斯方法的隨機演算法永遠不會給出錯誤的輸出，這使得時間約束成為隨機變數。例如，在字串匹配演算法中，拉斯維加斯演算法一旦遇到錯誤就從頭開始。這增加了正確性的機率。例如，隨機快速排序演算法。

• **蒙特卡羅**——蒙特卡羅方法的隨機演算法專注於在給定的時間約束內完成執行。因此，此方法的執行時間是確定的。例如，在字串匹配中，如果蒙特卡羅遇到錯誤，它會從同一點重新啟動演算法。從而節省時間。例如，Karger最小割演算法

隨機演算法的必要性

這種方法通常用於降低時間複雜度和空間複雜度。但對於新增隨機性如何降低執行時間和儲存記憶體而不是增加，可能存在一些模糊之處；我們將使用博弈論來理解這一點。

博弈論與隨機演算法

博弈論的基本思想實際上提供了一些模型，這些模型有助於理解遊戲中的決策者如何相互作用。這些博弈論模型使用假設來確定遊戲中參與者的決策結構。這些理論模型做出的流行假設是，參與者都是理性的，並且會考慮對手在特定遊戲情況下會做出什麼決定。我們將把這個理論應用於隨機演算法。

零和博弈

零和博弈是博弈論的數學表示。它有兩個參與者，結果對一個參與者是收益，而對另一個參與者是等值的損失。因此，淨改進是兩個參與者狀態的總和，總和為零。

隨機演算法基於設計一種演算法的零和博弈，該演算法對所有輸入都具有最低的時間複雜度。遊戲中有兩個參與者；一個設計算法，另一個為演算法提供輸入。玩家二需要以這樣一種方式提供輸入，即它將產生最壞的時間複雜度以贏得遊戲。而玩家一需要設計一種演算法，該演算法執行任何給定輸入所需的時間最短。

例如，考慮快速排序演算法，其中主演算法從選擇樞軸元素開始。但是，如果零和博弈中的玩家選擇排序列表作為輸入，則標準演算法會提供最壞情況下的時間複雜度。因此，隨機化樞軸選擇將比最壞時間複雜度更快地執行演算法。但是，即使演算法隨機選擇第一個元素作為樞軸並獲得最壞的時間複雜度，使用相同的輸入再次執行它也會解決問題，因為它這次會選擇另一個樞軸。

另一方面，對於像歸併排序這樣的演算法，時間複雜度不依賴於輸入；即使演算法是隨機的，時間複雜度也會保持不變。因此，**隨機化僅應用於複雜度取決於輸入的演算法**。

示例

隨機演算法的一些流行示例是：

• 隨機快速排序演算法

• Karger最小割演算法

• Fisher-Yates洗牌演算法

• 子集和問題