佇列資料結構

上一頁
下一頁

什麼是佇列？

佇列是一種線性資料結構，其中元素按照 FIFO（先進先出）原則儲存，即第一個插入的元素將是第一個被訪問的元素。佇列是一種抽象資料型別（ADT），類似於棧，使佇列與棧不同的特點是佇列的兩端都是開放的。資料透過一端插入佇列，並透過另一端從佇列中刪除。佇列在大多數程式語言中被頻繁使用。

car

佇列的一個現實世界例子可以是一條單車道單行道，其中先進入的車輛先退出。在售票視窗和公交車站的佇列也可以看到更多現實世界的例子。

佇列的表示

與棧 ADT 類似，佇列 ADT 也可以使用陣列、連結串列或指標來實現。在本教程中，我們以一個小例子為例，使用一維陣列實現佇列。

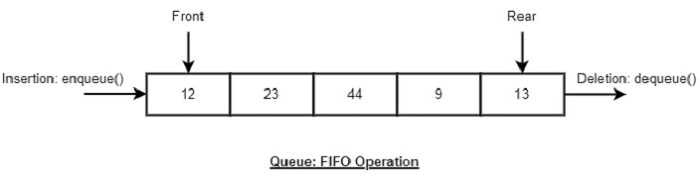
Representation of queues

佇列的基本操作

佇列操作還包括佇列的初始化、使用以及從記憶體中永久刪除資料。

佇列 ADT 中最基本的操作包括：enqueue()、dequeue()、peek()、isFull()、isEmpty()。這些都是內建操作，用於執行資料操作和檢查佇列的狀態。

佇列使用兩個指標 - front 和 rear。front 指標從前端訪問資料（幫助入隊），而 rear 指標從後端訪問資料（幫助出隊）。

佇列插入操作：Enqueue()

enqueue() 是一種資料操作，用於將元素插入棧中。以下演算法以更簡單的方式描述了 enqueue() 操作。

演算法

1. START
2. Check if the queue is full.
3. If the queue is full, produce overflow error and exit.
4. If the queue is not full, increment rear pointer to point 
   the next empty space.
5. Add data element to the queue location, where the rear 
   is pointing.
6. return success.
7. END

示例

以下是此操作在各種程式語言中的實現 -

C C++ Java Python
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
bool isFull(){
   return itemCount == MAX;
}
bool isEmpty(){
   return itemCount == 0;
}
int removeData(){
   int data = intArray[front++];
   if(front == MAX) {
      front = 0;
   }
   itemCount--;
   return data;
}
void insert(int data){
   if(!isFull()) {
      if(rear == MAX-1) {
         rear = -1;
      }
      intArray[++rear] = data;
      itemCount++;
   }
}
int main(){
   insert(3);
   insert(5);
   insert(9);
   insert(1);
   insert(12);
   insert(15);
   printf("Queue: ");
   while(!isEmpty()) {
      int n = removeData();
      printf("%d ",n);
   }
}

輸出

Queue: 3 5 9 1 12 15

#include <iostream>
#include <string>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
bool isFull(){
   return itemCount == MAX;
}
bool isEmpty(){
   return itemCount == 0;
}
int removeData(){
   int data = intArray[front++];
   if(front == MAX) {
      front = 0;
   }
   itemCount--;
   return data;
}
void insert(int data){
   if(!isFull()) {
      if(rear == MAX-1) {
         rear = -1;
      }
      intArray[++rear] = data;
      itemCount++;
   }
}
int main(){
   insert(3);
   insert(5);
   insert(9);
   insert(1);
   insert(12);
   insert(15);
   printf("Queue: ");
   while(!isEmpty()) {
      int n = removeData();
      printf("%d ",n);
   }
}

輸出

Queue: 3 5 9 1 12 15

import java.util.*;
public class Demo{
static final int MAX = 6;
static int intArray[] = new int[MAX];
static int front = 0;
static int rear = -1;
static int itemCount = 0;
public static boolean isFull(){
   return itemCount == MAX;
}
public static boolean isEmpty(){
   return itemCount == 0;
}
public static int removeData(){
   int data = intArray[front++];
   if(front == MAX) {
      front = 0;
   }
   itemCount--;
   return data;
}
public static void insert(int data){
   if(!isFull()) {
      if(rear == MAX-1) {
         rear = -1;
      }
      intArray[++rear] = data;
      itemCount++;
   }
}
public static void main(String[] args){
   insert(3);
   insert(5);
   insert(9);
   insert(1);
   insert(12);
   insert(15);
   System.out.print("Queue: ");
   while(!isEmpty()) {
      int n = removeData();
      System.out.print(n + " ");
   }
  }
}

輸出

Queue: 3 5 9 1 12 15 

MAX = 6;
intArray = [0] * MAX
front = 0;
rear = -1;
itemCount = 0;
def isFull():
    return itemCount == MAX
def isEmpty():
    return itemCount == 0
def removeData():
    data = intArray[front+1]
    if(front == MAX):
        front = 0
    itemCount-1
    return data
def insert(data):
    global rear, itemCount
    if(not isFull()):
        if(rear == MAX-1):
            rear = -1
        rear = rear + 1
        intArray[rear] = data
        itemCount+1
insert(3);
insert(5);
insert(9);
insert(1);
insert(12);
insert(15);
print("Queue: ")
for i in range(MAX):
    print(intArray[i], end = " ")
while(not isEmpty()):
    n = removeData()
    print(n, end = " ")

輸出

Queue: 
3 5 9 1 12 15

佇列刪除操作：dequeue()

dequeue() 是一種資料操作，用於從棧中刪除元素。以下演算法以更簡單的方式描述了 dequeue() 操作。

演算法

1. START
2. Check if the queue is empty.
3. If the queue is empty, produce underflow error and exit.
4. If the queue is not empty, access the data where front 
   is pointing.
5. Increment front pointer to point to the next available 
   data element.
6. Return success.
7. END

示例

以下是此操作在各種程式語言中的實現 -

C C++ Java Python
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
bool isFull(){
   return itemCount == MAX;
}
bool isEmpty(){
   return itemCount == 0;
}
void insert(int data){
   if(!isFull()) {
      if(rear == MAX-1) {
         rear = -1;
      }
      intArray[++rear] = data;
      itemCount++;
   }
}
int removeData(){
   int data = intArray[front++];
   if(front == MAX) {
      front = 0;
   }
   itemCount--;
   return data;
}
int main(){
   int i;
   
   /* insert 5 items */
   insert(3);
   insert(5);
   insert(9);
   insert(1);
   insert(12);
   insert(15);
   printf("Queue: ");
   for(i = 0; i < MAX; i++)
      printf("%d ", intArray[i]);

   // remove one item
   int num = removeData();
   printf("\nElement removed: %d\n",num);
   printf("Updated Queue: ");
   while(!isEmpty()) {
      int n = removeData();
      printf("%d ",n);
   }
}

輸出

Queue: 3 5 9 1 12 15 
Element removed: 3
Updated Queue: 5 9 1 12 15 

#include <iostream>
#include <string>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
bool isFull(){
   return itemCount == MAX;
}
bool isEmpty(){
   return itemCount == 0;
}
void insert(int data){
   if(!isFull()) {
      if(rear == MAX-1) {
         rear = -1;
      }
      intArray[++rear] = data;
      itemCount++;
   }
}
int removeData(){
   int data = intArray[front++];
   if(front == MAX) {
      front = 0;
   }
   itemCount--;
   return data;
}
int main(){
   int i;
   
   /* insert 5 items */
   insert(3);
   insert(5);
   insert(9);
   insert(1);
   insert(12);
   insert(15);
   printf("Queue: ");
   for(i = 0; i < MAX; i++)
      printf("%d ", intArray[i]);
   
   // remove one item
   int num = removeData();
   printf("\nElement removed: %d\n",num);
   printf("Updated Queue: ");
   while(!isEmpty()) {
      int n = removeData();
      printf("%d ",n);
   }
}

輸出

Queue: 3 5 9 1 12 15 
Element removed: 3
Updated Queue: 5 9 1 12 15 

public class Demo{
static final int MAX = 6;
static int intArray[] = new int[MAX];
static int front = 0;
static int rear = -1;
static int itemCount = 0;
public static boolean isFull(){
   return itemCount == MAX;
}
public static boolean isEmpty(){
   return itemCount == 0;
}
public static void insert(int data){
   if(!isFull()) {
      if(rear == MAX-1) {
         rear = -1;
      }
      intArray[++rear] = data;
      itemCount++;
   }
}
public static int removeData(){
   int data = intArray[front++];
   if(front == MAX) {
      front = 0;
   }
   itemCount--;
   return data;
}
public static void main(String[] args){
   int i;
   /* insert 5 items */
   insert(3);
   insert(5);
   insert(9);
   insert(1);
   insert(12);
   insert(15);
   System.out.print("Queue: ");
   for(i = 0; i < MAX; i++)
      System.out.print(intArray[i] + " ");
   
   // remove one item
   int num = removeData();
   System.out.print("\nElement removed: " + num);
   System.out.print("\nUpdated Queue: ");
   while(!isEmpty()) {
      int n = removeData();
      System.out.print(n + " ");
   }
  }
}

輸出

Queue: 3 5 9 1 12 15 
Element removed: 3
Updated Queue: 5 9 1 12 15 

MAX = 6
intArray = [0] * MAX
front = 0
rear = -1
itemCount = 0
def isFull():
    return itemCount == MAX
def isEmpty():
    return itemCount == 0
def insert(data):
    global rear, itemCount
    if not isFull():
        if rear == MAX-1:
            rear = -1
        rear += 1
        intArray[rear] = data
        itemCount += 1
def removeData():
    global front, itemCount
    data = intArray[front]
    if front == MAX-1:
        front = 0
    else:
        front += 1
    itemCount -= 1
    return data
insert(3);
insert(5);
insert(9);
insert(1);
insert(12);
insert(15);
print("Queue: ")
for i in range(MAX):
    print(intArray[i], end = " ")
num = removeData()
print("\nElement removed: ", num)
print("Updated Queue: ")
while(not isEmpty()):
    n = removeData()
    print(n, end = " ")

輸出

Queue: 
3 5 9 1 12 15 
Element removed:  3
Updated Queue: 
5 9 1 12 15

佇列 - peek() 操作

peek() 操作用於檢索佇列中最前面的元素，而無需刪除它。此操作用於藉助指標檢查佇列的狀態。

演算法

1. START
2. Return the element at the front of the queue
3. END

示例

以下是此操作在各種程式語言中的實現 -

C C++ Java Python
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
int peek(){
   return intArray[front];
}
bool isFull(){
   return itemCount == MAX;
}
void insert(int data){
   if(!isFull()) {
      if(rear == MAX-1) {
         rear = -1;
      }
      intArray[++rear] = data;
      itemCount++;
   }
}
int main(){
   int i;
   
   /* insert 5 items */
   insert(3);
   insert(5);
   insert(9);
   insert(1);
   insert(12);
   insert(15);
   printf("Queue: ");
   for(i = 0; i < MAX; i++)
      printf("%d ", intArray[i]);
   printf("\nElement at front: %d\n",peek());
}

輸出

Queue: 3 5 9 1 12 15 
Element at front: 3

#include <iostream>
#include <string>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
int peek(){
   return intArray[front];
}
bool isFull(){
   return itemCount == MAX;
}
void insert(int data){
   if(!isFull()) {
      if(rear == MAX-1) {
         rear = -1;
      }
      intArray[++rear] = data;
      itemCount++;
   }
}
int main(){
   int i;
   /* insert 5 items */
   insert(3);
   insert(5);
   insert(9);
   insert(1);
   insert(12);
   insert(15);
   printf("Queue: ");
   for(i = 0; i < MAX; i++)
      printf("%d ", intArray[i]);
   printf("\nElement at front: %d\n",peek());
}

輸出

Queue: 3 5 9 1 12 15 
Element at front: 3

public class Demo{
final static int MAX = 6;
static int intArray[] = new int[MAX];
static int front = 0;
static int rear = -1;
static int itemCount = 0;
public static int peek(){
   return intArray[front];
}
public static boolean isFull(){
   return itemCount == MAX;
}
public static void insert(int data){
   if(!isFull()) {
      if(rear == MAX-1) {
         rear = -1;
      }
      intArray[++rear] = data;
      itemCount++;
   }
}
public static void main(String[] args){
   int i;
   /* insert 5 items */
   insert(3);
   insert(5);
   insert(9);
   insert(1);
   insert(12);
   insert(15);
   System.out.print("Queue: ");
   for(i = 0; i < MAX; i++)
      System.out.print(intArray[i] + " ");
   System.out.print("\nElement at front: " + peek());
  }
}

輸出

Queue: 3 5 9 1 12 15 
Element at front: 3

MAX = 6
intArray = [0] * MAX
front = 0
rear = -1
itemCount = 0
def peek():
    return intArray[front]
def isFull():
    return itemCount == MAX
def insert(data):
    global rear, itemCount
    if(not isFull()):
        if(rear == MAX-1):
            rear = -1
        rear  = rear + 1
        intArray[rear] = data
        itemCount+1
insert(3);
insert(5);
insert(9);
insert(1);
insert(12);
insert(15);
print("Queue: ")
for i in range(MAX):
    print(intArray[i], end = " ")
print("\nElement at front: ", peek())

輸出

Queue: 
3 5 9 1 12 15 
Element at front:  3

佇列 - isFull() 操作

isFull() 操作驗證棧是否已滿。

演算法

1. START
2. If the count of queue elements equals the queue size,
   return true
3. Otherwise, return false
4. END

示例

以下是此操作在各種程式語言中的實現 -

C C++ Java Python
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
bool isFull(){
   return itemCount == MAX;
}
void insert(int data){
   if(!isFull()) {
      if(rear == MAX-1) {
         rear = -1;
      }
      intArray[++rear] = data;
      itemCount++;
   }
}
int main(){
   int i;
   /* insert 5 items */
   insert(3);
   insert(5);
   insert(9);
   insert(1);
   insert(12);
   insert(15);
   printf("Queue: ");
   for(i = 0; i < MAX; i++)
      printf("%d ", intArray[i]);
   printf("\n");
   if(isFull()) {
      printf("Queue is full!\n");
   }
}

輸出

Queue: 3 5 9 1 12 15 
Queue is full!

#include <iostream>
#include <string>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
bool isFull(){
   return itemCount == MAX;
}
void insert(int data){
   if(!isFull()) {
      if(rear == MAX-1) {
         rear = -1;
      }
      intArray[++rear] = data;
      itemCount++;
   }
}
int main(){
   int i;
   
   /* insert 5 items */
   insert(3);
   insert(5);
   insert(9);
   insert(1);
   insert(12);
   insert(15);
   printf("Queue: ");
   for(i = 0; i < MAX; i++)
      printf("%d ", intArray[i]);
   printf("\n");
   if(isFull()) {
      printf("Queue is full!\n");
   }
}

輸出

Queue: 3 5 9 1 12 15 
Queue is full!

import java.io.*;
public class QueueExample {
   static private int intArray[];
   private int front;
   private int rear;
   private int itemCount;
   static private int MAX;
   QueueExample(int size) {
      intArray = new int[size];
      front = 0;
      rear = -1;
      MAX = size;
      itemCount = 0;
   }
   public boolean isFull() {
      return itemCount == MAX;
   }
   public void insert(int key) {
      if(!isFull()) {
         if(rear == MAX-1) {
            rear = -1;
         }
         intArray[++rear] = key;
         itemCount++;
      }
   }
   public static void main (String[] args) {
      QueueExample q = new QueueExample(5);
      q.insert(1); // inserting 1 in the stack
      q.insert(2);
      q.insert(3);
      q.insert(4);
      q.insert(5);
      System.out.print("Queue: ");
      for(int i = 0; i<MAX; i++){
          System.out.print(intArray[i] + " ");
      }
      if(q.isFull()){
	  System.out.print("\nQueue is full!");
   }
  }
}

輸出

Queue: 1 2 3 4 5 
Queue is full!

#python code for isFull in Queue
MAX = 6
intArray = [None] * MAX
front = 0
rear = -1
itemCount = 0

def isFull():
    return itemCount == MAX

def insert(data):
    global rear, itemCount
    if not isFull():
        if rear == MAX-1:
            rear = -1
        rear += 1
        intArray[rear] = data
        itemCount += 1
#inserting 5 items into the Queue
insert(3)
insert(5)
insert(9)
insert(1)
insert(12)
insert(15)
print("Queue: ", end="")
for i in range(MAX):
    print(intArray[i], end=" ")
print()
if isFull():
    print("Queue is full!")

輸出

Queue: 3 5 9 1 12 15 
Queue is full!

佇列 - isEmpty() 操作

isEmpty() 操作驗證棧是否為空。此操作用於藉助 top 指標檢查棧的狀態。

演算法

1. START
2. If the count of queue elements equals zero, return true
3. Otherwise, return false
4. END

示例

以下是此操作在各種程式語言中的實現 -

C C++ Java Python
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
bool isEmpty(){
   return itemCount == 0;
}
int main(){
   int i;
   printf("Queue: ");
   for(i = 0; i < MAX; i++)
      printf("%d ", intArray[i]);
   printf("\n");
   if(isEmpty()) {
      printf("Queue is Empty!\n");
   }
}

輸出

Queue: 0 0 0 0 0 0 
Queue is Empty!

#include <iostream>
#include <string>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
bool isEmpty(){
   return itemCount == 0;
}
int main(){
   int i;
   printf("Queue: ");
   for(i = 0; i < MAX; i++)
      printf("%d ", intArray[i]);
   printf("\n");
   if(isEmpty()) {
      printf("Queue is Empty!\n");
   }
}

輸出

Queue: 0 0 0 0 0 0 
Queue is Empty!

public class Demo{
final static int MAX = 6;
static int intArray[] = new int[MAX];
static int front = 0;
static int rear = -1;
static int itemCount = 0;
public static boolean isEmpty(){
   return itemCount == 0;
}
public static void main(String[] args){
   int i;
   System.out.print("Queue: ");
   for(i = 0; i < MAX; i++)
      System.out.print(intArray[i] + " ");
   if(isEmpty()) {
      System.out.print("\nQueue is Empty!");
   }
 }
}

輸出

Queue: 0 0 0 0 0 0 
Queue is Empty!

#python code for isFull in Queue
MAX = 6
intArray = [None] * MAX
front = 0
rear = -1
itemCount = 0

def isEmpty():
    return itemCount == 0

print("Queue: ", end="")
for i in range(MAX):
    print(intArray[i], end=" ")
print()
if isEmpty():
    print("Queue is empty!")

輸出

Queue: None None None None None None 
Queue is empty!

佇列完整實現

以下是佇列在各種程式語言中的完整實現 -

C C++ Java Python
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
int peek(){
   return intArray[front];
}
bool isEmpty(){
   return itemCount == 0;
}
bool isFull(){
   return itemCount == MAX;
}
int size(){
   return itemCount;
}
void insert(int data){
   if(!isFull()) {
      if(rear == MAX-1) {
         rear = -1;
      }
      intArray[++rear] = data;
      itemCount++;
   }
}
int removeData(){
   int data = intArray[front++];
   if(front == MAX) {
      front = 0;
   }
   itemCount--;
   return data;
}
int main(){
   
   /* insert 5 items */
   insert(3);
   insert(5);
   insert(9);
   insert(1);
   insert(12);
   insert(15);
   printf("Queue size: %d", size());
   printf("\nQueue: ");
   for(int i = 0; i < MAX; i++){
       printf("%d ", intArray[i]);
   }
   if(isFull()) {
      printf("\nQueue is full!");
   }

   // remove one item
   int num = removeData();
   printf("\nElement removed: %d", num);
   printf("\nSize of Queue after deletion: %d", size());
   printf("\nElement at front: %d", peek());
}

輸出

Queue size: 6
Queue: 3 5 9 1 12 15 
Queue is full!
Element removed: 3
Size of Queue after deletion: 5
Element at front: 5

#include <iostream>
using namespace std;
#include <string>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
int peek(){
   return intArray[front];
}
bool isEmpty(){
   return itemCount == 0;
}
bool isFull(){
   return itemCount == MAX;
}
int size(){
   return itemCount;
}
void insert(int data){
   if(!isFull()) {
      if(rear == MAX-1) {
         rear = -1;
      }
      intArray[++rear] = data;
      itemCount++;
   }
}
int removeData(){
   int data = intArray[front++];
   if(front == MAX) {
      front = 0;
   }
   itemCount--;
   return data;
}
int main(){
   
   /* insert 5 items */
   insert(3);
   insert(5);
   insert(9);
   insert(1);
   insert(12);
   insert(15);
   cout<<"Queue size: "<<size();
   cout<<"\nQueue: ";
   for(int i = 0; i < MAX; i++){
       cout<<intArray[i]<<" ";
   }
   if(isFull()) {
      cout<<"\nQueue is full!";
   }

   // remove one item
   int num = removeData();
   cout<<"\nElement removed: "<<num;
   cout<<"\nQueue size after deletion: "<<size();
   cout<<"\nElement at front: " <<peek();
}

輸出

Queue size: 6
Queue: 3 5 9 1 12 15 
Queue is full!
Element removed: 3
Queue size after deletion: 5
Element at front: 5

public class Demo{
final static int MAX = 6;
static int intArray[] = new int[MAX];
static int front = 0;
static int rear = -1;
static int itemCount = 0;
public static int peek(){
   return intArray[front];
}
public static boolean isEmpty(){
   return itemCount == 0;
}
public static boolean isFull(){
   return itemCount == MAX;
}
public static int size(){
   return itemCount;
}
public static void insert(int data){
   if(!isFull()) {
      if(rear == MAX-1) {
         rear = -1;
      }
      intArray[++rear] = data;
      itemCount++;
   }
}
public static int removeData(){
   int data = intArray[front++];
   if(front == MAX) {
      front = 0;
   }
   itemCount--;
   return data;
}
public static void main(String[] args){
   
   /* insert 5 items */
   insert(3);
   insert(5);
   insert(9);
   insert(1);
   insert(12);
   insert(15);
   System.out.print("Queue size: " + size());
   System.out.print("\nQueue: ");
   for(int i = 0; i < MAX; i++){
       System.out.print(intArray[i] + " ");
   }
   if(isFull()) {
      System.out.print("\nQueue is full!");
   }

   // remove one item
   int num = removeData();
   System.out.print("\nElement removed: " + num);
   System.out.print("\nQueue size after deletion: " + size());
   System.out.print("\nElement at front: " + peek());
 }
}

輸出

Queue size: 6
Queue: 3 5 9 1 12 15 
Queue is full!
Element removed: 3
Queue size after deletion: 5
Element at front: 5

MAX = 6
intArray = [0] * MAX
front = 0
rear = -1
itemCount = 0
def peek():
    return intArray[front]

def isEmpty():
    return itemCount == 0

def isFull():
    return itemCount == MAX

def size():
    return itemCount

def insert(data):
    global rear, itemCount
    if not isFull():
        if rear == MAX-1:
            rear = -1
        rear += 1
        intArray[rear] = data
        itemCount += 1

def removeData():
    global front, itemCount
    data = intArray[front]
    if front == MAX-1:
        front = 0
    else:
        front += 1
    itemCount -= 1
    return data

def main():
    insert(3)
    insert(5)
    insert(9)
    insert(1)
    insert(12)
    insert(15)
    print("Queue size: ", size())
    print("Queue: ")
    for i in range(MAX):
        print(intArray[i], end = " ")
    if isFull():
        print("\nQueue is full!")
    num = removeData()
    print("Element removed: ", num)
    print("Queue size after deletion: ", size())
    print("Element at front: ", peek())

main()

輸出

Queue size:  6
Queue: 
3 5 9 1 12 15 
Queue is full!
Element removed:  3
Queue size after deletion:  5
Element at front:  5

C語言中的佇列實現

點選檢視使用C語言編寫的佇列程式的實現

列印頁面
上一頁
下一頁
廣告