插入排序演算法

插入排序是一種非常簡單的方法，用於將數字按升序或降序排序。此方法遵循增量方法。可以將其與玩遊戲時整理撲克牌的技術進行比較。

這是一種基於比較的原地排序演算法。在此，維護一個始終排序的子列表。例如，陣列的下半部分保持排序狀態。要“插入”到此排序子列表中的元素必須找到其適當的位置，然後將其插入到該位置。因此得名：**插入排序**。

順序搜尋陣列並將未排序的專案移動並插入到排序的子列表（在同一個陣列中）。此演算法不適用於大型資料集，因為其平均和最壞情況的複雜度為 Ο(n²)，其中n 是專案的數量。

插入排序演算法

現在我們對這種排序技術的運作方式有了更全面的瞭解，因此我們可以推匯出一些簡單的步驟來實現插入排序。

**步驟 1** - 如果是第一個元素，則已排序。返回 1;

**步驟 2** - 選擇下一個元素

**步驟 3** - 與排序子列表中的所有元素進行比較

**步驟 4** - 將排序子列表中所有大於要排序的值的元素進行移位

**步驟 5** - 插入該值

**步驟 6** - 重複此過程，直到列表排序

虛擬碼

Algorithm: Insertion-Sort(A)
for j = 2 to A.length
   key = A[j]
   i = j – 1
   while i > 0 and A[i] > key
      A[i + 1] = A[i]
      i = i -1
   A[i + 1] = key

分析

此演算法的執行時間很大程度上取決於給定的輸入。

如果給定的數字已排序，則此演算法在O(n)時間內執行。如果給定的數字按相反順序排列，則演算法在O(n²)時間內執行。

示例

我們以一個未排序的陣列為例。

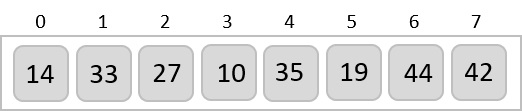
插入排序比較前兩個元素。

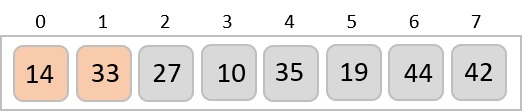
它發現 14 和 33 已經按升序排列。目前，14 位於排序子列表中。

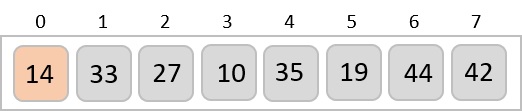
插入排序繼續向前，將 33 與 27 進行比較。

並發現 33 不在正確的位置。它將 33 與 27 交換。它還檢查排序子列表的所有元素。在這裡，我們看到排序子列表只有一個元素 14，而 27 大於 14。因此，交換後排序子列表仍然保持排序狀態。

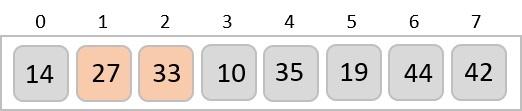
到目前為止，我們在排序子列表中有了 14 和 27。接下來，它將 33 與 10 進行比較。這些值沒有按排序順序排列。

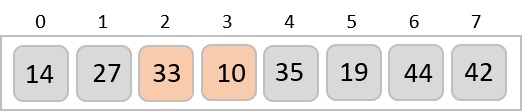
因此它們被交換。

但是，交換導致 27 和 10 未排序。

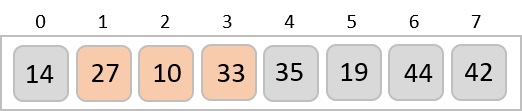
因此，我們也交換它們。

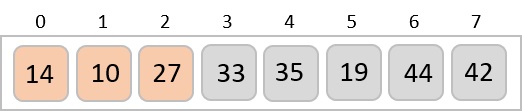
我們再次發現 14 和 10 未排序。

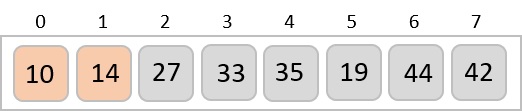
我們再次交換它們。

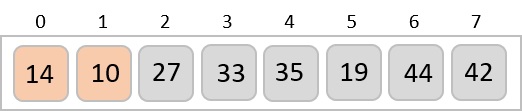
在第三次迭代結束時，我們有一個包含 4 個元素的排序子列表。

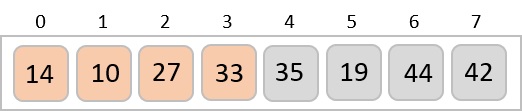
此過程持續進行，直到所有未排序的值都被包含在排序子列表中。現在我們將瞭解插入排序的一些程式設計方面。

實現

由於插入排序是一種原地排序演算法，因此演算法的實現方式是，將迭代選擇為陣列中每個元素的關鍵元素與後續元素進行比較以檢查其位置。如果關鍵元素小於其後續元素，則不進行交換。否則，將交換這兩個比較的元素，並將下一個元素選擇為關鍵元素。

插入排序已在四種程式語言中實現，分別是 C、C++、Java 和 Python -

#include <stdio.h>
void insertionSort(int array[], int size){
   int key, j;
   for(int i = 1; i<size; i++) {
      key = array[i];//take value
      j = i;
      while(j > 0 && array[j-1]>key) {
         array[j] = array[j-1];
         j--;
      }
      array[j] = key; //insert in right place
   }
}
int main(){
   int n;
   n = 5;
   int arr[5] = {67, 44, 82, 17, 20}; // initialize the array
   printf("Array before Sorting: ");
   for(int i = 0; i<n; i++)
      printf("%d ",arr[i]);
   printf("\n");
   insertionSort(arr, n);
   printf("Array after Sorting: ");
   for(int i = 0; i<n; i++)
      printf("%d ", arr[i]);
   printf("\n");
}

Array before Sorting: 67 44 82 17 20 
Array after Sorting: 17 20 44 67 82 

#include<iostream>
using namespace std;
void insertionSort(int *array, int size){
   int key, j;
   for(int i = 1; i<size; i++) {
      key = array[i];//take value
      j = i;
      while(j > 0 && array[j-1]>key) {
         array[j] = array[j-1];
         j--;
      }
      array[j] = key; //insert in right place
   }
}
int main(){
   int n;
   n = 5;
   int arr[5] = {67, 44, 82, 17, 20}; // initialize the array
   cout << "Array before Sorting: ";
   for(int i = 0; i<n; i++)
      cout << arr[i] << " ";
   cout << endl;
   insertionSort(arr, n);
   cout << "Array after Sorting: ";
   for(int i = 0; i<n; i++)
      cout << arr[i] << " ";
   cout << endl;
}

Array before Sorting: 67 44 82 17 20
Array after Sorting: 17 20 44 67 82

import java.io.*;
public class InsertionSort {
   public static void main(String args[]) {
      int n = 5;
      int[] arr = {67, 44, 82, 17, 20}; //initialize an array
      System.out.print("Array before Sorting: ");
      for(int i = 0; i<n; i++)
         System.out.print(arr[i] + " ");
      System.out.println();
      for(int i = 1; i<n; i++) {
         int key = arr[i];//take value
         int j = i;
         while(j > 0 && arr[j-1]>key) {
            arr[j] = arr[j-1];
            j--;
         }
         arr[j] = key; //insert in right place
      }
      System.out.print("Array After Sorting: ");
      for(int i = 0; i<n; i++)
         System.out.print(arr[i] + " ");
      System.out.println();
   }
}

Array before Sorting: 67 44 82 17 20
Array After Sorting: 17 20 44 67 82

def insertion_sort(array, size):
   for i in range(1, size):
      key = array[i]
      j = i
      while (j > 0) and (array[j-1] > key):
         array[j] = array[j-1]
         j = j-1
      array[j] = key
      
arr = [67, 44, 82, 17, 20]
n = len(arr)
print("Array before Sorting: ")
print(arr)
insertion_sort(arr, n);
print("Array after Sorting: ")
print(arr)

Array before Sorting: 
[67, 44, 82, 17, 20]
Array after Sorting: 
[17, 20, 44, 67, 82]