隨機快速排序演算法

Table of content
上一頁
下一頁

快速排序是一種流行的排序演算法，它選擇一個樞紐元素，並圍繞該樞紐元素對輸入列表進行排序。要了解有關快速排序的更多資訊，請點選此處。

隨機快速排序旨在降低演算法以最壞情況時間複雜度O(n2)執行的可能性。快速排序的最壞情況時間複雜度出現在輸入為已排序列表時，導致n(n – 1)次比較。隨機化快速排序有兩種方法：

  • 隨機打亂輸入：對輸入列表進行隨機化，以便再次打亂已排序的輸入，從而降低時間複雜度。但是，這通常不會在隨機快速排序中執行。

  • 隨機選擇樞紐元素：使樞紐元素成為隨機變數是隨機快速排序中常用的方法。在這裡，即使輸入已排序，樞紐元素也是隨機選擇的，因此避免了最壞情況的時間複雜度。

隨機快速排序演算法

該演算法完全遵循標準演算法，只是將樞紐選擇隨機化。

虛擬碼

partition-left(arr[], low, high)
   pivot = arr[high]
   i = low // place for swapping
   for j := low to high – 1 do
      if arr[j] <= pivot then
         swap arr[i] with arr[j]
         i = i + 1
   swap arr[i] with arr[high]
   return i

partition-right(arr[], low, high)
   r = Random Number from low to high
   Swap arr[r] and arr[high]
   return partition-left(arr, low, high)

quicksort(arr[], low, high)
   if low < high
      p = partition-right(arr, low, high)
      quicksort(arr, low , p-1)
      quicksort(arr, p+1, high)

示例

讓我們來看一個例子，以瞭解隨機快速排序如何在避免最壞情況時間複雜度方面發揮作用。由於我們正在設計隨機演算法以降低時間複雜度中最壞情況的發生率，因此讓我們以已排序列表作為此示例的輸入。

已排序的輸入列表為3、5、7、8、12、15。我們需要應用快速排序演算法對列表進行排序。

sorted_input_list

步驟1

考慮到可能的最壞情況，如果隨機選擇的樞紐元素也是最高索引數字，它會比較所有其他數字，並選擇另一個樞紐元素。

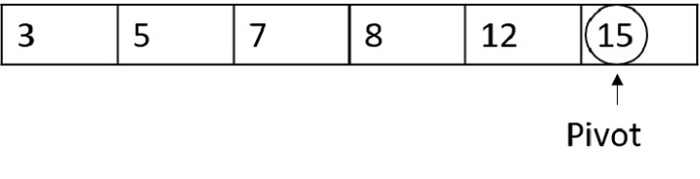
pivot

由於15大於列表中的所有其他數字，因此不會交換，並且會選擇另一個樞紐元素。

步驟2

這次，如果隨機樞紐函式選擇7作為樞紐數字：

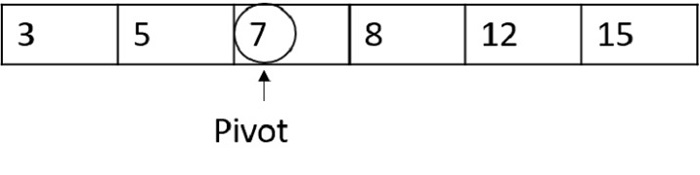
pivot_7

現在，樞紐將列表分成兩半，因此通常執行標準快速排序。但是，時間複雜度比最壞情況低。

需要注意的是，快速排序的最壞情況時間複雜度將始終保持O(n2)，但透過隨機化，我們降低了該最壞情況的發生率。

實施

以下是上述方法在各種程式語言中的實現：

C C++ Java Python
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
// Function to swap two elements
void swap(int* a, int* b) {
    int t = *a;
    *a = *b;
    *b = t;
}
// Function to partition the array
int partition_left(int arr[], int low, int high) {
    int pivot = arr[high];
    int i = low;
    for (int j = low; j < high; j++) {
        if (arr[j] <= pivot) {
            swap(&arr[i], &arr[j]);
            i++;
        }
    }
    swap(&arr[i], &arr[high]);
    return i;
}
// Function to perform random partition
int partition_right(int arr[], int low, int high) {
    srand(time(NULL));
    int r = low + rand() % (high - low);
    swap(&arr[r], &arr[high]);
    return partition_left(arr, low, high);
}
// Recursive function for quicksort
void quicksort(int arr[], int low, int high) {
    if (low < high) {
        int p = partition_right(arr, low, high);
        quicksort(arr, low, p - 1);
        quicksort(arr, p + 1, high);
    }
}
// Function to print the array
void printArray(int arr[], int size) {
    for (int i = 0; i < size; i++)
        printf("%d ", arr[i]);
    printf("\n");
}
// Driver code
int main() {
    int arr[] = { 6, 4, 12, 8, 15, 16};
    int n = sizeof(arr) / sizeof(arr[0]);
    printf("Original array: ");
    printArray(arr, n);
    quicksort(arr, 0, n - 1);
    printf("Sorted array: ");
    printArray(arr, n);
    return 0;
}

輸出

Original array: 6 4 12 8 15 16 
Sorted array: 4 6 8 12 15 16

#include <iostream>
#include <cstdlib>
#include <ctime>
// Function to swap two elements
void swap(int arr[], int i, int j) {
    int temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}
// Function to partition the array
int partitionLeft(int arr[], int low, int high) {
    int pivot = arr[high];
    int i = low;
    for (int j = low; j < high; j++) {
        if (arr[j] <= pivot) {
            swap(arr, i, j);
            i++;
        }
    }
    swap(arr, i, high);
    return i;
}
// Function to perform random partition
int partitionRight(int arr[], int low, int high) {
    srand(time(NULL));
    int r = low + rand() % (high - low);
    swap(arr, r, high);
    return partitionLeft(arr, low, high);
}
// Recursive function for quicksort
void quicksort(int arr[], int low, int high) {
    if (low < high) {
        int p = partitionRight(arr, low, high);
        quicksort(arr, low, p - 1);
        quicksort(arr, p + 1, high);
    }
}
// Function to print the array
void printArray(int arr[], int size) {
    for (int i = 0; i < size; i++)
        std::cout << arr[i] << " ";
    std::cout << std::endl;
}
// Driver code
int main() {
    int arr[] = {6, 4, 12, 8, 15, 16};
    int n = sizeof(arr) / sizeof(arr[0]);
    std::cout << "Original array: ";
    printArray(arr, n);
    quicksort(arr, 0, n - 1);
    std::cout << "Sorted array: ";
    printArray(arr, n);
    return 0;
}

輸出

Original array: 6 4 12 8 15 16 
Sorted array: 4 6 8 12 15 16 

import java.util.Arrays;
import java.util.Random;
public class QuickSort {
    // Function to swap two elements
    static void swap(int[] arr, int i, int j) {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }
    // Function to partition the array
    static int partitionLeft(int[] arr, int low, int high) {
        int pivot = arr[high];
        int i = low;
        for (int j = low; j < high; j++) {
            if (arr[j] <= pivot) {
                swap(arr, i, j);
                i++;
            }
        }
        swap(arr, i, high);
        return i;
    }
    // Function to perform random partition
    static int partitionRight(int[] arr, int low, int high) {
        Random rand = new Random();
        int r = low + rand.nextInt(high - low);
        swap(arr, r, high);
        return partitionLeft(arr, low, high);
    }
    // Recursive function for quicksort
    static void quicksort(int[] arr, int low, int high) {
        if (low < high) {
            int p = partitionRight(arr, low, high);
            quicksort(arr, low, p - 1);
            quicksort(arr, p + 1, high);
        }
    }
    // Function to print the array
    static void printArray(int[] arr) {
        for (int element : arr) {
            System.out.print(element + " ");
        }
        System.out.println();
    }
    // Driver code
    public static void main(String[] args) {
        int[] arr = {6, 4, 12, 8, 15, 16};
        int n = arr.length;
        System.out.print("Original array: ");
        printArray(arr);
        quicksort(arr, 0, n - 1);
        System.out.print("Sorted array: ");
        printArray(arr);
    }
}

輸出

Original array: 6 4 12 8 15 16 
Sorted array: 4 6 8 12 15 16 

import random
# Function to partition the array
def partition_left(arr, low, high):
    pivot = arr[high]
    i = low
    for j in range(low, high):
        if arr[j] <= pivot:
            arr[i], arr[j] = arr[j], arr[i]
            i += 1
    arr[i], arr[high] = arr[high], arr[i]
    return i
# Function to perform random partition
def partition_right(arr, low, high):
    r = random.randint(low, high)
    arr[r], arr[high] = arr[high], arr[r]
    return partition_left(arr, low, high)
# Recursive function for quicksort
def quicksort(arr, low, high):
    if low < high:
        p = partition_right(arr, low, high)
        quicksort(arr, low, p - 1)
        quicksort(arr, p + 1, high)
# Function to print the array
def printArray(arr):
    for element in arr:
        print(element, end=" ")
    print()
# Driver code
arr = [6, 4, 12, 8, 15, 16]
n = len(arr)
print("Original array:", end=" ")
printArray(arr)
quicksort(arr, 0, n - 1)
print("Sorted array:", end=" ")
printArray(arr)

輸出

Original array: 6 4 12 8 15 16 
Sorted array: 4 6 8 12 15 16
列印頁面
上一頁
下一頁
廣告