遞迴演算法

遞迴

許多計算機程式語言允許模組或函式呼叫自身。這種技術稱為遞迴。在遞迴中，函式α要麼直接呼叫自身，要麼呼叫一個函式β，而該函式又反過來呼叫原始函式α。函式α稱為遞迴函式。

示例 - 函式呼叫自身。

int function(int value) {
   if(value < 1)
      return;
   function(value - 1);

   printf("%d ",value);   
}

示例 - 一個函式呼叫另一個函式，而另一個函式又反過來呼叫它。

int function1(int value1) {
   if(value1 < 1)
      return;
   function2(value1 - 1);
   printf("%d ",value1);   
}
int function2(int value2) {
   function1(value2);
}

屬性

遞迴函式可能像迴圈一樣無限執行。為了避免遞迴函式無限執行，遞迴函式必須具有兩個屬性：

• 基本條件 - 必須至少有一個基本條件，當滿足此條件時，函式停止遞迴呼叫自身。

• 漸進式方法 - 遞迴呼叫應該以這樣的方式進行，每次進行遞迴呼叫時都更接近基本條件。

實現

許多程式語言透過棧來實現遞迴。通常，每當一個函式（呼叫者）呼叫另一個函式（被呼叫者）或自身作為被呼叫者時，呼叫者函式將執行控制轉移給被呼叫者。此轉移過程可能還涉及一些資料從呼叫者傳遞給被呼叫者。

這意味著呼叫者函式必須暫時暫停其執行，並在執行控制從被呼叫者函式返回時恢復。在這裡，呼叫者函式需要從其暫停執行的點開始精確地執行。它還需要它正在處理的完全相同的資料值。為此，將為呼叫者函式建立一個啟用記錄（或堆疊幀）。

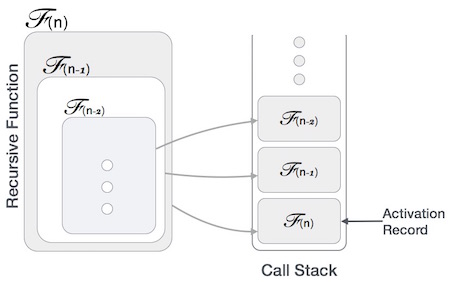
此啟用記錄儲存有關區域性變數、形式引數、返回地址以及傳遞給呼叫者函式的所有資訊。

遞迴分析

有人可能會質疑為什麼要使用遞迴，因為可以使用迭代來完成相同的任務。第一個原因是，遞迴使程式更易於閱讀，並且由於最新的增強型CPU系統，遞迴比迭代更有效。

時間複雜度

對於迭代，我們採用迭代次數來計算時間複雜度。同樣，對於遞迴，假設一切都是常數，我們試圖找出遞迴呼叫的次數。對函式的呼叫為O(1)，因此遞迴呼叫n次使得遞迴函式為O(n)。

空間複雜度

空間複雜度計算的是模組執行需要多少額外空間。對於迭代，編譯器幾乎不需要任何額外空間。編譯器不斷更新迭代中使用的變數的值。但是對於遞迴，系統需要在每次進行遞迴呼叫時儲存啟用記錄。因此，認為遞迴函式的空間複雜度可能高於具有迭代的函式。

示例

以下是各種程式語言中遞迴的實現：

// C program for Recursion Data Structure
#include <stdio.h>
int factorial(int n) {
    // Base case: factorial of 0 is 1
    if (n == 0)
        return 1;
    // Recursive case: multiply n with factorial of (n-1)
    return n * factorial(n - 1);
}
int main() {
    // case 1
    int number = 6;
    printf("Number is: %d\n" , 6);
    //case 2
    if (number < 0) {
        printf("Error: Factorial is undefined for negative numbers.\n");
        return 1;
    } 
    int result = factorial(number);
    //print the output
    printf("Factorial of %d is: %d\n", number, result);
    return 0;
}

Number is: 6
Factorial of 6 is: 720

// CPP program for Recursion Data Structure
#include <iostream>
int factorial(int n) {
    // Base case: factorial of 0 is 1
    if (n == 0)
        return 1;  
    // Recursive case: multiply n with factorial of (n-1)
    return n * factorial(n - 1);
}
int main() {
    // case 1
    int number = 6;
    std::cout<<"Number is: "<<number<<"\n";
    //case 2
    if (number < 0) {
        std::cout << "Error: Factorial is undefined for negative numbers.\n";
        return 1;
    }
    int result = factorial(number);
    //print the output
    std::cout << "Factorial of " << number << " is: " << result << std::endl;  
    return 0;
}

Number is:  6
Factorial of 6 is: 720

// Java program for Recursion Data Structure
import java.util.Scanner;
public class Main {
    public static int factorial(int n) {
        // Base case: factorial of 0 is 1
        if (n == 0)
            return 1;
        // Recursive case: multiply n with factorial of (n-1)
        return n * factorial(n - 1);
    }
    public static void main(String[] args) {
        //Case 1
        int number = 6;
		System.out.println("Number is: " + number);
        //Case 2
        if (number < 0) {
            System.out.println("Error: Factorial is undefined for negative numbers.");
            System.exit(1);
        }
        int result = factorial(number);
        //print the output
        System.out.println("Factorial of " + number + " is: " + result);
    }
}

Number is: 6
Factorial of 6 is: 720

# Python program for Recursion Data Structure
def factorial(n):
    #Base Case: factorial of 0 is 1
    if n == 0:
        return 1
    # Recursive case: multiply n with factorial of (n-1)
    return n * factorial(n - 1)
#Case 1:
number = 6;
print("Number is: ", number);
#Case 2:
if number < 0:
    print("Error: Factorial is undefined for negative numbers.")
else:
    result = factorial(number)
    # print the output
    print("Factorial of", number, "is: ", result)

Number is:  6
Factorial of 6 is: 720