分治演算法

Table of content

使用分治法，手頭的問題被分解成更小的子問題，然後每個子問題獨立解決。當我們繼續將子問題分解成更小的子問題時，我們最終可能會到達一個無法再進行分解的階段。這些最小的子問題使用原始解法進行解決，因為計算它們需要較少的時間。最後，將所有子問題的解合併起來，以獲得原始問題的解。

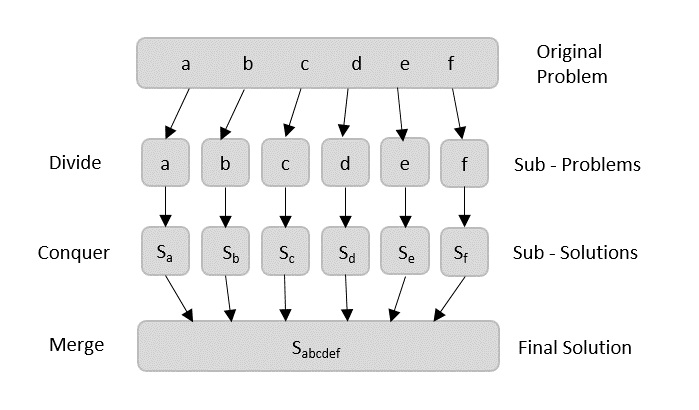
從廣義上講，我們可以將分治方法理解為一個三步過程。

此步驟涉及將問題分解成更小的子問題。子問題應代表原始問題的一部分。此步驟通常採用遞迴方法來劃分問題，直到沒有子問題可以進一步劃分。在此階段，子問題的大小變為原子級別，但仍然代表實際問題的一部分。

此步驟接收許多需要解決的較小子問題。通常，在此級別，問題被認為是“自行解決”的。

當較小的子問題得到解決時，此階段遞迴地將它們組合起來，直到它們形成原始問題的解決方案。這種演算法方法以遞迴方式工作，並且解決和合並步驟非常接近，以至於它們看起來像一個步驟。

陣列作為輸入

各種演算法可以以各種方式接收輸入，以便可以使用分治技術解決它們。陣列就是其中之一。在需要列表形式輸入的演算法中，例如各種排序演算法，陣列資料結構最常使用。

在下面的排序演算法的輸入中，陣列輸入被分解成子問題，直到它們無法進一步分解。

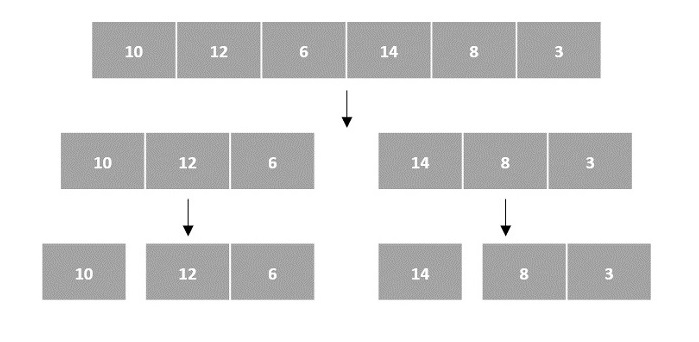
然後，子問題被排序（解決步驟）併合並以形成原始陣列的解決方案（合併步驟）。

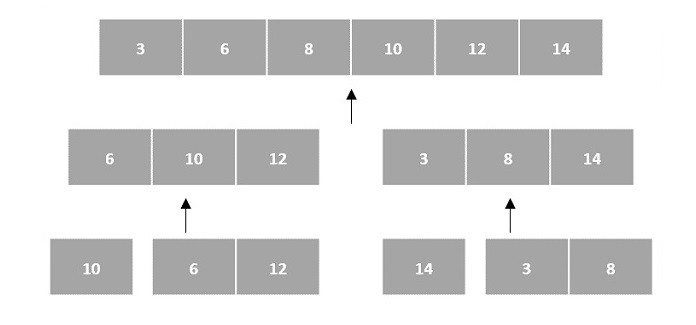
由於陣列是索引的線性資料結構，因此排序演算法最常使用陣列資料結構來接收輸入。

另一種可用於接收分治演算法輸入的資料結構是連結串列（例如，使用連結串列進行歸併排序）。與陣列類似，連結串列也是線性資料結構，按順序儲存資料。

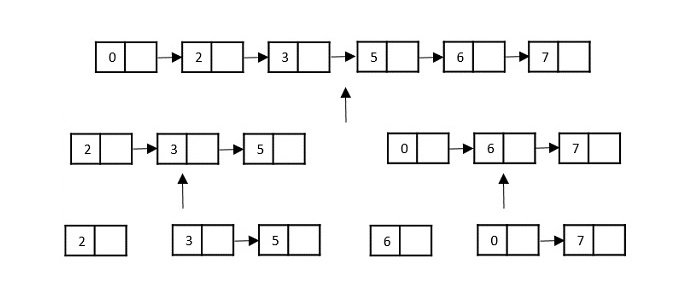
考慮連結串列上的歸併排序演算法；遵循非常流行的龜兔演算法，列表被分割，直到它無法進一步分割。

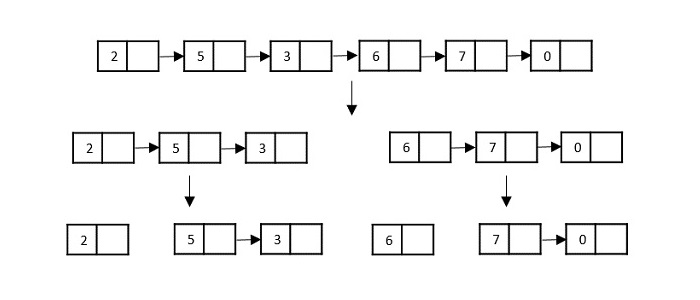
然後，對列表中的節點進行排序（解決）。然後遞迴地組合（或合併）這些節點，直到達到最終解決方案。

各種搜尋演算法也可以在連結串列資料結構上執行，但使用略有不同的技術，因為連結串列不是索引的線性資料結構。必須使用列表節點中可用的指標來處理它們。

分治法支援並行性，因為子問題是獨立的。因此，使用此技術設計的演算法可以在多處理器系統或不同的機器上同時執行。

在這種方法中，大多數演算法都是使用遞迴設計的，因此記憶體管理非常高。對於遞迴函式，使用堆疊，其中需要儲存函式狀態。

以下計算機演算法基於分治程式設計方法 -

有各種方法可以解決任何計算機問題，但上面提到的方法是分治法的很好的例子。

列印頁面