紅黑樹

Table of content
上一頁
下一頁

紅黑樹是另一種平衡二叉搜尋樹，具有兩種顏色的節點：紅色和黑色。它是一種自平衡二叉搜尋樹，利用這些顏色在插入和刪除操作期間保持平衡因子。因此，在紅黑樹操作期間，記憶體使用1位儲存來容納每個節點的顏色資訊。

在紅黑樹（也稱為RB樹）中，為節點分配顏色時需要遵循不同的條件。

  • 根節點始終為黑色。

  • 不允許出現兩個相鄰的紅色節點。

  • 樹中的每條路徑（從根節點到葉節點）必須具有相同數量的黑色節點。

儘管AVL樹比RB樹更平衡，AVL樹的平衡演算法比RB樹更嚴格，但透過RB樹可以使多個和更快的插入和刪除操作更高效。

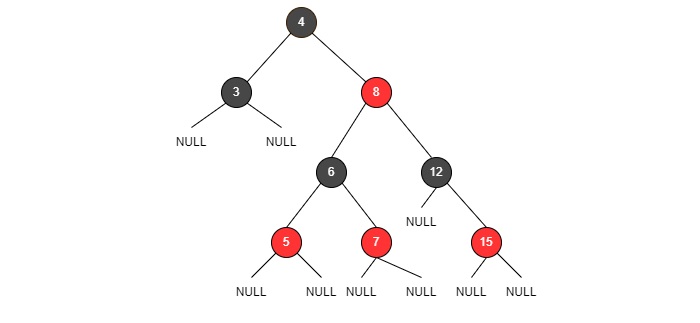
RB trees

圖：RB樹

紅黑樹的基本操作

紅黑樹的操作包括通常在二叉搜尋樹上執行的所有基本操作。RB樹的一些基本操作包括：

  • 插入

  • 刪除

  • 搜尋

插入操作

紅黑樹的插入操作遵循二叉搜尋樹相同的插入演算法。元素按照二叉搜尋屬性插入，此外，節點被著色為紅色和黑色以根據紅黑樹屬性平衡樹。

按照以下步驟，透過保持二叉搜尋樹和紅黑樹屬性來將元素插入紅黑樹。

情況1 - 檢查樹是否為空；如果為空，則將當前節點設為根節點並將其顏色設定為黑色。

情況2 - 但如果樹不為空，我們建立一個新節點並將其顏色設定為紅色。這裡我們面臨兩種不同的情況：

  • 如果新節點的父節點是黑色，則我們退出操作，樹保持不變。

  • 如果新節點的父節點是紅色，並且父節點的兄弟節點的顏色是黑色或不存在，則我們應用適當的旋轉並相應地重新著色。

  • 如果新節點的父節點是紅色，並且父節點的兄弟節點是紅色，則將父節點、兄弟節點和祖父節點重新著色為黑色。只有當祖父節點不是根節點時才重新著色祖父節點；如果它是根節點，則只重新著色父節點和兄弟節點。

示例

讓我們為前7個整數構造一個RB樹，以便詳細瞭解插入操作：

檢查樹為空，因此新增的第一個節點是根節點，顏色為黑色。

first node

現在，樹不為空，因此我們建立一個新節點並新增下一個整數，顏色為紅色。

new node

節點不違反二叉搜尋樹和RB樹屬性，因此我們繼續新增另一個節點。

樹不為空；我們建立一個新的紅色節點，並將下一個整數新增到其中。但是新節點的父節點不是黑色。

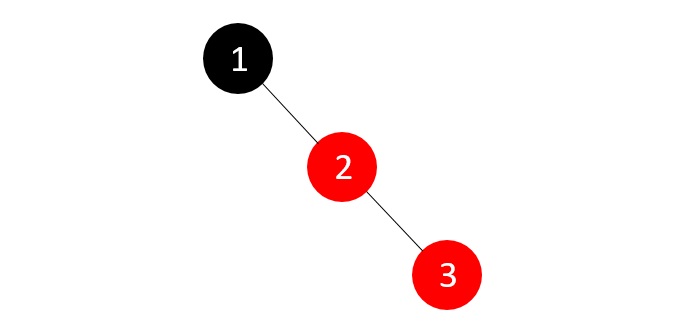
third node

目前的樹違反了二叉搜尋樹和RB樹屬性；由於父節點的兄弟節點為NULL，我們應用適當的旋轉並重新著色節點。

suitable rotation

現在RB樹屬性已恢復，我們向樹中新增另一個節點：

RB Tree property

樹再次違反了RB樹的平衡屬性，因此我們檢查父節點的兄弟節點顏色，在本例中為紅色，因此我們只需重新著色父節點和兄弟節點。

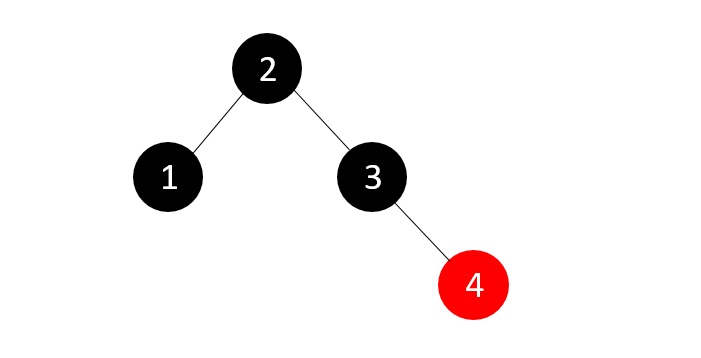
RB Tree balance property

接下來我們插入元素5，這使得樹再次違反RB樹的平衡屬性。

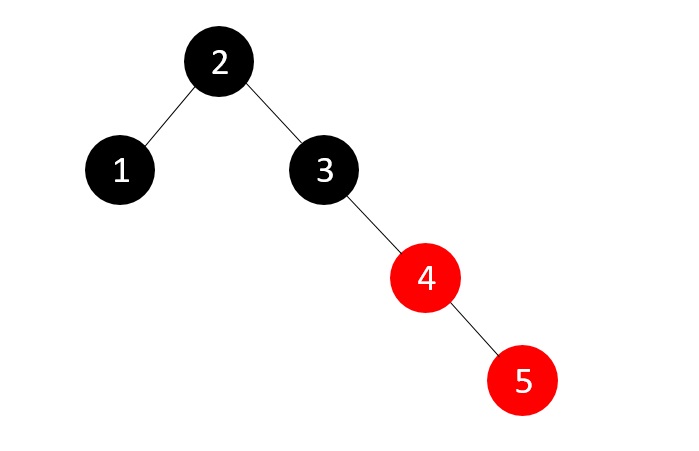
insert element 5

由於兄弟節點為NULL，我們應用適當的旋轉和重新著色。

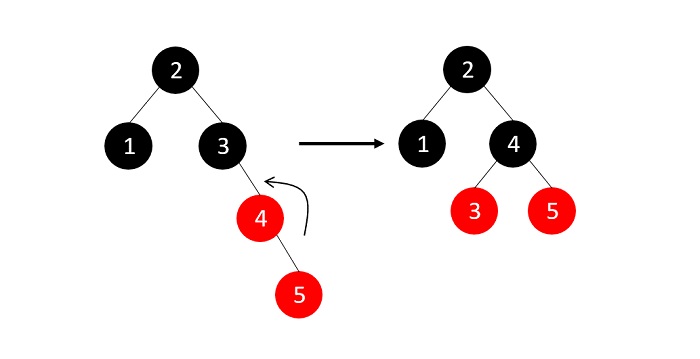
sibling is NULL

現在，我們插入元素6，但是RB樹屬性被違反，需要應用一個插入情況：

insert element 6

父節點的兄弟節點是紅色，因此我們重新著色父節點、父節點的兄弟節點和祖父節點，因為祖父節點不是根節點。

recolor parent

現在，我們新增最後一個元素7，但新節點的父節點是紅色。

add last element

由於父節點的兄弟節點為NULL，我們應用適當的旋轉（RR旋轉）

RB Tree achieved

最終得到RB樹。

刪除操作

紅黑樹的刪除操作必須以這樣一種方式執行：它必須恢復二叉搜尋樹和紅黑樹的所有屬性。按照以下步驟在紅黑樹上執行刪除操作：

首先，我們根據二叉搜尋樹屬性執行刪除。

情況1 - 如果要刪除的節點或節點的父節點是紅色，則只需刪除它。

情況2 - 如果節點是雙黑，則只需刪除雙黑（當要刪除的節點是黑色葉節點時，就會出現雙黑，因為它還會累加被認為是黑色的NULL節點）。

情況3 - 如果雙黑節點的兄弟節點也是黑色節點，並且其子節點也是黑色，則執行以下步驟：

  • 刪除雙黑

  • 將其父節點重新著色為黑色（如果父節點是紅色，則變為黑色；如果父節點已經是黑色，則變為雙黑）

  • 將父節點的兄弟節點重新著色為紅色

  • 如果仍然存在雙黑節點，我們應用其他情況。

情況4 - 如果雙黑節點的兄弟節點是紅色，我們執行以下步驟：

  • 交換父節點和父節點的兄弟節點的顏色。

  • 朝雙黑節點的方向旋轉父節點

  • 重新應用其他適用情況。

情況5 - 如果雙黑節點的兄弟節點是黑色節點，但最靠近雙黑的兄弟節點的子節點是紅色，則執行以下步驟：

  • 交換雙黑節點的兄弟節點和相關兄弟節點子節點的顏色

  • 朝與雙黑節點相反的方向旋轉兄弟節點（即，如果雙黑節點是右子節點，則應用左旋轉，反之亦然）

  • 應用情況6。

情況6 - 如果雙黑節點的兄弟節點是黑色節點，但離雙黑節點較遠的兄弟節點的子節點是紅色，則執行以下步驟：

  • 交換雙黑節點的父節點和兄弟節點的顏色

  • 朝雙黑節點的方向旋轉父節點（即，如果雙黑節點是右子節點，則應用右旋轉，反之亦然）

  • 刪除雙黑

  • 將紅色子節點的顏色更改為黑色。

示例

考慮上面構造的相同的紅黑樹，讓我們從樹中刪除一些元素。

RB Tree achieved

從樹中刪除元素4、5、3。

要刪除元素4，讓我們首先執行二叉搜尋刪除。

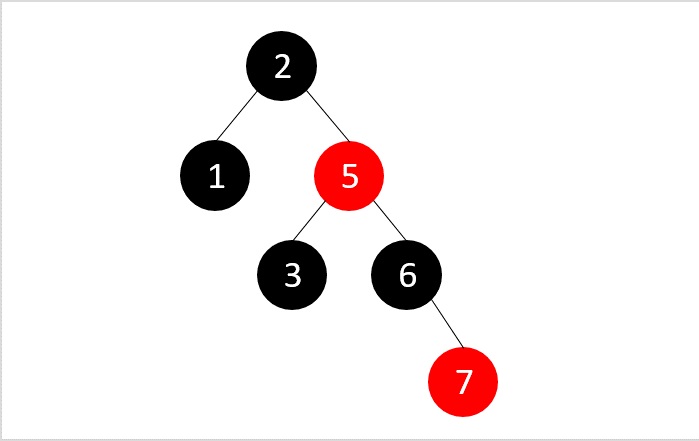
delete element 4

執行二叉搜尋刪除後，RB樹屬性沒有被破壞，因此樹保持不變。

然後，我們使用二叉搜尋刪除來刪除元素5

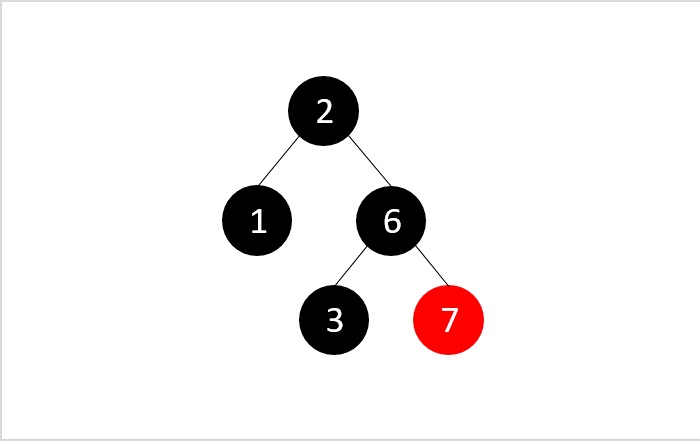
delete element 5

但是執行二叉搜尋刪除後，RB屬性被破壞，即樹中所有路徑不包含相同數量的黑色節點；因此，我們交換顏色以平衡樹。

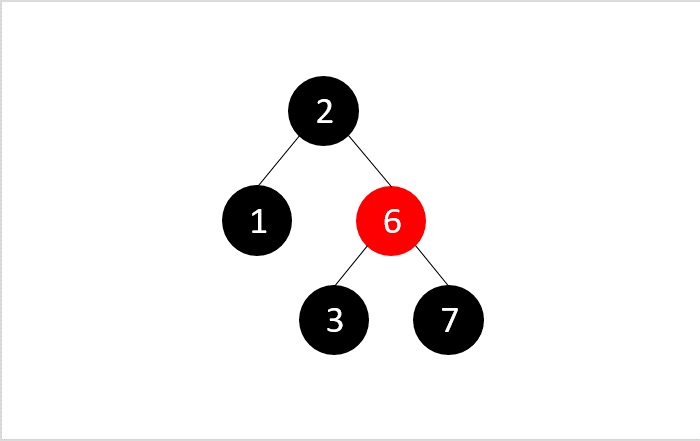
RB property violated

然後，我們從獲得的樹中刪除節點3：

應用二叉搜尋刪除，我們正常刪除節點3，因為它是一個葉節點。並且我們得到一個雙節點，因為3是一個黑色節點。

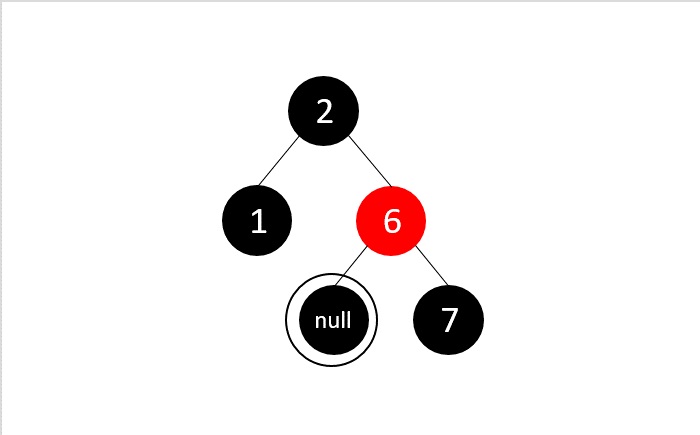
delete node 3

我們應用情況3刪除，因為雙黑節點的兄弟節點是黑色，其子節點也是黑色。在這裡，我們刪除雙黑，重新著色雙黑節點的父節點和兄弟節點。

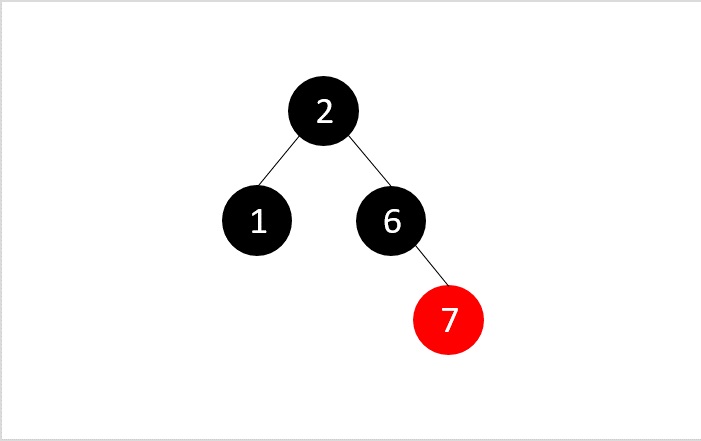
RB Tree property maintained

所有所需節點都被刪除，並且保持了RB樹屬性。

紅黑樹的搜尋操作與二叉搜尋樹的演算法相同。它遍歷樹，並將每個節點與要搜尋的關鍵元素進行比較；如果找到，則返回成功搜尋；否則，返回不成功搜尋。

完整實現

以下是各種程式語言中紅黑樹的完整實現：

C++ Java Python
// C++ program for Red black trees algorithmn
#include <iostream>
using namespace std;
struct Node {
  int data;
  Node *parent;
  Node *left;
  Node *right;
  int color;
};
typedef Node *NodePtr;
class RedBlackTree {
   private:
  NodePtr root;
  NodePtr TNULL;
  void initializeNULLNode(NodePtr node, NodePtr parent) {
    node->data = 0;
    node->parent = parent;
    node->left = nullptr;
    node->right = nullptr;
    node->color = 0;
  }
  // Preorder
  void preOrderHelper(NodePtr node) {
    if (node != TNULL) {
      cout << node->data << " ";
      preOrderHelper(node->left);
      preOrderHelper(node->right);
    }
  }
  // Inorder
  void inOrderHelper(NodePtr node) {
    if (node != TNULL) {
      inOrderHelper(node->left);
      cout << node->data << " ";
      inOrderHelper(node->right);
    }
  }
  // Post order
  void postOrderHelper(NodePtr node) {
    if (node != TNULL) {
      postOrderHelper(node->left);
      postOrderHelper(node->right);
      cout << node->data << " ";
    }
  }
  NodePtr searchTreeHelper(NodePtr node, int key) {
    if (node == TNULL || key == node->data) {
      return node;
    }
    if (key < node->data) {
      return searchTreeHelper(node->left, key);
    }
    return searchTreeHelper(node->right, key);
  }
  // For balancing the tree after deletion
  void deleteFix(NodePtr x) {
    NodePtr s;
    while (x != root && x->color == 0) {
      if (x == x->parent->left) {
        s = x->parent->right;
        if (s->color == 1) {
          s->color = 0;
          x->parent->color = 1;
          leftRotate(x->parent);
          s = x->parent->right;
        }
        if (s->left->color == 0 && s->right->color == 0) {
          s->color = 1;
          x = x->parent;
        } else {
          if (s->right->color == 0) {
            s->left->color = 0;
            s->color = 1;
            rightRotate(s);
            s = x->parent->right;
          }
          s->color = x->parent->color;
          x->parent->color = 0;
          s->right->color = 0;
          leftRotate(x->parent);
          x = root;
        }
      } else {
        s = x->parent->left;
        if (s->color == 1) {
          s->color = 0;
          x->parent->color = 1;
          rightRotate(x->parent);
          s = x->parent->left;
        }
        if (s->right->color == 0 && s->right->color == 0) {
          s->color = 1;
          x = x->parent;
        } else {
          if (s->left->color == 0) {
            s->right->color = 0;
            s->color = 1;
            leftRotate(s);
            s = x->parent->left;
          }
          s->color = x->parent->color;
          x->parent->color = 0;
          s->left->color = 0;
          rightRotate(x->parent);
          x = root;
        }
      }
    }
    x->color = 0;
  }
  void rbTransplant(NodePtr u, NodePtr v) {
    if (u->parent == nullptr) {
      root = v;
    } else if (u == u->parent->left) {
      u->parent->left = v;
    } else {
      u->parent->right = v;
    }
    v->parent = u->parent;
  }
  void deleteNodeHelper(NodePtr node, int key) {
    NodePtr z = TNULL;
    NodePtr x, y;
    while (node != TNULL) {
      if (node->data == key) {
        z = node;
      }
      if (node->data <= key) {
        node = node->right;
      } else {
        node = node->left;
      }
    }
    if (z == TNULL) {
      cout << "Key not found in the tree" << endl;
      return;
    }
    y = z;
    int y_original_color = y->color;
    if (z->left == TNULL) {
      x = z->right;
      rbTransplant(z, z->right);
    } else if (z->right == TNULL) {
      x = z->left;
      rbTransplant(z, z->left);
    } else {
      y = minimum(z->right);
      y_original_color = y->color;
      x = y->right;
      if (y->parent == z) {
        x->parent = y;
      } else {
        rbTransplant(y, y->right);
        y->right = z->right;
        y->right->parent = y;
      }
      rbTransplant(z, y);
      y->left = z->left;
      y->left->parent = y;
      y->color = z->color;
    }
    delete z;
    if (y_original_color == 0) {
      deleteFix(x);
    }
  }
  // For balancing the tree after insertion
  void insertFix(NodePtr k) {
    NodePtr u;
    while (k->parent->color == 1) {
      if (k->parent == k->parent->parent->right) {
        u = k->parent->parent->left;
        if (u->color == 1) {
          u->color = 0;
          k->parent->color = 0;
          k->parent->parent->color = 1;
          k = k->parent->parent;
        } else {
          if (k == k->parent->left) {
            k = k->parent;
            rightRotate(k);
          }
          k->parent->color = 0;
          k->parent->parent->color = 1;
          leftRotate(k->parent->parent);
        }
      } else {
        u = k->parent->parent->right;
        if (u->color == 1) {
          u->color = 0;
          k->parent->color = 0;
          k->parent->parent->color = 1;
          k = k->parent->parent;
        } else {
          if (k == k->parent->right) {
            k = k->parent;
            leftRotate(k);
          }
          k->parent->color = 0;
          k->parent->parent->color = 1;
          rightRotate(k->parent->parent);
        }
      }
      if (k == root) {
        break;
      }
    }
    root->color = 0;
  }
  void printHelper(NodePtr root, string indent, bool last) {
    if (root != TNULL) {
      cout << indent;
      if (last) {
        cout << "R----";
        indent += "   ";
      } else {
        cout << "L----";
        indent += "|  ";
      }
      string sColor = root->color ? "RED" : "BLACK";
      cout << root->data << "(" << sColor << ")" << endl;
      printHelper(root->left, indent, false);
      printHelper(root->right, indent, true);
    }
  }
   public:
  RedBlackTree() {
    TNULL = new Node;
    TNULL->color = 0;
    TNULL->left = nullptr;
    TNULL->right = nullptr;
    root = TNULL;
  }
  void preorder() {
    preOrderHelper(this->root);
  }
  void inorder() {
    inOrderHelper(this->root);
  }
  void postorder() {
    postOrderHelper(this->root);
  }
  NodePtr searchTree(int k) {
    return searchTreeHelper(this->root, k);
  }
  NodePtr minimum(NodePtr node) {
    while (node->left != TNULL) {
      node = node->left;
    }
    return node;
  }
  NodePtr maximum(NodePtr node) {
    while (node->right != TNULL) {
      node = node->right;
    }
    return node;
  }
  NodePtr successor(NodePtr x) {
    if (x->right != TNULL) {
      return minimum(x->right);
    }
    NodePtr y = x->parent;
    while (y != TNULL && x == y->right) {
      x = y;
      y = y->parent;
    }
    return y;
  }
  NodePtr predecessor(NodePtr x) {
    if (x->left != TNULL) {
      return maximum(x->left);
    }
    NodePtr y = x->parent;
    while (y != TNULL && x == y->left) {
      x = y;
      y = y->parent;
    }
    return y;
  }
  void leftRotate(NodePtr x) {
    NodePtr y = x->right;
    x->right = y->left;
    if (y->left != TNULL) {
      y->left->parent = x;
    }
    y->parent = x->parent;
    if (x->parent == nullptr) {
      this->root = y;
    } else if (x == x->parent->left) {
      x->parent->left = y;
    } else {
      x->parent->right = y;
    }
    y->left = x;
    x->parent = y;
  }
  void rightRotate(NodePtr x) {
    NodePtr y = x->left;
    x->left = y->right;
    if (y->right != TNULL) {
      y->right->parent = x;
    }
    y->parent = x->parent;
    if (x->parent == nullptr) {
      this->root = y;
    } else if (x == x->parent->right) {
      x->parent->right = y;
    } else {
      x->parent->left = y;
    }
    y->right = x;
    x->parent = y;
  }
  // Inserting a node
  void insert(int key) {
    NodePtr node = new Node;
    node->parent = nullptr;
    node->data = key;
    node->left = TNULL;
    node->right = TNULL;
    node->color = 1;
    NodePtr y = nullptr;
    NodePtr x = this->root;
    while (x != TNULL) {
      y = x;
      if (node->data < x->data) {
        x = x->left;
      } else {
        x = x->right;
      }
    }
    node->parent = y;
    if (y == nullptr) {
      root = node;
    } else if (node->data < y->data) {
      y->left = node;
    } else {
      y->right = node;
    }
    if (node->parent == nullptr) {
      node->color = 0;
      return;
    }
    if (node->parent->parent == nullptr) {
      return;
    }
    insertFix(node);
  }
  NodePtr getRoot() {
    return this->root;
  }
  void deleteNode(int data) {
    deleteNodeHelper(this->root, data);
  }
  void printTree() {
    if (root) {
      printHelper(this->root, "", true);
    }
  }
};
int main() {
  RedBlackTree V;
    V.insert(24);
    V.insert(33);
    V.insert(42);
    V.insert(51);
    V.insert(60);
    V.insert(40);
    V.insert(22);
  V.printTree();
  cout << endl
     << "After deleting an element" << endl;
  V.deleteNode(40);
  V.printTree();
}

輸出

R----33(BLACK)
   L----24(BLACK)
   |  L----22(RED)
   R----51(RED)
      L----42(BLACK)
      |  L----40(RED)
      R----60(BLACK)

After deleting an element
R----33(BLACK)
   L----24(BLACK)
   |  L----22(RED)
   R----51(RED)
      L----42(BLACK)
      R----60(BLACK)

// Implementing Red-Black Tree in Java
class Node {
    int data;
    Node parent;
    Node left;
    Node right;
    int color;
}
public class RedBlackTree {
    private Node root;
    private Node TNULL;

    // Preorder
    private void preOrderHelper(Node node) {
        if (node != TNULL) {
            System.out.print(node.data + " ");
            preOrderHelper(node.left);
            preOrderHelper(node.right);
        }
    }
    // Inorder
    private void inOrderHelper(Node node) {
        if (node != TNULL) {
            inOrderHelper(node.left);
            System.out.print(node.data + " ");
            inOrderHelper(node.right);
        }
    }

    // Post order
    private void postOrderHelper(Node node) {
        if (node != TNULL) {
            postOrderHelper(node.left);
            postOrderHelper(node.right);
            System.out.print(node.data + " ");
        }
    }

    // Search the tree
    private Node searchTreeHelper(Node node, int key) {
        if (node == TNULL || key == node.data) {
            return node;
        }

        if (key < node.data) {
            return searchTreeHelper(node.left, key);
        }
        return searchTreeHelper(node.right, key);
    }

    // Balance the tree after deletion of a node
    private void fixDelete(Node x) {
        Node s;
        while (x != root && x.color == 0) {
            if (x == x.parent.left) {
                s = x.parent.right;
                if (s.color == 1) {
                    s.color = 0;
                    x.parent.color = 1;
                    leftRotate(x.parent);
                    s = x.parent.right;
                }

                if (s.left.color == 0 && s.right.color == 0) {
                    s.color = 1;
                    x = x.parent;
                } else {
                    if (s.right.color == 0) {
                        s.left.color = 0;
                        s.color = 1;
                        rightRotate(s);
                        s = x.parent.right;
                    }

                    s.color = x.parent.color;
                    x.parent.color = 0;
                    s.right.color = 0;
                    leftRotate(x.parent);
                    x = root;
                }
            } else {
                s = x.parent.left;
                if (s.color == 1) {
                    s.color = 0;
                    x.parent.color = 1;
                    rightRotate(x.parent);
                    s = x.parent.left;
                }

                if (s.right.color == 0 && s.right.color == 0) {
                    s.color = 1;
                    x = x.parent;
                } else {
                    if (s.left.color == 0) {
                        s.right.color = 0;
                        s.color = 1;
                        leftRotate(s);
                        s = x.parent.left;
                    }

                    s.color = x.parent.color;
                    x.parent.color = 0;
                    s.left.color = 0;
                    rightRotate(x.parent);
                    x = root;
                }
            }
        }
        x.color = 0;
    }

    private void rbTransplant(Node u, Node v) {
        if (u.parent == null) {
            root = v;
        } else if (u == u.parent.left) {
            u.parent.left = v;
        } else {
            u.parent.right = v;
        }
        v.parent = u.parent;
    }

    private void deleteNodeHelper(Node node, int key) {
        Node z = TNULL;
        Node x, y;
        while (node != TNULL) {
            if (node.data == key) {
                z = node;
            }

            if (node.data <= key) {
                node = node.right;
            } else {
                node = node.left;
            }
        }

        if (z == TNULL) {
            System.out.println("Couldn't find key in the tree");
            return;
        }

        y = z;
        int yOriginalColor = y.color;
        if (z.left == TNULL) {
            x = z.right;
            rbTransplant(z, z.right);
        } else if (z.right == TNULL) {
            x = z.left;
            rbTransplant(z, z.left);
        } else {
            y = minimum(z.right);
            yOriginalColor = y.color;
            x = y.right;
            if (y.parent == z) {
                x.parent = y;
            } else {
                rbTransplant(y, y.right);
                y.right = z.right;
                y.right.parent = y;
            }

            rbTransplant(z, y);
            y.left = z.left;
            y.left.parent = y;
            y.color = z.color;
        }
        if (yOriginalColor == 0) {
            fixDelete(x);
        }
    }

    // Balance the node after insertion
    private void fixInsert(Node k) {
        Node u;
        while (k.parent.color == 1) {
            if (k.parent == k.parent.parent.right) {
                u = k.parent.parent.left;
                if (u.color == 1) {
                    u.color = 0;
                    k.parent.color = 0;
                    k.parent.parent.color = 1;
                    k = k.parent.parent;
                } else {
                    if (k == k.parent.left) {
                        k = k.parent;
                        rightRotate(k);
                    }
                    k.parent.color = 0;
                    k.parent.parent.color = 1;
                    leftRotate(k.parent.parent);
                }
            } else {
                u = k.parent.parent.right;

                if (u.color == 1) {
                    u.color = 0;
                    k.parent.color = 0;
                    k.parent.parent.color = 1;
                    k = k.parent.parent;
                } else {
                    if (k == k.parent.right) {
                        k = k.parent;
                        leftRotate(k);
                    }
                    k.parent.color = 0;
                    k.parent.parent.color = 1;
                    rightRotate(k.parent.parent);
                }
            }
            if (k == root) {
                break;
            }
        }
        root.color = 0;
    }

    private void printHelper(Node root, String indent, boolean last) {
        if (root != TNULL) {
            System.out.print(indent);
            if (last) {
                System.out.print("R----");
                indent += "   ";
            } else {
                System.out.print("L----");
                indent += "|  ";
            }

            String sColor = root.color == 1 ? "RED" : "BLACK";
            System.out.println(root.data + "(" + sColor + ")");
            printHelper(root.left, indent, false);
            printHelper(root.right, indent, true);
        }
    }

    public RedBlackTree() {
        TNULL = new Node();
        TNULL.color = 0;
        TNULL.left = null;
        TNULL.right = null;
        root = TNULL;
    }

    public void preorder() {
        preOrderHelper(this.root);
    }

    public void inorder() {
        inOrderHelper(this.root);
    }

    public void postorder() {
        postOrderHelper(this.root);
    }

    public Node searchTree(int k) {
        return searchTreeHelper(this.root, k);
    }

    public Node minimum(Node node) {
        while (node.left != TNULL) {
            node = node.left;
        }
        return node;
    }

    public Node maximum(Node node) {
        while (node.right != TNULL) {
            node = node.right;
        }
        return node;
    }

    public Node successor(Node x) {
        if (x.right != TNULL) {
            return minimum(x.right);
        }

        Node y = x.parent;
        while (y != TNULL && x == y.right) {
            x = y;
            y = y.parent;
        }
        return y;
    }

    public Node predecessor(Node x) {
        if (x.left != TNULL) {
            return maximum(x.left);
        }

        Node y = x.parent;
        while (y != TNULL && x == y.left) {
            x = y;
            y = y.parent;
        }

        return y;
    }

    public void leftRotate(Node x) {
        Node y = x.right;
        x.right = y.left;
        if (y.left != TNULL) {
            y.left.parent = x;
        }
        y.parent = x.parent;
        if (x.parent == null) {
            this.root = y;
        } else if (x == x.parent.left) {
            x.parent.left = y;
        } else {
            x.parent.right = y;
        }
        y.left = x;
        x.parent = y;
    }

    public void rightRotate(Node x) {
        Node y = x.left;
        x.left = y.right;
        if (y.right != TNULL) {
            y.right.parent = x;
        }
        y.parent = x.parent;
        if (x.parent == null) {
            this.root = y;
        } else if (x == x.parent.right) {
            x.parent.right = y;
        } else {
            x.parent.left = y;
        }
        y.right = x;
        x.parent = y;
    }

    public void insert(int key) {
        Node node = new Node();
        node.parent = null;
        node.data = key;
        node.left = TNULL;
        node.right = TNULL;
        node.color = 1;

        Node y = null;
        Node x = this.root;

        while (x != TNULL) {
            y = x;
            if (node.data < x.data) {
                x = x.left;
            } else {
                x = x.right;
            }
        }

        node.parent = y;
        if (y == null) {
            root = node;
        } else if (node.data < y.data) {
            y.left = node;
        } else {
            y.right = node;
        }

        if (node.parent == null) {
            node.color = 0;
            return;
        }

        if (node.parent.parent == null) {
            return;
        }

        fixInsert(node);
    }

    public Node getRoot() {
        return this.root;
    }

    public void deleteNode(int data) {
        deleteNodeHelper(this.root, data);
    }

    public void printTree() {
        printHelper(this.root, "", true);
    }

    public static void main(String[] args) {
        RedBlackTree V = new RedBlackTree();
        V.insert(24);
        V.insert(33);
        V.insert(42);
        V.insert(51);
        V.insert(60);
        V.insert(40);
        V.insert(22);
        V.printTree();

        System.out.println("\nAfter deleting an element:");
        V.deleteNode(40);
        V.printTree();
    }
}

輸出

R----33(BLACK)
   L----24(BLACK)
   |  L----22(RED)
R----51(RED)
L----42(BLACK)
|  L----40(RED)
      R----60(BLACK)
After deleting an element:
R----33(BLACK)
L----24(BLACK)
   |  L----22(RED)
R----51(RED)
L----42(BLACK)
R----60(BLACK)

#python program for Red black trees
import sys
# Node creation
class Node():
    def __init__(self, item):
        self.item = item
        self.parent = None
        self.left = None
        self.right = None
        self.color = 1
class RedBlackTree():
    def __init__(self):
        self.TNULL = Node(0)
        self.TNULL.color = 0
        self.TNULL.left = None
        self.TNULL.right = None
        self.root = self.TNULL
    # Preorder
    def pre_order_helper(self, node):
        if node != TNULL:
            sys.stdout.write(node.item + " ")
            self.pre_order_helper(node.left)
            self.pre_order_helper(node.right)
    # Inorder
    def in_order_helper(self, node):
        if node != TNULL:
            self.in_order_helper(node.left)
            sys.stdout.write(node.item + " ")
            self.in_order_helper(node.right)
    # Postorder
    def post_order_helper(self, node):
        if node != TNULL:
            self.post_order_helper(node.left)
            self.post_order_helper(node.right)
            sys.stdout.write(node.item + " ")
    # Search the tree
    def search_tree_helper(self, node, key):
        if node == TNULL or key == node.item:
            return node
        if key < node.item:
            return self.search_tree_helper(node.left, key)
        return self.search_tree_helper(node.right, key)
    # Balancing the tree after deletion
    def delete_fix(self, x):
        while x != self.root and x.color == 0:
            if x == x.parent.left:
                s = x.parent.right
                if s.color == 1:
                    s.color = 0
                    x.parent.color = 1
                    self.left_rotate(x.parent)
                    s = x.parent.right
                if s.left.color == 0 and s.right.color == 0:
                    s.color = 1
                    x = x.parent
                else:
                    if s.right.color == 0:
                        s.left.color = 0
                        s.color = 1
                        self.right_rotate(s)
                        s = x.parent.right
                    s.color = x.parent.color
                    x.parent.color = 0
                    s.right.color = 0
                    self.left_rotate(x.parent)
                    x = self.root
            else:
                s = x.parent.left
                if s.color == 1:
                    s.color = 0
                    x.parent.color = 1
                    self.right_rotate(x.parent)
                    s = x.parent.left

                if s.right.color == 0 and s.right.color == 0:
                    s.color = 1
                    x = x.parent
                else:
                    if s.left.color == 0:
                        s.right.color = 0
                        s.color = 1
                        self.left_rotate(s)
                        s = x.parent.left
                    s.color = x.parent.color
                    x.parent.color = 0
                    s.left.color = 0
                    self.right_rotate(x.parent)
                    x = self.root
        x.color = 0
    def __rb_transplant(self, u, v):
        if u.parent == None:
            self.root = v
        elif u == u.parent.left:
            u.parent.left = v
        else:
            u.parent.right = v
        v.parent = u.parent
    # Node deletion
    def delete_node_helper(self, node, key):
        z = self.TNULL
        while node != self.TNULL:
            if node.item == key:
                z = node
            if node.item <= key:
                node = node.right
            else:
                node = node.left
        if z == self.TNULL:
            print("Cannot find key in the tree")
            return
        y = z
        y_original_color = y.color
        if z.left == self.TNULL:
            x = z.right
            self.__rb_transplant(z, z.right)
        elif (z.right == self.TNULL):
            x = z.left
            self.__rb_transplant(z, z.left)
        else:
            y = self.minimum(z.right)
            y_original_color = y.color
            x = y.right
            if y.parent == z:
                x.parent = y
            else:
                self.__rb_transplant(y, y.right)
                y.right = z.right
                y.right.parent = y
            self.__rb_transplant(z, y)
            y.left = z.left
            y.left.parent = y
            y.color = z.color
        if y_original_color == 0:
            self.delete_fix(x)
    # Balance the tree after insertion
    def fix_insert(self, k):
        while k.parent.color == 1:
            if k.parent == k.parent.parent.right:
                u = k.parent.parent.left
                if u.color == 1:
                    u.color = 0
                    k.parent.color = 0
                    k.parent.parent.color = 1
                    k = k.parent.parent
                else:
                    if k == k.parent.left:
                        k = k.parent
                        self.right_rotate(k)
                    k.parent.color = 0
                    k.parent.parent.color = 1
                    self.left_rotate(k.parent.parent)
            else:
                u = k.parent.parent.right
                if u.color == 1:
                    u.color = 0
                    k.parent.color = 0
                    k.parent.parent.color = 1
                    k = k.parent.parent
                else:
                    if k == k.parent.right:
                        k = k.parent
                        self.left_rotate(k)
                    k.parent.color = 0
                    k.parent.parent.color = 1
                    self.right_rotate(k.parent.parent)
            if k == self.root:
                break
        self.root.color = 0
    # Printing the tree
    def __print_helper(self, node, indent, last):
        if node != self.TNULL:
            sys.stdout.write(indent)
            if last:
                sys.stdout.write("R----")
                indent += "     "
            else:
                sys.stdout.write("L----")
                indent += "|    "
            s_color = "RED" if node.color == 1 else "BLACK"
            print(str(node.item) + "(" + s_color + ")")
            self.__print_helper(node.left, indent, False)
            self.__print_helper(node.right, indent, True)
    def preorder(self):
        self.pre_order_helper(self.root)
    def inorder(self):
        self.in_order_helper(self.root)
    def postorder(self):
        self.post_order_helper(self.root)
    def searchTree(self, k):
        return self.search_tree_helper(self.root, k)
    def minimum(self, node):
        while node.left != self.TNULL:
            node = node.left
        return node
    def maximum(self, node):
        while node.right != self.TNULL:
            node = node.right
        return node
    def successor(self, x):
        if x.right != self.TNULL:
            return self.minimum(x.right)
        y = x.parent
        while y != self.TNULL and x == y.right:
            x = y
            y = y.parent
        return y
    def predecessor(self,  x):
        if (x.left != self.TNULL):
            return self.maximum(x.left)
        y = x.parent
        while y != self.TNULL and x == y.left:
            x = y
            y = y.parent
        return y
    def left_rotate(self, x):
        y = x.right
        x.right = y.left
        if y.left != self.TNULL:
            y.left.parent = x
        y.parent = x.parent
        if x.parent == None:
            self.root = y
        elif x == x.parent.left:
            x.parent.left = y
        else:
            x.parent.right = y
        y.left = x
        x.parent = y
    def right_rotate(self, x):
        y = x.left
        x.left = y.right
        if y.right != self.TNULL:
            y.right.parent = x
        y.parent = x.parent
        if x.parent == None:
            self.root = y
        elif x == x.parent.right:
            x.parent.right = y
        else:
            x.parent.left = y
        y.right = x
        x.parent = y
    def insert(self, key):
        node = Node(key)
        node.parent = None
        node.item = key
        node.left = self.TNULL
        node.right = self.TNULL
        node.color = 1
        y = None
        x = self.root
        while x != self.TNULL:
            y = x
            if node.item < x.item:
                x = x.left
            else:
                x = x.right
        node.parent = y
        if y == None:
            self.root = node
        elif node.item < y.item:
            y.left = node
        else:
            y.right = node
        if node.parent == None:
            node.color = 0
            return
        if node.parent.parent == None:
            return
        self.fix_insert(node)
    def get_root(self):
        return self.root
    def delete_node(self, item):
        self.delete_node_helper(self.root, item)
    def print_tree(self):
        self.__print_helper(self.root, "", True)
if __name__ == "__main__":
    V = RedBlackTree()
    V.insert(24)
    V.insert(33)
    V.insert(42)
    V.insert(51)
    V.insert(60)
    V.insert(40)
    V.insert(22)
    V.print_tree()
    print("\nAfter deleting an element")
    V.delete_node(40)
    V.print_tree()

輸出

R----33(BLACK)
     L----24(BLACK)
     |    L----22(RED)
R----51(RED)
          L----42(BLACK)
          |    L----40(RED)
          R----60(BLACK)

After deleting an element
R----33(BLACK)
     L----24(BLACK)
     |    L----22(RED)
     R----51(RED)
          L----42(BLACK)
          R----60(BLACK)
列印頁面
上一頁
下一頁
廣告
© . All rights reserved.