氣泡排序演算法

氣泡排序是一種簡單的排序演算法。這是一種基於比較的排序演算法，其中每對相鄰元素進行比較，如果它們沒有按順序排列，則交換元素。該演算法不適用於大型資料集，因為它的平均和最壞情況複雜度為 O(n²)，其中n是專案數。

氣泡排序演算法

氣泡排序是一種基本的排序演算法，它透過重複交換相鄰元素（如有必要）來工作。當不需要交換時，檔案就已排序。

我們假設list是一個包含n個元素的陣列。我們進一步假設swap函式交換給定陣列元素的值。

步驟 1 − 檢查輸入陣列中的第一個元素是否大於陣列中的下一個元素。

步驟 2 − 如果它更大，則交換這兩個元素；否則將指標向前移動到陣列中。

步驟 3 − 重複步驟 2，直到到達陣列的末尾。

步驟 4 − 檢查元素是否已排序；如果沒有，則從陣列的最後一個元素到第一個元素重複相同的過程（步驟 1 到步驟 3）。

步驟 5 − 達到的最終輸出是已排序的陣列。

Algorithm: Sequential-Bubble-Sort (A)
fori ← 1 to length [A] do
for j ← length [A] down-to i +1 do
   if A[A] < A[j-1] then
      Exchange A[j] ⟷ A[j-1]

虛擬碼

我們在演算法中觀察到，氣泡排序會比較每對陣列元素，除非整個陣列完全按升序排序。這可能會導致一些複雜性問題，例如，如果陣列不需要更多交換，因為所有元素都已經是升序的。

為了解決這個問題，我們使用一個標誌變數swapped，它將幫助我們檢視是否發生了任何交換。如果沒有發生交換，即陣列不需要更多處理即可排序，它將退出迴圈。

氣泡排序演算法的虛擬碼可以寫成如下：

voidbubbleSort(int numbers[], intarray_size){
   inti, j, temp;
   for (i = (array_size - 1); i>= 0; i--)
   for (j = 1; j <= i; j++)
   if (numbers[j-1] > numbers[j]){
      temp = numbers[j-1];
      numbers[j-1] = numbers[j];
      numbers[j] = temp;
   }
}

分析

這裡，比較次數為

       1 + 2 + 3 + ... + (n - 1) = n(n - 1)/2 = O(n2)

顯然，該圖顯示了氣泡排序的n²特性。

在此演算法中，比較次數與資料集無關，即提供的輸入元素是按排序順序、反向順序還是隨機順序。

記憶體需求

從上面描述的演算法可以看出，氣泡排序不需要額外的記憶體。

示例

我們以一個未排序的陣列為例。氣泡排序需要Ο(n2)時間，所以我們將其保持簡短和精確。

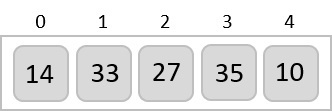
氣泡排序從最前面的兩個元素開始，比較它們以檢查哪個更大。

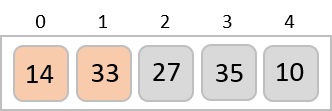
在這種情況下，值 33 大於 14，因此它已經位於排序位置。接下來，我們將 33 與 27 進行比較。

我們發現 27 小於 33，這兩個值必須交換。

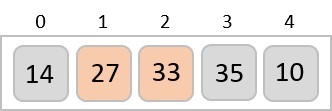
接下來我們比較 33 和 35。我們發現兩者都已位於排序位置。

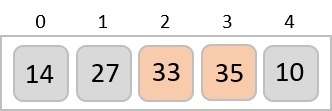
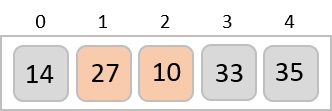
然後我們移動到接下來的兩個值，35 和 10。

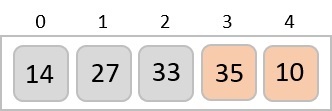
然後我們知道 10 小於 35。因此它們沒有排序。我們交換這些值。我們發現我們已經到達陣列的末尾。經過一次迭代後，陣列應該如下所示：

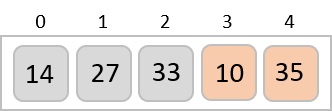
準確地說，我們現在展示了陣列在每次迭代後應該是什麼樣子。在第二次迭代之後，它應該如下所示：

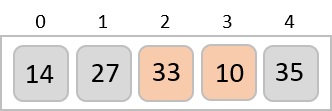
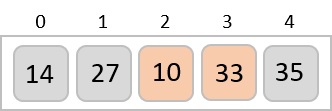
請注意，在每次迭代之後，至少有一個值移動到末尾。

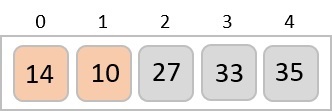
當不需要交換時，氣泡排序知道陣列已完全排序。

現在我們應該研究氣泡排序的一些實際方面。

實現

我們在原始演算法及其改進的虛擬碼中沒有解決的另一個問題是，在每次迭代之後，最高值都會沉澱在陣列的末尾。因此，下一次迭代不需要包含已排序的元素。為此，在我們的實現中，我們限制內迴圈以避免已排序的值。

#include <stdio.h>
void bubbleSort(int array[], int size){
   for(int i = 0; i<size; i++) {
      int swaps = 0; //flag to detect any swap is there or not
      for(int j = 0; j<size-i-1; j++) {
         if(array[j] > array[j+1]) { //when the current item is bigger than next
            int temp;
            temp = array[j];
            array[j] = array[j+1];
            array[j+1] = temp;
            swaps = 1; //set swap flag
         }
      }
      if(!swaps)
         break; // No swap in this pass, so array is sorted
   }
}
int main(){
   int n;
   n = 5;
   int arr[5] = {67, 44, 82, 17, 20}; //initialize an array 
   printf("Array before Sorting: ");
   for(int i = 0; i<n; i++)
      printf("%d ",arr[i]);
   printf("\n");
   bubbleSort(arr, n);
   printf("Array after Sorting: ");
   for(int i = 0; i<n; i++)
      printf("%d ", arr[i]);
   printf("\n");
}

Array before Sorting: 67 44 82 17 20 
Array after Sorting: 17 20 44 67 82 

#include<iostream>
using namespace std;
void bubbleSort(int *array, int size){
   for(int i = 0; i<size; i++) {
      int swaps = 0; //flag to detect any swap is there or not
      for(int j = 0; j<size-i-1; j++) {
         if(array[j] > array[j+1]) { //when the current item is bigger than next
            int temp;
            temp = array[j];
            array[j] = array[j+1];
            array[j+1] = temp;
            swaps = 1; //set swap flag
         }
      }
      if(!swaps)
         break; // No swap in this pass, so array is sorted
   }
}
int main(){
   int n;
   n = 5;
   int arr[5] = {67, 44, 82, 17, 20}; //initialize an array
   cout << "Array before Sorting: ";
   for(int i = 0; i<n; i++)
      cout << arr[i] << " ";
   cout << endl;
   bubbleSort(arr, n);
   cout << "Array after Sorting: ";
   for(int i = 0; i<n; i++)
      cout << arr[i] << " ";
   cout << endl;
}

Array before Sorting: 67 44 82 17 20 
Array after Sorting: 17 20 44 67 82

import java.io.*;
import java.util.*;
public class BubbleSort {
   public static void main(String args[]) {
      int n = 5;
      int[] arr = {67, 44, 82, 17, 20}; //initialize an array
      System.out.print("Array before Sorting: ");
      for(int i = 0; i<n; i++)
         System.out.print(arr[i] + " ");
      System.out.println();
      for(int i = 0; i<n; i++) {
         int swaps = 0; //flag to detect any swap is there or not
         for(int j = 0; j<n-i-1; j++) {
            if(arr[j] > arr[j+1]) { //when the current item is bigger than next
               int temp;
               temp = arr[j];
               arr[j] = arr[j+1];
               arr[j+1] = temp;
               swaps = 1; //set swap flag
            }
         }
         if(swaps == 0)
            break;
      }
      System.out.print("Array After Sorting: ");
      for(int i = 0; i<n; i++)
         System.out.print(arr[i] + " ");
      System.out.println();
   }
}

Array before Sorting: 67 44 82 17 20 
Array After Sorting: 17 20 44 67 82

def bubble_sort(array, size):
   for i in range(size):
      swaps = 0;
      for j in range(0, size-i-1):
         if(arr[j] > arr[j+1]):
            temp = arr[j];
            arr[j] = arr[j+1];
            arr[j+1] = temp;
            swaps = 1;
      if(swaps == 0):
         break;

arr = [67, 44, 82, 17, 20]
n = len(arr)
print("Array before Sorting: ")
print(arr)
bubble_sort(arr, n);
print("Array after Sorting: ")
print(arr)

Array before Sorting: 
[67, 44, 82, 17, 20]
Array after Sorting: 
[17, 20, 44, 67, 82]