Karger最小割演算法

Table of content
上一頁
下一頁

考慮現實世界的應用，例如影像分割，其中需要從影像中去除相機聚焦的物件。在這裡，每個畫素都被視為一個節點，並且這些畫素之間的容量被減少。遵循的演算法是最小割演算法。

最小割是指從圖（有向或無向）中移除最少數量的邊，使得圖被分割成多個單獨的圖或不相交的頂點集。

讓我們來看一個例子，以便更清楚地理解所獲得的不相交集

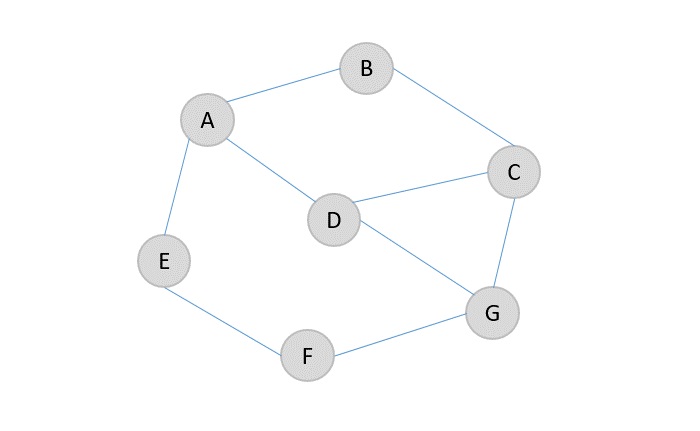
disjoint_sets

邊{A, E}和{F, G}是唯一容易從圖中移除的鬆散連線的邊。因此，該圖的最小割為2。

minimum_cut

移除邊A→E和F→G後，得到的圖是{A, B, C, D, G}和{E, F}。

removing_edges

Karger最小割演算法是一種用於查詢圖的最小割的隨機化演算法。它使用蒙特卡洛方法，因此預期在時間約束內執行，並且在達到輸出時誤差最小。但是，如果多次執行該演算法，則誤差機率會降低。Karger最小割演算法中使用的圖是無向無權圖。

Karger最小割演算法

Karger演算法將圖中的任意兩個節點合併成一個節點，稱為超節點。這兩個節點之間的邊被收縮，連線其他相鄰頂點的其他邊可以連線到超節點。

演算法

步驟1 - 從圖G中選擇任意一條隨機邊[u, v]進行收縮。

步驟2 - 合併頂點形成超節點，並將頂點的其他相鄰節點的邊連線到形成的超節點。刪除任何自環。

步驟3 - 重複此過程，直到收縮圖中只剩下兩個節點。

步驟4 - 連線這兩個節點的邊是最小割邊。

該演算法並不總是給出最佳輸出，因此需要多次重複該過程以降低錯誤機率。

虛擬碼

Kargers_MinCut(edge, V, E):
   v = V
   while(v > 2):
      i=Random integer in the range [0, E-1]
      s1=find(edge[i].u)
      s2=find(edge[i].v)
      if(s1 != s2):
         v = v-1
         union(u, v)
   mincut=0
   for(i in the range 0 to E-1):
      s1=find(edge[i].u)
      s2=find(edge[i].v)
      if(s1 != s2):
         mincut = mincut + 1
   return mincut

示例

將該演算法應用於無向無權圖G{V, E}，其中V和E分別是圖中存在的頂點和邊的集合，讓我們找到最小割：

undirected_unweighted

步驟1

選擇任意一條邊，例如A→B，並透過將兩個頂點合併成一個超節點來收縮該邊。將相鄰頂點的邊連線到超節點。刪除任何自環。

merging_two_vertices

步驟2

收縮另一條邊(A, B)→C，因此超節點將變成(A, B, C)，並且相鄰邊連線到新形成的更大的超節點。

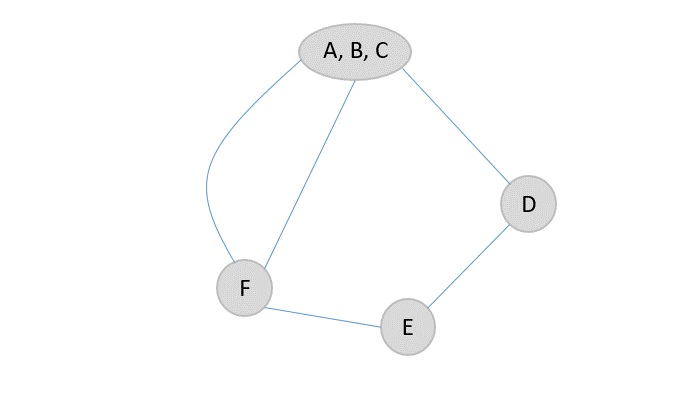
bigger_supernode

步驟3

節點D只有一條邊連線到超節點和一條相鄰邊，因此更容易收縮並將相鄰邊連線到新形成的超節點。

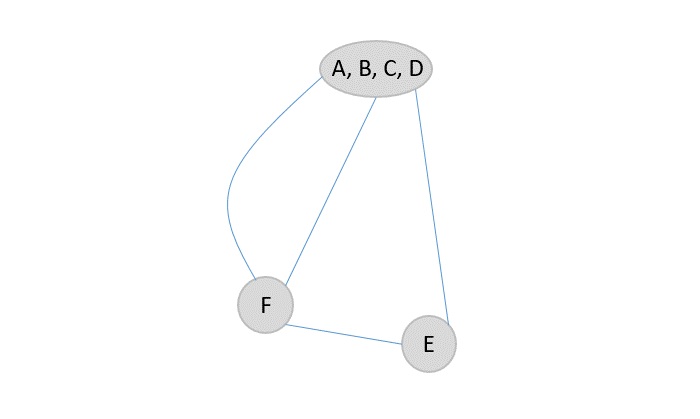
new_supernode_formed

步驟4

在F和E頂點中，F與超節點的連線更強，因此收縮連線F和(A, B, C, D)的邊。

F_strongly_bonded_supernode

步驟5

由於圖中只有兩個節點，邊的數量就是圖的最終最小割。在這種情況下，給定圖的最小割為2。

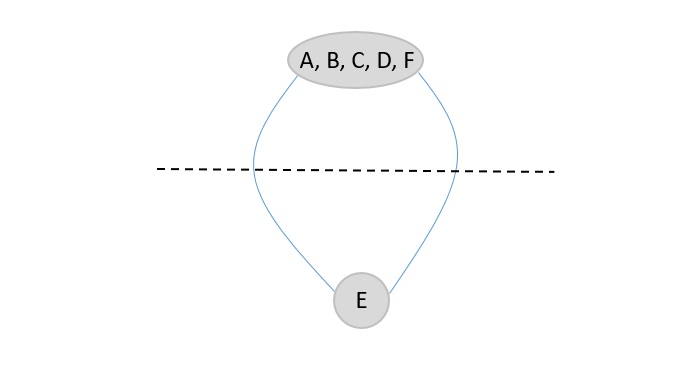
minimum_cut_graph

原始圖的最小割為2（E→D和E→F）。

實現

以下是上述方法在各種程式語言中的實現：

C C++ Java Python
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
struct Edge {
    int u, v;
};
struct Graph {
    int V;
    struct Edge* edges;
};
struct Graph* createGraph(int V, int E) {
    struct Graph* graph = (struct Graph*)malloc(sizeof(struct Graph));
    graph->V = V;
    graph->edges = (struct Edge*)malloc(E * sizeof(struct Edge));
    return graph;
}
int find(int parent[], int i) {
    if (parent[i] == i)
        return i;
    return find(parent, parent[i]);
}
void unionSets(int parent[], int rank[], int x, int y) {
    int xroot = find(parent, x);
    int yroot = find(parent, y);
    if (rank[xroot] < rank[yroot])
        parent[xroot] = yroot;
    else if (rank[xroot] > rank[yroot])
        parent[yroot] = xroot;
    else {
        parent[yroot] = xroot;
        rank[xroot]++;
    }
}
int kargerMinCut(struct Graph* graph) {
    int V = graph->V;
    int E = V * (V - 1) / 2;
    struct Edge* edges = graph->edges;

    int* parent = (int*)malloc(V * sizeof(int));
    int* rank = (int*)malloc(V * sizeof(int));
    for (int i = 0; i < V; i++) {
        parent[i] = i;
        rank[i] = 0;
    }
    int v = V;
    while (v > 2) {
        int randomIndex = rand() % E;
        int u = edges[randomIndex].u;
        int w = edges[randomIndex].v;
        int setU = find(parent, u);
        int setW = find(parent, w);
        if (setU != setW) {
            v--;
            unionSets(parent, rank, setU, setW);
        }
        edges[randomIndex] = edges[E - 1];
        E--;
    }
    int minCut = 0;
    for (int i = 0; i < E; i++) {
        int setU = find(parent, edges[i].u);
        int setW = find(parent, edges[i].v);
        if (setU != setW)
            minCut++;
    }
    free(parent);
    free(rank);
    return minCut;
}
int main() {
    int V = 4;
    int E = 5;
    struct Graph* graph = createGraph(V, E);
    graph->edges[0].u = 0;
    graph->edges[0].v = 1;
    graph->edges[1].u = 0;
    graph->edges[1].v = 2;
    graph->edges[2].u = 0;
    graph->edges[2].v = 3;
    graph->edges[3].u = 1;
    graph->edges[3].v = 3;
    graph->edges[4].u = 2;
    graph->edges[4].v = 3;
    srand(time(NULL));
    int minCut = kargerMinCut(graph);
    printf("Minimum Cut: %d\n", minCut);
    free(graph->edges);
    free(graph);
    return 0;
}

輸出

Minimum Cut: 2

#include <iostream>
#include <vector>
#include <cstdlib>
#include <ctime>
using namespace std;
struct Edge {
    int u, v;
};
class Graph
{
private:
    int V;
    vector<Edge> edges;
    int find(vector<int>& parent, int i)
    {
        if (parent[i] == i)
            return i;
        return find(parent, parent[i]);
    }
    void unionSets(vector<int>& parent, vector<int>& rank, int x, int y)
    {
        int xroot = find(parent, x);
        int yroot = find(parent, y);

        if (rank[xroot] < rank[yroot])
            parent[xroot] = yroot;
        else if (rank[xroot] > rank[yroot])
            parent[yroot] = xroot;
        else {
            parent[yroot] = xroot;
            rank[xroot]++;
        }
    }
public:
    Graph(int vertices) : V(vertices) {}
    void addEdge(int u, int v)
    {
        edges.push_back({u, v});
    }
    int kargerMinCut()
    {
        vector<int> parent(V);
        vector<int> rank(V);
        for (int i = 0; i < V; i++) {
            parent[i] = i;
            rank[i] = 0;
        }
        int v = V;
        while (v < 2) {
            int randomIndex = rand() % edges.size();
            int u = edges[randomIndex].u;
            int w = edges[randomIndex].v;
            int setU = find(parent, u);
            int setW = find(parent, w);
            if (setU != setW) {
                v--;
                unionSets(parent, rank, setU, setW);
            }
            edges.erase(edges.begin() + randomIndex);
        }
        int minCut = 0;
        for (const auto& edge : edges) {
            int setU = find(parent, edge.u);
            int setW = find(parent, edge.v);
            if (setU != setW)
                minCut++;
        }
        return minCut;
    }
};
int main()
{
    // Create a graph
    Graph g(4);
    g.addEdge(0, 1);
    g.addEdge(0, 2);
    g.addEdge(0, 3);
    g.addEdge(1, 3);
    g.addEdge(2, 3);
    // Set seed for random number generation
    srand(time(nullptr));
    // Find the minimum cut
    int minCut = g.kargerMinCut();
    cout << "Minimum Cut: " << minCut << endl;
    return 0;
}

輸出

Minimum Cut: 5

import java.util.ArrayList;
import java.util.List;
import java.util.Random;
class Edge {
    int u;
    int v;
    public Edge(int u, int v) {
        this.u = u;
        this.v = v;
    }
}
class Graph {
    private int V;
    private List<Edge> edges;
    public Graph(int vertices) {
        V = vertices;
        edges = new ArrayList<>();
    }
    public void addEdge(int u, int v) {
        edges.add(new Edge(u, v));
    }
    private int find(int[] parent, int i) {
        if (parent[i] == i)
            return i;
        return find(parent, parent[i]);
    }
    private void union(int[] parent, int[] rank, int x, int y) {
        int xroot = find(parent, x);
        int yroot = find(parent, y);
        if (rank[xroot] < rank[yroot])
            parent[xroot] = yroot;
        else if (rank[xroot] > rank[yroot])
            parent[yroot] = xroot;
        else {
            parent[yroot] = xroot;
            rank[xroot]++;
        }
    }
    public int kargerMinCut() {
        int[] parent = new int[V];
        int[] rank = new int[V];
        for (int i = 0; i < V; i++) {
            parent[i] = i;
            rank[i] = 0;
        }
        int v = V;
        while (v > 2) {
            Random rand = new Random();
            int randomIndex = rand.nextInt(edges.size());
            int u = edges.get(randomIndex).u;
            int w = edges.get(randomIndex).v;
            int setU = find(parent, u);
            int setW = find(parent, w);
            if (setU != setW) {
                v--;
                union(parent, rank, setU, setW);
            }
            edges.remove(randomIndex);
        }
        int minCut = 0;
        for (Edge edge : edges) {
            int setU = find(parent, edge.u);
            int setW = find(parent, edge.v);
            if (setU != setW)
                minCut++;
        }
        return minCut;
    }
}
public class Main {
    public static void main(String[] args) {
        // Create a graph
        Graph g = new Graph(4);
        g.addEdge(0, 1);
        g.addEdge(0, 2);
        g.addEdge(0, 3);
        g.addEdge(1, 3);
        g.addEdge(2, 3);
        // Set seed for random number generation
        Random rand = new Random();
        rand.setSeed(System.currentTimeMillis());
        // Find the minimum cut
        int minCut = g.kargerMinCut();
        System.out.println("Minimum Cut: " + minCut);
    }
}

輸出

Minimum Cut: 3

import random
class Graph:
    def __init__(self, vertices):
        self.V = vertices
        self.edges = []
    def addEdge(self, u, v):
        self.edges.append((u, v))
    def find(self, parent, i):
        if parent[i] == i:
            return i
        return self.find(parent, parent[i])
    def union(self, parent, rank, x, y):
        xroot = self.find(parent, x)
        yroot = self.find(parent, y)
        if rank[xroot] < rank[yroot]:
            parent[xroot] = yroot
        elif rank[xroot] > rank[yroot]:
            parent[yroot] = xroot
        else:
            parent[yroot] = xroot
            rank[xroot] += 1
    def kargerMinCut(self):
        parent = [i for i in range(self.V)]
        rank = [0] * self.V
        v = self.V
        while v > 2:
            i = random.randint(0, len(self.edges) - 1)
            u, w = self.edges[i]
            setU = self.find(parent, u)
            setW = self.find(parent, w)
            if setU != setW:
                v -= 1
                self.union(parent, rank, setU, setW)
            self.edges.pop(i)
        minCut = 0
        for u, w in self.edges:
            setU = self.find(parent, u)
            setW = self.find(parent, w)
            if setU != setW:
                minCut += 1
        return minCut
# Create a graph
g = Graph(4)
g.addEdge(0, 1)
g.addEdge(0, 2)
g.addEdge(0, 3)
g.addEdge(1, 3)
g.addEdge(2, 3)
# Set seed for random number generation
random.seed()
# Find the minimum cut
minCut = g.kargerMinCut()
print("Minimum Cut:", minCut)

輸出

Minimum Cut: 2
列印頁面
上一頁
下一頁
廣告