選擇排序演算法

選擇排序是一種簡單的排序演算法。這種排序演算法與插入排序一樣，是一種原地比較排序演算法，其中列表被分成兩個部分，排序部分在左側，未排序部分在右側。最初，排序部分為空，未排序部分是整個列表。

從未排序陣列中選擇最小元素，並將其與最左邊的元素交換，該元素成為排序陣列的一部分。此過程繼續將未排序陣列邊界向右移動一個元素。

此演算法不適用於大型資料集，因為其平均和最壞情況下的複雜度為O(n²)，其中n是專案的數量。

選擇排序演算法

這種型別的排序稱為選擇排序，因為它透過重複排序元素來工作。也就是說：我們首先找到陣列中最小的值並將其與第一個位置的元素交換，然後找到第二小的元素並將其與第二個位置的元素交換，我們繼續這個過程，直到整個陣列被排序。

1. Set MIN to location 0.
2. Search the minimum element in the list.
3. Swap with value at location MIN.
4. Increment MIN to point to next element.
5. Repeat until the list is sorted.

虛擬碼

Algorithm: Selection-Sort (A)
fori← 1 to n-1 do
   min j ←i;
   min x ← A[i]
   for j ←i + 1 to n do
      if A[j] < min x then
         min j ← j
         min x ← A[j]
   A[min j] ← A [i]
   A[i] ← min x

分析

選擇排序是最簡單的排序技術之一，它非常適合小型檔案。它有一個非常重要的應用，因為每個專案最多隻移動一次。

選擇排序是為排序具有非常大的物件（記錄）和小鍵的檔案而選擇的方法。如果陣列已經按降序排序，而我們想將其按升序排序，則會發生最壞的情況。

儘管如此，選擇排序演算法所需的時間對要排序的陣列的原始順序並不十分敏感：測試`A[j] < min` 在每種情況下執行的次數完全相同。

選擇排序花費大部分時間試圖在陣列的未排序部分中找到最小元素。它清楚地顯示了選擇排序和氣泡排序之間的相似性。

• 氣泡排序在每個階段選擇剩餘的最大元素，但浪費了一些努力來對陣列的未排序部分進行排序。

• 選擇排序在最壞情況和平均情況下都是二次的，並且不需要額外的記憶體。

對於從1到n - 1的每個i，有一個交換和n - i次比較，所以總共有n - 1次交換和

(n − 1) + (n − 2) + ... + 2 + 1 = n(n − 1)/2 次比較。

無論輸入資料是什麼，這些觀察結果都成立。

在最壞的情況下，這可能是二次的，但在平均情況下，這個數量是O(n log n)。這意味著選擇排序的執行時間對輸入並不十分敏感。

示例

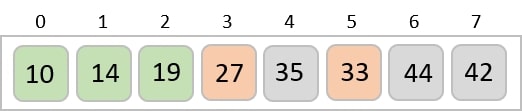
考慮以下所示陣列為例。

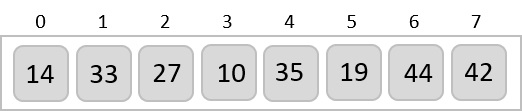
對於排序列表中的第一個位置，整個列表都會順序掃描。當前儲存 14 的第一個位置，我們搜尋整個列表並發現 10 是最小值。

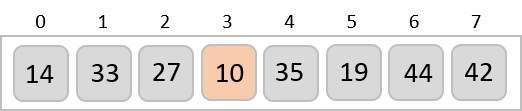
因此，我們將 14 替換為 10。經過一次迭代後，恰好是列表中最小值的 10 出現在排序列表的第一個位置。

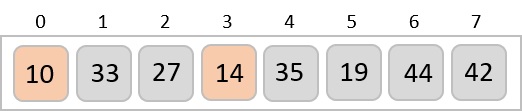
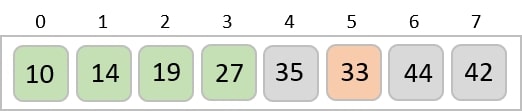
對於第二個位置（其中駐留 33），我們以線性方式開始掃描列表的其餘部分。

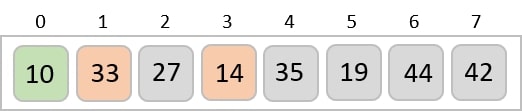
我們發現 14 是列表中第二小的值，它應該出現在第二個位置。我們交換這些值。

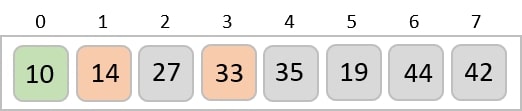
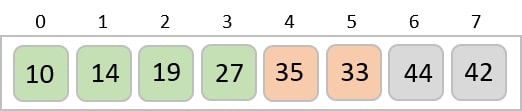
經過兩次迭代後，兩個最小值以排序的方式位於開頭。

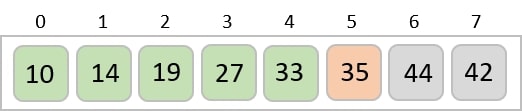
相同的過程應用於陣列中的其餘專案 -

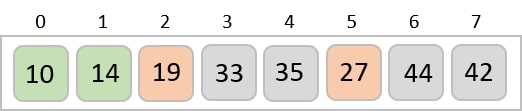
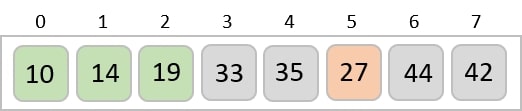
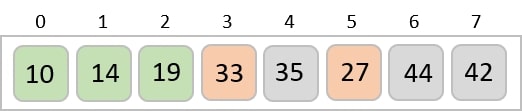
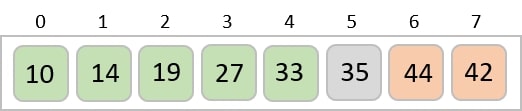
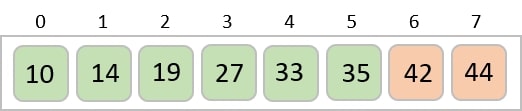
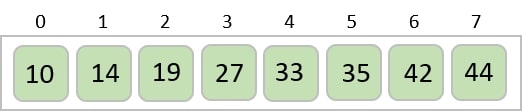
實現

選擇排序演算法在下面用四種不同的程式語言實現。給定的程式選擇陣列的最小數字並將其與第一個索引中的元素交換。第二個最小數字與第二個索引中存在的元素交換。這個過程持續到陣列結束。

#include <stdio.h>
void selectionSort(int array[], int size){
   int i, j, imin;
   for(i = 0; i<size-1; i++) {
      imin = i; //get index of minimum data
      for(j = i+1; j<size; j++)
         if(array[j] < array[imin])
            imin = j;
      
      //placing in correct position
      int temp;
      temp = array[i];
      array[i] = array[imin];
      array[imin] = temp;
   }
}
int main(){
   int n;
   n = 5;
   int arr[5] = {12, 19, 55, 2, 16}; // initialize the array
   printf("Array before Sorting: ");
   for(int i = 0; i<n; i++)
      printf("%d ",arr[i]);
   printf("\n");
   selectionSort(arr, n);
   printf("Array after Sorting: ");
   for(int i = 0; i<n; i++)
      printf("%d ", arr[i]);
   printf("\n");
}

Array before Sorting: 12 19 55 2 16
Array after Sorting: 2 12 16 19 55

#include<iostream>
using namespace std;
void swapping(int &a, int &b) {  //swap the content of a and b
   int temp;
   temp = a;
   a = b;
   b = temp;
}
void selectionSort(int *array, int size){
   int i, j, imin;
   for(i = 0; i<size-1; i++) {
      imin = i; //get index of minimum data
      for(j = i+1; j<size; j++)
         if(array[j] < array[imin])
            imin = j;

      //placing in correct position
      swap(array[i], array[imin]);
   }
}
int main(){
   int n;
   n = 5;
   int arr[5] = {12, 19, 55, 2, 16}; // initialize the array
   cout << "Array before Sorting: ";
   for(int i = 0; i<n; i++)
      cout << arr[i] << " ";
   cout << endl;
   selectionSort(arr, n);
   cout << "Array after Sorting: ";
   for(int i = 0; i<n; i++)
      cout << arr[i] << " ";
   cout << endl;
}

Array before Sorting: 12 19 55 2 16
Array after Sorting: 2 12 16 19 55

import java.io.*;
public class SelectionSort {
   public static void main(String args[]) {
      int n = 5;
      int[] arr = {12, 19, 55, 2, 16}; //initialize an array
      System.out.print("Array before Sorting: ");
      for(int i = 0; i<n; i++)
         System.out.print(arr[i] + " ");
      System.out.println();
      int imin;
      for(int i = 0; i<n-1; i++) {
         imin = i; //get index of minimum data
         for(int j = i+1; j<n; j++)
            if(arr[j] < arr[imin])
               imin = j;
         
         //placing in correct position
         int temp;
         temp = arr[i];
         arr[i] = arr[imin];
         arr[imin] = temp;
      }
      System.out.print("Array After Sorting: ");
      for(int i = 0; i<n; i++)
         System.out.print(arr[i] + " ");
      System.out.println();
   }
}

Array before Sorting: 12 19 55 2 16 

Array After Sorting: 2 12 16 19 55

def insertion_sort(array, size):
   for i in range(size):
      imin = i
      for j in range(i+1, size):
         if arr[j] < arr[imin]:
            imin = j
      temp = array[i];
      array[i] = array[imin];
      array[imin] = temp;

arr = [12, 19, 55, 2, 16]
n = len(arr)
print("Array before Sorting: ")
print(arr)
insertion_sort(arr, n);
print("Array after Sorting: ")
print(arr)

Array before Sorting: 
[12, 19, 55, 2, 16]
Array after Sorting: 
[2, 12, 16, 19, 55]