集合覆蓋問題

Table of content
上一頁
下一頁

集合覆蓋演算法為許多現實世界中的資源分配問題提供瞭解決方案。例如，考慮一家航空公司為每架飛機分配機組人員，以確保他們有足夠的人員來滿足旅程的要求。他們會考慮航班時間、持續時間、中途停留以及機組人員的可用性，以便將他們分配到航班。這就是集合覆蓋演算法發揮作用的地方。

給定一個包含一些元素的全集 U，所有這些元素都被分成子集。將這些子集的集合視為 S = {S1, S2, S3, S4... Sn}，集合覆蓋演算法找到最少的子集數量，使得它們覆蓋全集中的所有元素。

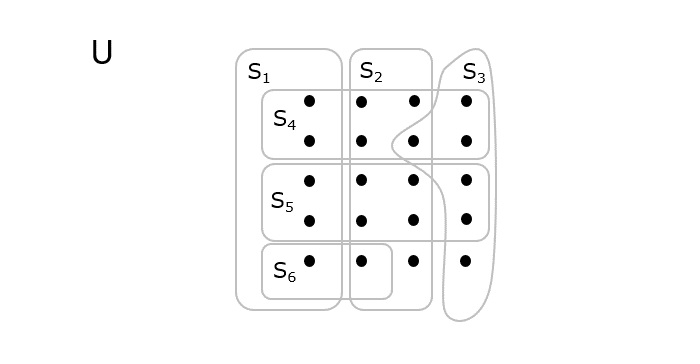
universal_set

如上圖所示，點表示存在於全集 U 中的元素，這些元素被分成不同的集合 S = {S1, S2, S3, S4, S5, S6}。為了覆蓋所有元素，需要選擇的最小集合數將是最優輸出 = {S1, S2, S3}。

集合覆蓋演算法

集合覆蓋演算法將集合的集合作為輸入，並返回包含所有全集元素所需的最小集合數。

集合覆蓋問題是一個 NP-Hard 問題，並且是一個 2-逼近貪心演算法。

演算法

步驟 1 - 初始化 Output = {}，其中 Output 表示輸出元素集。

步驟 2 - 當 Output 集不包含全集中的所有元素時，執行以下操作：

  • 使用公式 $\frac{Cost\left ( S_{i} \right )}{S_{i}-Output}$ 查詢全集中的每個子集的成本效益。

  • 找到每次迭代中成本效益最低的子集。將子集新增到 Output 集。

步驟 3 - 重複步驟 2，直到宇宙中沒有剩餘元素。達到的輸出是最終的 Output 集。

虛擬碼

APPROX-GREEDY-SET_COVER(X, S)
   U = X
   OUTPUT = ф
   while U ≠ ф
      select Si Є S which has maximum |Si∩U|
   U = U – S
   OUTPUT = OUTPUT∪ {Si}
return OUTPUT

分析

假設元素總數等於集合總數（|X| = |S|），則程式碼執行時間為 O(|X|3)

示例

Set_Cover_Algorithm

讓我們來看一個更詳細地描述集合覆蓋問題近似演算法的例子

S1 = {1, 2, 3, 4}                cost(S1) = 5
S2 = {2, 4, 5, 8, 10}            cost(S2) = 10
S3 = {1, 3, 5, 7, 9, 11, 13}     cost(S3) = 20
S4 = {4, 8, 12, 16, 20}          cost(S4) = 12
S5 = {5, 6, 7, 8, 9}             cost(S5) = 15

步驟 1

輸出集 Output = ф

找到輸出集中沒有元素時每個集合的成本效益，

S1 = cost(S1) / (S1 – Output) = 5 / (4 – 0)
S2 = cost(S2) / (S2 – Output) = 10 / (5 – 0)
S3 = cost(S3) / (S3 – Output) = 20 / (7 – 0)
S4 = cost(S4) / (S4 – Output) = 12 / (5 – 0)
S5 = cost(S5) / (S5 – Output) = 15 / (5 – 0)

本次迭代中，S1 的成本效益最低，因此，新增到輸出集的子集 Output = {S1}，其元素為 {1, 2, 3, 4}。

步驟 2

找到輸出集中新元素的每個集合的成本效益，

S2 = cost(S2) / (S2 – Output) = 10 / (5 – 4)
S3 = cost(S3) / (S3 – Output) = 20 / (7 – 4)
S4 = cost(S4) / (S4 – Output) = 12 / (5 – 4)
S5 = cost(S5) / (S5 – Output) = 15 / (5 – 4)

本次迭代中，S3 的成本效益最低，因此，新增到輸出集的子集 Output = {S1, S3}，其元素為 {1, 2, 3, 4, 5, 7, 9, 11, 13}。

步驟 3

找到輸出集中新元素的每個集合的成本效益，

S2 = cost(S2) / (S2 – Output) = 10 / |(5 – 9)|
S4 = cost(S4) / (S4 – Output) = 12 / |(5 – 9)|
S5 = cost(S5) / (S5 – Output) = 15 / |(5 – 9)|

本次迭代中，S2 的成本效益最低，因此，新增到輸出集的子集 Output = {S1, S3, S2}，其元素為 {1, 2, 3, 4, 5, 7, 8, 9, 10, 11, 13}。

步驟 4

找到輸出集中新元素的每個集合的成本效益，

S4 = cost(S4) / (S4 – Output) = 12 / |(5 – 11)|
S5 = cost(S5) / (S5 – Output) = 15 / |(5 – 11)|

本次迭代中，S4 的成本效益最低，因此，新增到輸出集的子集 Output = {S1, S3, S2, S4}，其元素為 {1, 2, 3, 4, 5, 7, 8, 9, 10, 11, 12, 13, 16, 20}。

步驟 5

找到輸出集中新元素的每個集合的成本效益，

S5 = cost(S5) / (S5 – Output) = 15 / |(5 – 14)|

本次迭代中，S5 的成本效益最低，因此，新增到輸出集的子集 Output = {S1, S3, S2, S4, S5}，其元素為 {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 16, 20}。

最終覆蓋有限全集中的所有元素的輸出為 Output = {S1, S3, S2, S4, S5}。

實現

以下是上述方法在各種程式語言中的實現：

C C++ Java Python
#include <stdio.h>
#define MAX_SETS 100
#define MAX_ELEMENTS 1000
int setCover(int X[], int S[][MAX_ELEMENTS], int numSets, int numElements, int output[]) {
   int U[MAX_ELEMENTS];
   for (int i = 0; i < numElements; i++) {
      U[i] = X[i];
   }
   int selectedSets[MAX_SETS];
   for (int i = 0; i < MAX_SETS; i++) {
      selectedSets[i] = 0; // Initialize all to 0 (not selected)
   }
   int outputIdx = 0;
   while (outputIdx < numSets) {  // Ensure we don't exceed the maximum number of sets
      int maxIntersectionSize = 0;
      int selectedSetIdx = -1;
      // Find the set Si with the maximum intersection with U
      for (int i = 0; i < numSets; i++) {
         if (selectedSets[i] == 0) { // Check if the set is not already selected
            int intersectionSize = 0;
            for (int j = 0; j < numElements; j++) {
               if (U[j] && S[i][j]) {
                  intersectionSize++;
               }
            }
            if (intersectionSize > maxIntersectionSize) {
               maxIntersectionSize = intersectionSize;
               selectedSetIdx = i;
            }
         }
      }
      // If no set found, break from the loop
      if (selectedSetIdx == -1) {
          break;
      }
      // Mark the selected set as "selected" in the array
      selectedSets[selectedSetIdx] = 1;
      // Remove the elements covered by the selected set from U
      for (int j = 0; j < numElements; j++) {
          U[j] = U[j] - S[selectedSetIdx][j];
      }
      // Add the selected set to the output
      output[outputIdx++] = selectedSetIdx;
   }
   return outputIdx;
}
int main() {
   int X[MAX_ELEMENTS] = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
   int S[MAX_SETS][MAX_ELEMENTS] = {
      {1, 1, 0, 0, 0, 0, 0, 0, 0, 0},
      {0, 1, 1, 1, 0, 0, 0, 0, 0, 0},
      {0, 0, 0, 1, 1, 1, 0, 0, 0, 0},
      {0, 0, 0, 0, 0, 1, 1, 1, 0, 0},
      {0, 0, 0, 0, 0, 0, 0, 1, 1, 1}
   };
   int numSets = 5;
   int numElements = 10;
   int output[MAX_SETS];
   int numSelectedSets = setCover(X, S, numSets, numElements, output);
   printf("Selected Sets: ");
   for (int i = 0; i < numSelectedSets; i++) {
      printf("%d ", output[i]);
   }
   printf("\n");
   return 0;
}

輸出

Selected Sets: 1 2 3 4 0

#include <iostream>
#include <vector>
using namespace std;
#define MAX_SETS 100
#define MAX_ELEMENTS 1000
// Function to find the set cover using the Approximate Greedy Set Cover algorithm
int setCover(int X[], int S[][MAX_ELEMENTS], int numSets, int numElements, int output[])
{
   int U[MAX_ELEMENTS];
   for (int i = 0; i < numElements; i++) {
      U[i] = X[i];
   }
   int selectedSets[MAX_SETS];
   for (int i = 0; i < MAX_SETS; i++) {
      selectedSets[i] = 0; // Initialize all to 0 (not selected)
   }
   int outputIdx = 0;
   while (outputIdx < numSets) {  // Ensure we don't exceed the maximum number of sets
      int maxIntersectionSize = 0;
      int selectedSetIdx = -1;
      // Find the set Si with maximum intersection with U
      for (int i = 0; i < numSets; i++) {
         if (selectedSets[i] == 0) { // Check if the set is not already selected
            int intersectionSize = 0;
            for (int j = 0; j < numElements; j++) {
               if (U[j] && S[i][j]) {
                  intersectionSize++;
               }
            }
            if (intersectionSize > maxIntersectionSize) {
               maxIntersectionSize = intersectionSize;
               selectedSetIdx = i;
            }
         }
      }
      // If no set found, break from the loop
      if (selectedSetIdx == -1) {
         break;
      }
      // Mark the selected set as "selected" in the array
      selectedSets[selectedSetIdx] = 1;
      // Remove the elements covered by the selected set from U
      for (int j = 0; j < numElements; j++) {
         U[j] = U[j] - S[selectedSetIdx][j];
      }
      // Add the selected set to the output
      output[outputIdx++] = selectedSetIdx;
   }
   return outputIdx;
}
int main()
{
   int X[MAX_ELEMENTS] = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
   int S[MAX_SETS][MAX_ELEMENTS] = {
      {1, 1, 0, 0, 0, 0, 0, 0, 0, 0},
      {0, 1, 1, 1, 0, 0, 0, 0, 0, 0},
      {0, 0, 0, 1, 1, 1, 0, 0, 0, 0},
      {0, 0, 0, 0, 0, 1, 1, 1, 0, 0},
      {0, 0, 0, 0, 0, 0, 0, 1, 1, 1}
   };
   int numSets = 5;
   int numElements = 10;
   int output[MAX_SETS];
   int numSelectedSets = setCover(X, S, numSets, numElements, output);
   cout << "Selected Sets: ";
   for (int i = 0; i < numSelectedSets; i++) {
       cout << output[i] << " ";
   }
   cout << endl;
   return 0;
}

輸出

Selected Sets: 1 2 3 4 0 

import java.util.*;
public class SetCover {
   public static List<Integer> setCover(int[] X, int[][] S) {
      Set<Integer> U = new HashSet<>();
      for (int x : X) {
         U.add(x);
      }
      List<Integer> output = new ArrayList<>();
      while (!U.isEmpty()) {
         int maxIntersectionSize = 0;
         int selectedSetIdx = -1;
         for (int i = 0; i < S.length; i++) {
            int intersectionSize = 0;
            for (int j = 0; j < S[i].length; j++) {
               if (U.contains(S[i][j])) {
                  intersectionSize++;
               }
            }
            if (intersectionSize > maxIntersectionSize) {
               maxIntersectionSize = intersectionSize;
               selectedSetIdx = i;
            }
         }
         if (selectedSetIdx == -1) {
            break;
         }
         for (int j = 0; j < S[selectedSetIdx].length; j++) {
            U.remove(S[selectedSetIdx][j]);
         }
         output.add(selectedSetIdx);
      }
      return output;
   }
public static void main(String[] args) {
   int[] X = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
   int[][] S = {
      {1, 2},
      {2, 3, 4},
      {4, 5, 6},
      {6, 7, 8},
      {8, 9, 10}
   };
   List<Integer> selectedSets = setCover(X, S);
   System.out.print("Selected Sets: ");
   for (int idx : selectedSets) {
      System.out.print(idx + " ");
   }
   System.out.println();
   }
}

輸出

Selected Sets: 1 3 4 0 2 

def set_cover(X, S):
    U = set(X)
    output = []
    while U:
        max_intersection_size = 0
        selected_set_idx = -1
        for i, s in enumerate(S):
            intersection_size = len(U.intersection(s))
            if intersection_size > max_intersection_size:
                max_intersection_size = intersection_size
                selected_set_idx = i
        if selected_set_idx == -1:
            break
        U = U - set(S[selected_set_idx])
        output.append(selected_set_idx)
    return output
if __name__ == "__main__":
    X = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
    S = [
        {1, 2},
        {2, 3, 4},
        {4, 5, 6},
        {6, 7, 8},
        {8, 9, 10}
    ]
    selected_sets = set_cover(X, S)
    print("Selected Sets:", selected_sets)

輸出

Selected Sets: 1 3 4 0 2
列印頁面
上一頁
下一頁
廣告