Boyer-Moore 演算法

上一頁
下一頁

用於模式匹配的Boyer-Moore演算法

Boyer-Moore演算法用於確定給定模式是否存在於指定文字中。它採用了一種反向的模式搜尋/匹配方法。在一個給定字串中搜索特定模式的任務被稱為模式搜尋問題。例如，如果文字是“THIS IS A SAMPLE TEXT”，模式是“TEXT”，則輸出應為10，這是模式在給定文字中第一次出現的索引。

該演算法由Robert Boyer和J Strother Moore於1977年開發。它被認為是最有效和最廣泛使用的模式匹配演算法。

Boyer-Moore演算法是如何工作的？

在前面的章節中，我們已經看到了解決這個問題的簡單方法，它涉及到逐個滑動模式覆蓋文字，並比較每個字元。然而，這種方法非常慢，因為它需要O(n*m)時間，其中'n'是文字的長度，'m'是模式的長度。Boyer-Moore演算法透過預處理模式並使用兩種啟發式方法來跳過一些不可能匹配的比較來改進這一點。

這兩種啟發式方法如下：

  • 壞字元啟發式 - 此啟發式方法使用一個表來儲存模式中每個字元的最後出現位置。當文字中某個字元（壞字元）發生不匹配時，演算法會檢查此字元是否出現在模式中。如果出現，則它會移動模式，使模式中該字元的最後出現位置與文字中的壞字元對齊。如果沒有，則它會將模式移過壞字元。

  • 好字尾啟發式 - 此啟發式方法使用另一個表來儲存當壞字元啟發式方法失敗時的移位資訊。在這種情況下，我們會在模式內查詢，直到壞字元變成文字的好字尾。然後我們繼續移動以查詢給定的模式。

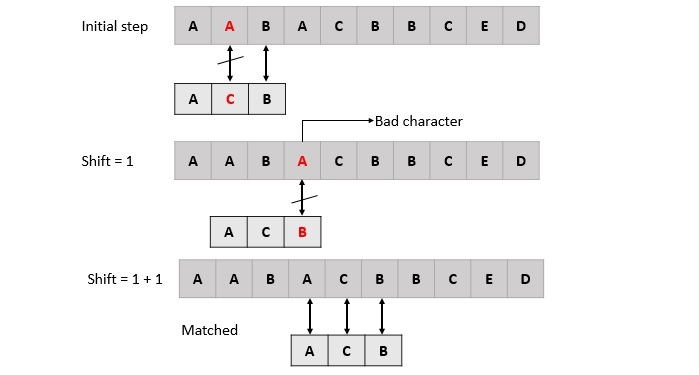
Boyer Solution

Boyer-Moore演算法透過在每一步選擇它們建議的最大位移來組合這兩種啟發式方法。在這個過程中，子串或模式是從模式的最後一個字元開始搜尋的。當主字串的子串與模式的子串匹配時，它會移動以查詢匹配子串的其他出現位置。如果發生不匹配，它會應用啟發式方法並相應地移動模式。當找到完全匹配或到達文字末尾時，演算法停止。

Boyer-Moore演算法的最壞情況時間複雜度為O(nm)，但是，它的效能可能遠高於此。事實上，在某些情況下，它可以達到O(n/m)的亞線性時間複雜度，這意味著它可以在不比較文字中某些字元的情況下跳過這些字元。當模式沒有重複字元或具有較大的字母表大小時，就會發生這種情況。

為了說明Boyer-Moore演算法是如何工作的，讓我們考慮一個例子：

Input:
main String: "AABAAABCEDBABCDDEBC" 
pattern: "ABC"
Output:
Pattern found at position: 5
Pattern found at position: 11

示例

在下面的示例中，我們將演示Boyer-Moore演算法在各種程式語言中的工作方式。

C語言 C++ Java Python
#include<stdio.h> 
#include<string.h> 
// Function for full suffix match
void computeFullShift(int shiftArr[], int longSuffArr[], char patrn[], int n) {
   int i = n;
   int j = n+1;
   longSuffArr[i] = j;
   while(i > 0) {
      // Searching right if (i-1)th and (j-1)th item are not the same
      while(j <= n && patrn[i-1] != patrn[j-1] ) {
          // to shift pattern from i to j
         if(shiftArr[j] == 0) {
            shiftArr[j] = j-i; 
         }
         // Updating long suffix value
         j = longSuffArr[j]; 
      }
      i--;
      j--;
      longSuffArr[i] = j;
   }  
}
// Function for good suffix match
void computeGoodSuffix(int shiftArr[], int longSuffArr[], char patrn[], int n) {
   int j;
   j = longSuffArr[0];
   // Looping through the pattern
   for(int i = 0; i<n; i++) {
      // setting shift to long suffix value
      if(shiftArr[i] == 0) {
         shiftArr[i] = j; 
         if(i == j) {
            // Updating long suffix value
            j = longSuffArr[j]; 
         }
      }
   }
}
// Function for searching the pattern
void searchPattern(char orgnStr[], char patrn[], int array[], int *index) {
   // length of the pattern
   int patLen = strlen(patrn); 
   // length of main string
   int strLen = strlen(orgnStr);
   int longerSuffArray[patLen+1];
   int shiftArr[patLen + 1];
   // Initializing shift array elements to 0
   for(int i = 0; i<=patLen; i++) {
      shiftArr[i] = 0;
   }
   // Calling computeFullShift function
   computeFullShift(shiftArr, longerSuffArray, patrn, patLen); 
   // Calling computeGoodSuffix function
   computeGoodSuffix(shiftArr, longerSuffArray, patrn, patLen); 
   int shift = 0;
   while(shift <= (strLen - patLen)) {
      int j = patLen - 1;
      // decrement j when pattern and main string character is matching
      while(j >= 0 && patrn[j] == orgnStr[shift+j]) {
         j--; 
      }
      if(j < 0) {
         (*index)++;
         // to store the position where pattern is found
         array[(*index)] = shift; 
         shift += shiftArr[0];
      }else {
          shift += shiftArr[j+1];
      }
   }
}
int main() {
   // original string    
   char orgnStr[] = "AABAAABCEDBABCDDEBC"; 
   // Pattern to be searched
   char patrn[] = "ABC"; 
   // Array to store the positions where pattern is found
   int locArray[strlen(orgnStr)]; 
   int index = -1;
   // Calling the searchPattern function
   searchPattern(orgnStr, patrn, locArray, &index); 
   // Printing the positions where pattern is found
   for(int i = 0; i <= index; i++) {
      printf("Pattern found at position: %d\n", locArray[i]);
   }
   return 0;
}

#include<iostream> 
using namespace std; 
// Function for full suffix match
void computeFullShift(int shiftArr[], int longSuffArr[], string patrn) {
   // length of pattern
   int n = patrn.size(); 
   int i = n;
   int j = n+1;
   longSuffArr[i] = j;
   while(i > 0) {
      // Searching right if (i-1)th and (j-1)th item are not the same
      while(j <= n && patrn[i-1] != patrn[j-1] ) {
          // to shift pattern from i to j
         if(shiftArr[j] == 0) {
            shiftArr[j] = j-i; 
         }
         // Updating long suffix value
         j = longSuffArr[j]; 
      }
      i--;
      j--;
      longSuffArr[i] = j;
   }  
}
// Function for good suffix match
void computeGoodSuffix(int shiftArr[], int longSuffArr[], string patrn) {
   // length of the pattern
   int n = patrn.size(); 
   int j;
   j = longSuffArr[0];
   // Looping through the pattern
   for(int i = 0; i<n; i++) {
      // setting shift to long suffix value
      if(shiftArr[i] == 0) {
         shiftArr[i] = j; 
         if(i == j) {
            // Updating long suffix value
            j = longSuffArr[j]; 
         }
      }
   }
}
// Function for searching the pattern
void searchPattern(string orgnStr, string patrn, int array[], int *index) {
   // length of the pattern
   int patLen = patrn.size(); 
   // length of main string
   int strLen = orgnStr.size();
   int longerSuffArray[patLen+1];
   int shiftArr[patLen + 1];
   // Initializing shift array elements to 0
   for(int i = 0; i<=patLen; i++) {
      shiftArr[i] = 0;
   }
   // Calling computeFullShift function
   computeFullShift(shiftArr, longerSuffArray, patrn); 
   // Calling computeGoodSuffix function
   computeGoodSuffix(shiftArr, longerSuffArray, patrn); 
   int shift = 0;
   while(shift <= (strLen - patLen)) {
      int j = patLen - 1;
      // decrement j when pattern and main string character is matching
      while(j >= 0 && patrn[j] == orgnStr[shift+j]) {
         j--; 
      }
      if(j < 0) {
         (*index)++;
         // to store the position where pattern is found
         array[(*index)] = shift; 
         shift += shiftArr[0];
      }else {
          shift += shiftArr[j+1];
      }
   }
}
int main() {
   // original string    
   string orgnStr = "AABAAABCEDBABCDDEBC"; 
   // Pattern to be searched
   string patrn = "ABC"; 
   // Array to store the positions where pattern is found
   int locArray[orgnStr.size()]; 
   int index = -1;
   // Calling the searchPattern function
   searchPattern(orgnStr, patrn, locArray, &index); 
   // Printing the positions where pattern is found
   for(int i = 0; i <= index; i++) {
      cout << "Pattern found at position: " << locArray[i]<<endl;
   }
}

public class BMalgo {
   // method for full suffix match
   static void computeFullShift(int[] shiftArr, int[] longSuffArr, String patrn) {
      // length of pattern
      int n = patrn.length();
      int i = n;
      int j = n+1;
      longSuffArr[i] = j;
      while(i > 0) {
         // Searching right if (i-1)th and (j-1)th item are not the same
         while(j <= n && patrn.charAt(i-1) != patrn.charAt(j-1)) {
            // to shift pattern from i to j
            if(shiftArr[j] == 0) {
               shiftArr[j] = j-i;
            }
            // Updating long suffix value
            j = longSuffArr[j];
         }
         i--;
         j--;
         longSuffArr[i] = j;
      }
   }
   // method for good suffix match
   static void computeGoodSuffix(int[] shiftArr, int[] longSuffArr, String patrn) {
      // length of the pattern
      int n = patrn.length();
      int j;
      j = longSuffArr[0];
      // Looping through the pattern
      for(int i = 0; i<n; i++) {
         // setting shift to long suffix value
         if(shiftArr[i] == 0) {
            shiftArr[i] = j;
            if(i == j) {
               // Updating long suffix value
               j = longSuffArr[j];
            }
         }
      }
   }
   // method for searching the pattern
   static void searchPattern(String orgnStr, String patrn, int[] array, int[] index) {
      // length of the pattern
      int patLen = patrn.length();
      // length of main string
      int strLen = orgnStr.length();
      int[] longerSuffArray = new int[patLen+1];
      int[] shiftArr = new int[patLen + 1];
      // Initializing shift array elements to 0
      for(int i = 0; i<=patLen; i++) {
         shiftArr[i] = 0;
      }
      // Calling computeFullShift method
      computeFullShift(shiftArr, longerSuffArray, patrn);
      // Calling computeGoodSuffix method
      computeGoodSuffix(shiftArr, longerSuffArray, patrn);
      int shift = 0;
      while(shift <= (strLen - patLen)) {
         int j = patLen - 1;
         // decrement j when pattern and main string character is matching
         while(j >= 0 && patrn.charAt(j) == orgnStr.charAt(shift+j)) {
            j--;
         }
         if(j < 0) {
            index[0]++;
            // to store the position where pattern is found
            array[index[0]] = shift;
            shift += shiftArr[0];
         }else {
            shift += shiftArr[j+1];
         }
      }
   }
   public static void main(String[] args) {
      // original string
      String orgnStr = "AABAAABCEDBABCDDEBC";
      // Pattern to be searched
      String patrn = "ABC";
      // Array to store the positions where pattern is found
      int[] locArray = new int[orgnStr.length()];
      int[] index = {-1};
      // Calling the searchPattern method
      searchPattern(orgnStr, patrn, locArray, index);
      // Printing the positions where pattern is found
      for(int i = 0; i <= index[0]; i++) {
         System.out.println("Pattern found at position: " + locArray[i]);
      }
   }
}

# Function for full suffix match
def compute_full_shift(shift_arr, long_suff_arr, patrn):
    # length of pattern
    n = len(patrn)
    i = n
    j = n+1
    long_suff_arr[i] = j
    while i > 0:
        # Searching right if (i-1)th and (j-1)th item are not the same
        while j <= n and patrn[i-1] != patrn[j-1]:
            # to shift pattern from i to j
            if shift_arr[j] == 0:
                shift_arr[j] = j-i
            # Updating long suffix value
            j = long_suff_arr[j]
        i -= 1
        j -= 1
        long_suff_arr[i] = j
# Function for good suffix match
def compute_good_suffix(shift_arr, long_suff_arr, patrn):
    # length of the pattern
    n = len(patrn)
    j = long_suff_arr[0]
    # Looping through the pattern
    for i in range(n):
        # setting shift to long suffix value
        if shift_arr[i] == 0:
            shift_arr[i] = j
            if i == j:
                # Updating long suffix value
                j = long_suff_arr[j]

# Function for searching the pattern
def search_pattern(orgn_str, patrn, array, index):
    # length of the pattern
    pat_len = len(patrn)
    # length of main string
    str_len = len(orgn_str)
    longer_suff_array = [0]*(pat_len+1)
    shift_arr = [0]*(pat_len + 1)
    # Initializing shift array elements to 0
    for i in range(pat_len+1):
        shift_arr[i] = 0
    # Calling compute_full_shift function
    compute_full_shift(shift_arr, longer_suff_array, patrn)
    # Calling compute_good_suffix function
    compute_good_suffix(shift_arr, longer_suff_array, patrn)
    shift = 0
    while shift <= (str_len - pat_len):
        j = pat_len - 1
        # decrement j when pattern and main string character is matching
        while j >= 0 and patrn[j] == orgn_str[shift+j]:
            j -= 1
        if j < 0:
            index[0] += 1
            # to store the position where pattern is found
            array[index[0]] = shift
            shift += shift_arr[0]
        else:
            shift += shift_arr[j+1]

# original string
orgn_str = "AABAAABCEDBABCDDEBC"
# Pattern to be searched
patrn = "ABC"
# Array to store the positions where pattern is found
loc_array = [0]*len(orgn_str)
index = [-1]
# Calling the search_pattern function
search_pattern(orgn_str, patrn, loc_array, index)
# Printing the positions where pattern is found
for i in range(index[0]+1):
    print("Pattern found at position: ", loc_array[i])

輸出

Pattern found at position: 5
Pattern found at position: 11
列印頁面
上一頁
下一頁
廣告
© . All rights reserved.