M著色問題

上一頁
下一頁

什麼是M著色問題？

在M著色問題中，我們的任務是確定是否可以為給定圖的節點分配m種不同的顏色，使得圖中沒有兩個相鄰的頂點具有相同的顏色。如果存在解決方案，則顯示每個頂點分配了哪種顏色。M著色問題實際上用於解決諸如聚類、排程、作業分配等問題。

圖是一種抽象資料型別（ADT），由一組透過連結連線的物件組成。

輸入輸出場景

假設給定的無向圖G(V, E)及其鄰接矩陣如下所示：

M-Coloring

設最大顏色m = 3，表示可使用的最大顏色數。回溯演算法可用於解決上述圖的M著色問題。此演算法將返回哪個節點將分配哪個顏色。如果解決方案不可行，則將返回false。

對於這種情況，輸出應為節點0 -> 顏色1，節點1 -> 顏色2，節點2 -> 顏色3，節點3 -> 顏色2。下圖說明了這一點：

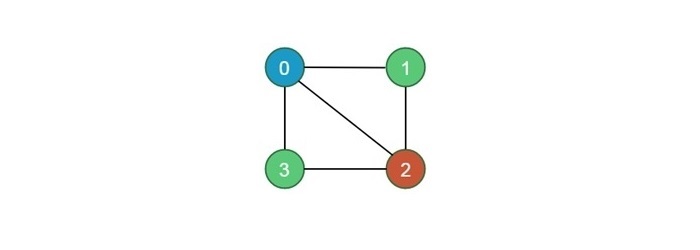
M-Coloring output

使用回溯法解決M著色問題

解決M著色問題的簡單方法是生成所有可能的頂點與顏色組合，並檢查是否有任何組合滿足給定的約束條件。但是，對於較大的圖，這種方法效率低下。

要使用回溯法解決M著色問題，請按照以下步驟操作：

  • 從頂點0開始，我們將嘗試逐個將顏色分配給不同的節點。

  • 但是，在分配之前，我們必須檢查顏色是否安全。當相鄰頂點包含相同的顏色時，顏色不安全。

  • 接下來，我們將檢查是否存在任何滿足約束條件的顏色分配。如果存在，我們將該分配標記為M著色問題的解決方案。

示例

在以下示例中，我們將說明如何在給定的無向圖中解決M著色問題。

C C++ Java Python
#include <stdio.h>
#include <stdlib.h> 
#include <stdbool.h>
#define V 4
bool graph[V][V] = {
   {0, 1, 1, 1},
   {1, 0, 1, 0},
   {1, 1, 0, 1},
   {1, 0, 1, 0}
};
void showColors(int color[]) {
   printf("Assigned Colors are:\n");
   for (int i = 0; i < V; i++)
      printf("%d ", color[i]);
   printf("\n");
}
//check whether putting a color valid for v
bool isValid(int v, int color[], int c) {
   for (int i = 0; i < V; i++)
      if (graph[v][i] && c == color[i])
         return false;
   return true;
}
bool graphColoring(int colors, int color[], int vertex) {
   //when all vertices are considered      
   if (vertex == V)
      return true;
   for (int col = 1; col <= colors; col++) {
      //check whether color is valid or not 
      if (isValid(vertex, color, col)) {
         color[vertex] = col;
         // go for additional vertices
         if (graphColoring(colors, color, vertex + 1))
            return true;
         color[vertex] = 0;
      }
   }
   //when no colors can be assigned
   return false;
}
bool checkSolution(int m) {
   //make color matrix for each vertex   
   int *color = (int *)malloc(V * sizeof(int)); 
   for (int i = 0; i < V; i++)
      //initially set to 0
      color[i] = 0;
   //for vertex 0 check graph coloring      
   if (graphColoring(m, color, 0) == false) {
      printf("Solution does not exist.\n");
      free(color); 
      return false;
   }
   showColors(color);
   free(color); 
   return true;
}

int main() {
   // Number of colors    
   int colors = 3;
   checkSolution(colors);
   return 0;
}

#include<iostream>
#define V 4
using namespace std;
bool graph[V][V] = {
   {0, 1, 1, 1},
   {1, 0, 1, 0},
   {1, 1, 0, 1},
   {1, 0, 1, 0},
};
void showColors(int color[]) {
   cout << "Assigned Colors are: " <<endl;
   for (int i = 0; i < V; i++)
      cout << color[i] << " ";
   cout << endl;
}
//check whether putting a color valid for v
bool isValid(int v,int color[], int c) {    
   for (int i = 0; i < V; i++)
      if (graph[v][i] && c == color[i])
         return false;
   return true;
}
bool graphColoring(int colors, int color[], int vertex) {
   //when all vertices are considered    
   if (vertex == V)    
      return true;
   for (int col = 1; col <= colors; col++) {
      //check whether color is valid or not 
      if (isValid(vertex,color, col)) {     
         color[vertex] = col;
         // go for additional vertices
         if (graphColoring (colors, color, vertex+1) == true)    
            return true;
                   
         color[vertex] = 0;
      }
   }
   //when no colors can be assigned
   return false; 
}
bool checkSolution(int m) {
   //make color matrix for each vertex    
   int *color = new int[V];    
   for (int i = 0; i < V; i++)
      //initially set to 0
      color[i] = 0;      
   //for vertex 0 check graph coloring
   if (graphColoring(m, color, 0) == false) {    
      cout << "Solution does not exist.";
      return false;
   }
   showColors(color);
   return true;
}
int main() {
   // Number of colors    
   int colors = 3;      
   checkSolution (colors);
}

public class GraphColoring {
   static final int V = 4;
   static boolean[][] graph = {
      {false, true, true, true},
      {true, false, true, false},
      {true, true, false, true},
      {true, false, true, false}
   };
   static void showColors(int[] color) {
      System.out.println("Assigned Colors are:");
      for (int i = 0; i < V; i++) {
         System.out.print(color[i] + " ");
      }
      System.out.println();
   }
   //check whether putting a color valid for v
   static boolean isValid(int v, int[] color, int c) {
      for (int i = 0; i < V; i++) {
         if (graph[v][i] && c == color[i]) {
            return false;
         }
      }
      return true;
   }
   static boolean graphColoring(int colors, int[] color, int vertex) {
      //when all vertices are considered    
      if (vertex == V) {
         return true;
      }
      for (int col = 1; col <= colors; col++) {
         //check whether color is valid or not 
         if (isValid(vertex, color, col)) {
            color[vertex] = col;
            // go for additional vertices
            if (graphColoring(colors, color, vertex + 1)) {
               return true;
            }
            color[vertex] = 0;
         }
      }
      //when no colors can be assigned
        return false;
   }
   static boolean checkSolution(int m) {
      //make color matrix for each vertex 
      int[] color = new int[V];
      for (int i = 0; i < V; i++) {
         //initially set to 0
         color[i] = 0;
      }
      //for vertex 0 check graph coloring
      if (!graphColoring(m, color, 0)) {
         System.out.println("Solution does not exist.");
         return false;
      }
      showColors(color);
      return true;
   }
   public static void main(String[] args) {
      // Number of colors 
      int colors = 3;
      checkSolution(colors);
   }
}

V = 4
graph = [
    [0, 1, 1, 1],
    [1, 0, 1, 0],
    [1, 1, 0, 1],
    [1, 0, 1, 0]
]
def show_colors(color):
    print("Assigned Colors are:")
    for i in range(V):
        print(color[i], end=" ")
    print()

def is_valid(v, color, c):
    for i in range(V):
        if graph[v][i] and c == color[i]:
            return False
    return True

def graph_coloring(colors, color, vertex):
    if vertex == V:
        return True
    for col in range(1, colors + 1):
        if is_valid(vertex, color, col):
            color[vertex] = col
            if graph_coloring(colors, color, vertex + 1):
                return True
            color[vertex] = 0
    return False

def check_solution(m):
    color = [0] * V
    if not graph_coloring(m, color, 0):
        print("Solution does not exist.")
        return False
    show_colors(color)
    return True

if __name__ == "__main__":
    colors = 3
    check_solution(colors)

輸出

Assigned Colors are: 
1 2 3 2
列印頁面
上一頁
下一頁
廣告