
- 資料結構與演算法
- DSA - 首頁
- DSA - 概述
- DSA - 環境搭建
- DSA - 演算法基礎
- DSA - 漸近分析
- 資料結構
- DSA - 資料結構基礎
- DSA - 資料結構和型別
- DSA - 陣列資料結構
- 連結串列
- DSA - 連結串列資料結構
- DSA - 雙向連結串列資料結構
- DSA - 迴圈連結串列資料結構
- 棧與佇列
- DSA - 棧資料結構
- DSA - 表示式解析
- DSA - 佇列資料結構
- 搜尋演算法
- DSA - 搜尋演算法
- DSA - 線性查詢演算法
- DSA - 二分查詢演算法
- DSA - 插值搜尋
- DSA - 跳躍搜尋演算法
- DSA - 指數搜尋
- DSA - 斐波那契搜尋
- DSA - 子列表搜尋
- DSA - 雜湊表
- 排序演算法
- DSA - 排序演算法
- DSA - 氣泡排序演算法
- DSA - 插入排序演算法
- DSA - 選擇排序演算法
- DSA - 歸併排序演算法
- DSA - 希爾排序演算法
- DSA - 堆排序
- DSA - 桶排序演算法
- DSA - 計數排序演算法
- DSA - 基數排序演算法
- DSA - 快速排序演算法
- 圖資料結構
- DSA - 圖資料結構
- DSA - 深度優先遍歷
- DSA - 廣度優先遍歷
- DSA - 生成樹
- 樹資料結構
- DSA - 樹資料結構
- DSA - 樹的遍歷
- DSA - 二叉搜尋樹
- DSA - AVL樹
- DSA - 紅黑樹
- DSA - B樹
- DSA - B+樹
- DSA - 伸展樹
- DSA - 字典樹
- DSA - 堆資料結構
- 遞迴
- DSA - 遞迴演算法
- DSA - 使用遞迴實現漢諾塔
- DSA - 使用遞迴實現斐波那契數列
- 分治法
- DSA - 分治法
- DSA - 最大最小問題
- DSA - Strassen矩陣乘法
- DSA - Karatsuba演算法
- 貪心演算法
- DSA - 貪心演算法
- DSA - 旅行商問題(貪心法)
- DSA - Prim最小生成樹
- DSA - Kruskal最小生成樹
- DSA - Dijkstra最短路徑演算法
- DSA - 地圖著色演算法
- DSA - 分數揹包問題
- DSA - 帶截止日期的作業排序
- DSA - 最優合併模式演算法
- 動態規劃
- DSA - 動態規劃
- DSA - 矩陣鏈乘法
- DSA - Floyd-Warshall演算法
- DSA - 0-1揹包問題
- DSA - 最長公共子序列演算法
- DSA - 旅行商問題(動態規劃法)
- 近似演算法
- DSA - 近似演算法
- DSA - 頂點覆蓋演算法
- DSA - 集合覆蓋問題
- DSA - 旅行商問題(近似演算法)
- 隨機化演算法
- DSA - 隨機化演算法
- DSA - 隨機化快速排序演算法
- DSA - Karger最小割演算法
- DSA - Fisher-Yates洗牌演算法
- DSA有用資源
- DSA - 問答
- DSA - 快速指南
- DSA - 有用資源
- DSA - 討論
二分查詢演算法
二分查詢是一種快速搜尋演算法,其執行時間複雜度為O(log n)。這種搜尋演算法基於分治的思想,因為它在搜尋前將陣列分成兩半。為了使該演算法正常工作,資料集合必須已排序。
二分查詢透過比較集合中最中間的專案來查詢特定的鍵值。如果匹配成功,則返回專案的索引。但如果中間項的值大於鍵值,則搜尋中間項的右子陣列。否則,搜尋左子陣列。這個過程遞迴地繼續進行,直到子陣列的大小減小到零。
二分查詢演算法
二分查詢演算法是一種區間搜尋方法,它只在區間內執行搜尋。二分查詢演算法的輸入必須始終是一個已排序的陣列,因為它根據大於或小於的值將陣列劃分為子陣列。演算法遵循以下步驟:
步驟1 - 選擇陣列中的中間項,並將其與要搜尋的鍵值進行比較。如果匹配,則返回中位數的位置。
步驟2 - 如果它與鍵值不匹配,則檢查鍵值是否大於或小於中位數。
步驟3 - 如果鍵值較大,則在右子陣列中執行搜尋;但如果鍵值小於中位數,則在左子陣列中執行搜尋。
步驟4 - 迭代地重複步驟1、2和3,直到子陣列的大小變為1。
步驟5 - 如果鍵值不存在於陣列中,則演算法返回搜尋失敗。
虛擬碼
二分查詢演算法的虛擬碼如下所示:
Procedure binary_search
A ← sorted array
n ← size of array
x ← value to be searched
Set lowerBound = 1
Set upperBound = n
while x not found
if upperBound < lowerBound
EXIT: x does not exists.
set midPoint = lowerBound + ( upperBound - lowerBound ) / 2
if A[midPoint] < x
set lowerBound = midPoint + 1
if A[midPoint] > x
set upperBound = midPoint - 1
if A[midPoint] = x
EXIT: x found at location midPoint
end while
end procedure
分析
由於二分查詢演算法迭代地執行搜尋,因此計算時間複雜度不像線性查詢演算法那樣容易。
輸入陣列透過在每次不成功的迭代後將其劃分為多個子陣列來迭代地搜尋。因此,形成的遞迴關係將是一個除法函式。
簡單來說:
在第一次迭代中,在整個陣列中搜索元素。因此,陣列長度 = n。
在第二次迭代中,只搜尋原始陣列的一半。因此,陣列長度 = n/2。
在第三次迭代中,搜尋前一個子陣列的一半。這裡,陣列長度將為 = n/4。
類似地,在第i次迭代中,陣列長度將變為n/2i
為了實現成功的搜尋,在最後一次迭代後,陣列長度必須為1。因此:
n/2i = 1
這給了我們:
n = 2i
在兩邊應用對數,
log n = log 2i log n = i. log 2 i = log n
二分查詢演算法的時間複雜度為O(log n)
示例
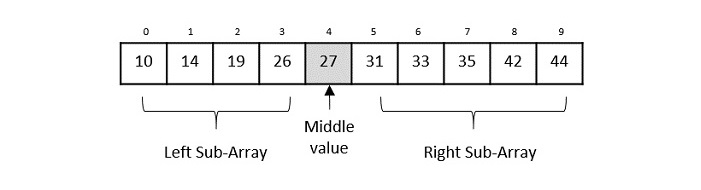
為了使二分查詢工作,目標陣列必須已排序。我們將透過一個圖解示例學習二分查詢的過程。以下是我們的已排序陣列,讓我們假設我們需要使用二分查詢搜尋值31的位置。

首先,我們將使用此公式確定陣列的一半:
mid = low + (high - low) / 2
這裡是:0 + (9 - 0) / 2 = 4(4.5的整數部分)。所以,4是陣列的中點。

現在我們將位置4處儲存的值與要搜尋的值31進行比較。我們發現位置4處的值是27,這並不匹配。由於該值大於27並且我們有一個已排序的陣列,因此我們也知道目標值必須位於陣列的上半部分。

我們將low更改為mid + 1,並再次找到新的mid值。
low = mid + 1 mid = low + (high - low) / 2
我們的新mid現在是7。我們將位置7處儲存的值與我們的目標值31進行比較。
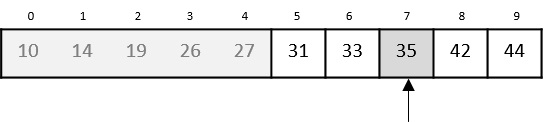
位置7處儲存的值並不匹配,它小於我們正在尋找的值。因此,該值必須位於此位置的下半部分。

因此,我們再次計算mid。這次是5。

我們將位置5處儲存的值與我們的目標值進行比較。我們發現它匹配。

我們得出結論,目標值31儲存在位置5。
二分查詢將可搜尋項減半,從而大大減少了需要進行的比較次數。
實現
二分查詢是一種快速搜尋演算法,其執行時間複雜度為O(log n)。這種搜尋演算法基於分治的思想。為了使該演算法正常工作,資料集合必須已排序。
#include<stdio.h>
void binary_search(int a[], int low, int high, int key){
int mid;
mid = (low + high) / 2;
if (low <= high) {
if (a[mid] == key)
printf("Element found at index: %d\n", mid);
else if(key < a[mid])
binary_search(a, low, mid-1, key);
else if (a[mid] < key)
binary_search(a, mid+1, high, key);
} else if (low > high)
printf("Unsuccessful Search\n");
}
int main(){
int i, n, low, high, key;
n = 5;
low = 0;
high = n-1;
int a[10] = {12, 14, 18, 22, 39};
key = 22;
binary_search(a, low, high, key);
key = 23;
binary_search(a, low, high, key);
return 0;
}
輸出
Element found at index: 3 Unsuccessful Search
#include <iostream>
using namespace std;
void binary_search(int a[], int low, int high, int key){
int mid;
mid = (low + high) / 2;
if (low <= high) {
if (a[mid] == key)
cout << "Element found at index: " << mid << endl;
else if(key < a[mid])
binary_search(a, low, mid-1, key);
else if (a[mid] < key)
binary_search(a, mid+1, high, key);
} else if (low > high)
cout << "Unsuccessful Search" <<endl;
}
int main(){
int i, n, low, high, key;
n = 5;
low = 0;
high = n-1;
int a[10] = {12, 14, 18, 22, 39};
key = 22;
binary_search(a, low, high, key);
key = 23;
binary_search(a, low, high, key);
return 0;
}
輸出
Element found at index: 3 Unsuccessful Search
import java.io.*;
import java.util.*;
public class BinarySearch {
static void binary_search(int a[], int low, int high, int key) {
int mid = (low + high) / 2;
if (low <= high) {
if (a[mid] == key)
System.out.println("Element found at index: " + mid);
else if(key < a[mid])
binary_search(a, low, mid-1, key);
else if (a[mid] < key)
binary_search(a, mid+1, high, key);
} else if (low > high)
System.out.println("Unsuccessful Search");
}
public static void main(String args[]) {
int n, key, low, high;
n = 5;
low = 0;
high = n-1;
int a[] = {12, 14, 18, 22, 39};
key = 22;
binary_search(a, low, high, key);
key = 23;
binary_search(a, low, high, key);
}
}
輸出
Element found at index: 3 Unsuccessful Search
def binary_search(a, low, high, key):
mid = (low + high) // 2
if (low <= high):
if(a[mid] == key):
print("The element is present at index:", mid)
elif(key < a[mid]):
binary_search(a, low, mid-1, key)
elif (a[mid] < key):
binary_search(a, mid+1, high, key)
if(low > high):
print("Unsuccessful Search")
a = [6, 12, 14, 18, 22, 39, 55, 182]
n = len(a)
low = 0
high = n-1
key = 22
binary_search(a, low, high, key)
key = 54
binary_search(a, low, high, key)
輸出
The element is present at index: 4 Unsuccessful Search
