Mahotas - 小波變換

---

---

小波變換是一種將影像分解成不同頻率分量的數學技術。小波變換可以捕捉影像的區域性和全域性細節。

小波變換使用稱為小波的小波形函式來分析訊號。這些小波經過縮放和平移以匹配影像中存在的不同模式。

小波變換涉及修改頻率分量的低頻和高頻係數，以識別模式並增強影像。可以透過小波逆變換恢復原始影像。

讓我們討論一下小波變換技術及其逆變換。

Daubechies變換

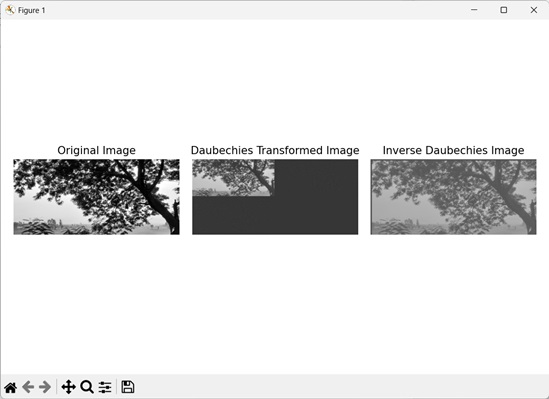
Daubechies變換是一種用於將訊號分解成不同頻率分量的小波變換技術。它允許我們同時在時域和頻域分析訊號。

讓我們看看下面的Daubechies變換影像：

Daubechies逆變換

Daubechies逆變換是Daubechies變換的逆過程。它從透過Daubechies變換獲得的各個頻率分量重建原始影像。

透過應用逆變換，我們可以恢復訊號，同時保留重要的細節。

在這裡，我們來看一下Daubechies逆變換：

Haar變換

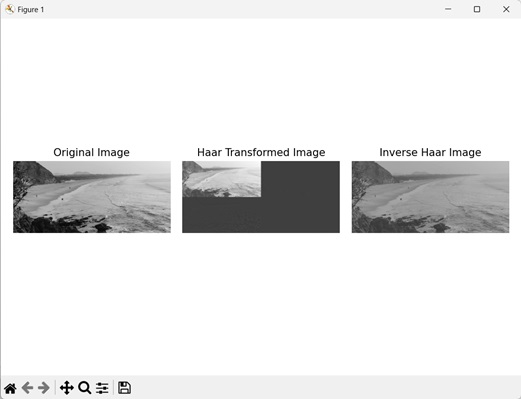
Haar變換技術透過將影像劃分成子區域來將其分解成不同的頻率分量。然後計算平均值之間的差異，以對影像應用小波變換。

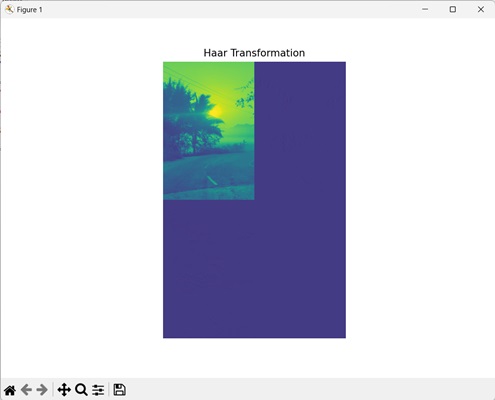
在下圖中，我們看到了Haar變換後的影像：

Haar逆變換

Haar逆變換從透過Haar變換獲得的頻率分量重建原始影像。它是Haar變換的逆運算。

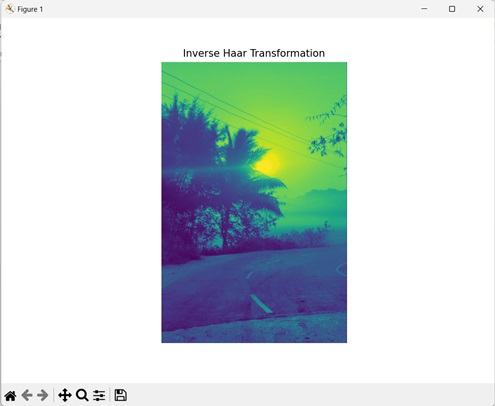
讓我們看一下Haar逆變換：

示例

在下面的示例中，我們嘗試執行上面解釋的所有小波變換：

import mahotas as mh
import numpy as np
import matplotlib.pyplot as mtplt
image = mh.imread('sun.png', as_grey=True)
# Daubechies transformation
daubechies = mh.daubechies(image, 'D6')
mtplt.imshow(daubechies)
mtplt.title('Daubechies Transformation')
mtplt.axis('off')
mtplt.show()
# Inverse Daubechies transformation
daubechies = mh.daubechies(image, 'D6')
inverse_daubechies = mh.idaubechies(daubechies, 'D6')
mtplt.imshow(inverse_daubechies)
mtplt.title('Inverse Daubechies Transformation')
mtplt.axis('off')
mtplt.show()
# Haar transformation
haar = mh.haar(image)
mtplt.imshow(haar)
mtplt.title('Haar Transformation')
mtplt.axis('off')
mtplt.show()
# Inverse Haar transformation
haar = mh.haar(image)
inverse_haar = mh.ihaar(haar)
mtplt.imshow(inverse_haar)
mtplt.title('Inverse Haar Transformation')
mtplt.axis('off')
mtplt.show()

輸出

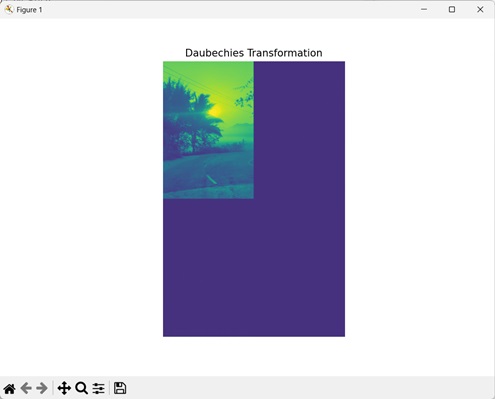
獲得的輸出如下所示：

Daubechies變換

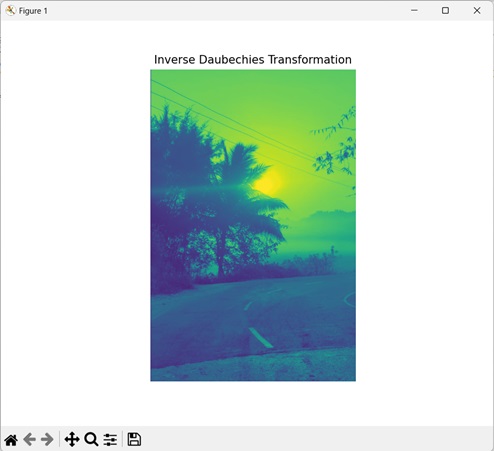
Daubechies逆變換

Haar變換

Haar逆變換

我們將在後面的章節中詳細討論所有的小波變換。