控制系統 - 穩態誤差

---

---

控制系統輸出在穩態下與期望響應的偏差稱為穩態誤差。它表示為$e_{ss}$。我們可以使用終值定理來求解穩態誤差，如下所示。

$$e_{ss}=\lim_{t \to \infty}e(t)=\lim_{s \to 0}sE(s)$$

其中，

E(s)是誤差訊號$e(t)$的拉普拉斯變換

讓我們分別討論如何求解單位反饋和非單位反饋控制系統的穩態誤差。

單位反饋系統的穩態誤差

考慮以下具有單位負反饋的閉環控制系統的框圖。

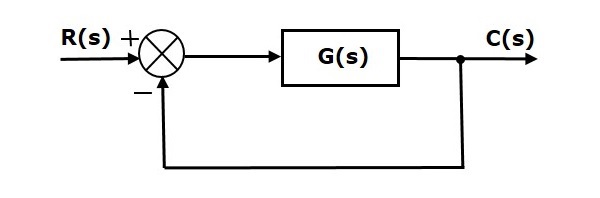
其中，

• R(s)是參考輸入訊號$r(t)$的拉普拉斯變換
• C(s)是輸出訊號$c(t)$的拉普拉斯變換

我們知道單位負反饋閉環控制系統的傳遞函式為

$$\frac{C(s)}{R(s)}=\frac{G(s)}{1+G(s)}$$

$$\Rightarrow C(s)=\frac{R(s)G(s)}{1+G(s)}$$

求和點的輸出為：

$$E(s)=R(s)-C(s)$$

將$C(s)$的值代入上式。

$$E(s)=R(s)-\frac{R(s)G(s)}{1+G(s)}$$

$$\Rightarrow E(s)=\frac{R(s)+R(s)G(s)-R(s)G(s)}{1+G(s)}$$

$$\Rightarrow E(s)=\frac{R(s)}{1+G(s)}$$

將$E(s)$的值代入穩態誤差公式

$$e_{ss}=\lim_{s \to 0} \frac{sR(s)}{1+G(s)}$$

下表顯示了對於單位階躍、單位斜坡和單位拋物線訊號等標準輸入訊號的穩態誤差和誤差常數。

其中，$K_p$、$K_v$和$K_a$分別為位置誤差常數、速度誤差常數和加速度誤差常數。

注意 - 如果上述任何輸入訊號的幅度不為1，則將相應的穩態誤差乘以該幅度。

注意 - 我們無法為單位衝激訊號定義穩態誤差，因為它只存在於原點。因此，我們無法將衝激響應與單位衝激輸入進行比較，因為t表示無窮大。

示例

讓我們求解輸入訊號$r(t)=\left( 5+2t+\frac{t^2}{2} \right )u(t)$的穩態誤差，該訊號具有單位負反饋控制系統，其中$G(s)=\frac{5(s+4)}{s^2(s+1)(s+20)}$

給定的輸入訊號是三個訊號（階躍、斜坡和拋物線）的組合。下表顯示了這三個訊號的誤差常數和穩態誤差值。

我們將透過將上述三個穩態誤差相加來獲得整體穩態誤差。

$$e_{ss}=e_{ss1}+e_{ss2}+e_{ss3}$$

$$\Rightarrow e_{ss}=0+0+1=1$$

因此，在這個例子中，我們得到了穩態誤差$e_{ss}$為1。

非單位反饋系統的穩態誤差

考慮以下具有非單位負反饋的閉環控制系統的框圖。

我們只能為單位反饋系統求解穩態誤差。因此，我們必須將非單位反饋系統轉換為單位反饋系統。為此，在上圖中加入一個單位正反饋路徑和一個單位負反饋路徑。新的框圖如下所示。

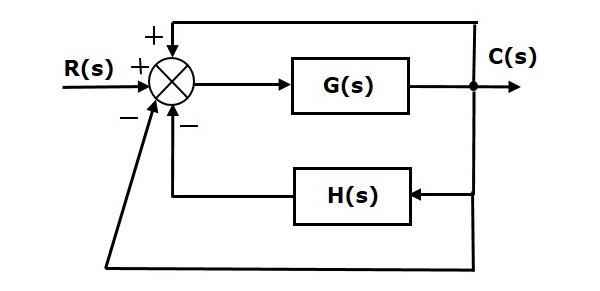
透過保持單位負反饋不變來簡化上圖。簡化後的框圖如下所示。

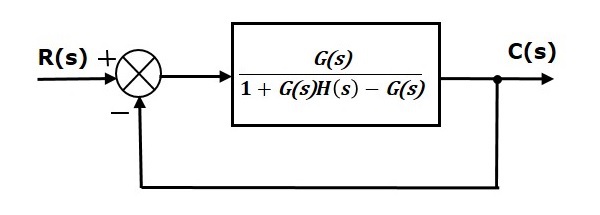
此框圖類似於單位負反饋閉環控制系統的框圖。這裡，單個模組具有傳遞函式$\frac{G(s)}{1+G(s)H(s)-G(s)}$，而不是$G(s)$。您現在可以使用為單位負反饋系統提供的穩態誤差公式來計算穩態誤差。

注意 - 對於不穩定的閉環系統，求解穩態誤差是沒有意義的。因此，我們只需要針對閉環穩定系統計算穩態誤差。這意味著在求解穩態誤差之前，我們需要檢查控制系統是否穩定。在下一章中，我們將討論與穩定性相關的概念。