控制系統 - 訊號流圖

---

---

訊號流圖是代數方程的圖形表示。本章將討論與訊號流圖相關的基本概念，並學習如何繪製訊號流圖。

訊號流圖的基本元素

節點和分支是訊號流圖的基本元素。

節點

節點是一個點，表示變數或訊號。節點有三種類型：輸入節點、輸出節點和混合節點。

• 輸入節點- 只有輸出分支的節點。

• 輸出節點- 只有輸入分支的節點。

• 混合節點- 既有輸入分支也有輸出分支的節點。

示例

讓我們考慮以下訊號流圖來識別這些節點。

• 此訊號流圖中的節點為y₁, y₂, y₃和y₄。

• y₁和y₄分別是輸入節點和輸出節點。

• y₂和y₃是混合節點。

分支

分支是連線兩個節點的線段。它既有增益也有方向。例如，上述訊號流圖中有四個分支。這些分支的增益為a, b, c和-d。

訊號流圖的繪製

讓我們考慮以下代數方程來繪製訊號流圖：

$$y_2=a_{12}y_1+a_{42}y_4$$

$$y_3=a_{23}y_2+a_{53}y_5$$

$$y_4=a_{34}y_3$$

$$y_5=a_{45}y_4+a_{35}y_3$$

$$y_6=a_{56}y_5$$

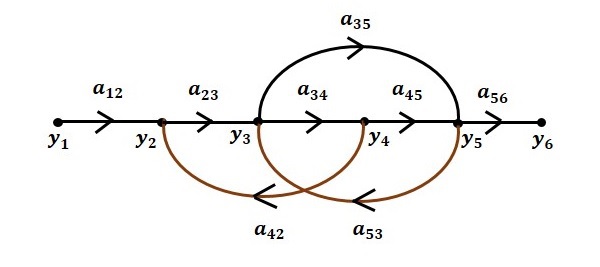
該訊號流圖將有六個節點(y₁, y₂, y₃, y₄, y₅和y₆)和八個分支。分支的增益為a₁₂, a₂₃, a₃₄, a₄₅, a₅₆, a₄₂, a₅₃和a₃₅。

要獲得整體訊號流圖，請為每個方程繪製訊號流圖，然後組合所有這些訊號流圖，然後按照以下步驟操作：

步驟 1 - $y_2 = a_{13}y_1 + a_{42}y_4$ 的訊號流圖如下所示。

步驟 2 - $y_3 = a_{23}y_2 + a_{53}y_5$ 的訊號流圖如下所示。

步驟 3 - $y_4 = a_{34}y_3$ 的訊號流圖如下所示。

步驟 4 - $y_5 = a_{45}y_4 + a_{35}y_3$ 的訊號流圖如下所示。

步驟 5 - $y_6 = a_{56}y_5$ 的訊號流圖如下所示。

步驟 6 - 整體系統的訊號流圖如下所示。

將方塊圖轉換為訊號流圖

按照以下步驟將方塊圖轉換為其等效訊號流圖。

• 將方塊圖的所有訊號、變數、加法點和取樣點表示為訊號流圖中的節點。

• 將方塊圖中的方塊表示為訊號流圖中的分支。

• 將方塊圖中方塊內的傳遞函式表示為訊號流圖中分支的增益。

• 根據方塊圖連線節點。如果兩個節點之間有連線（但中間沒有方塊），則將分支的增益表示為1。例如，加法點之間，加法點和取樣點之間，輸入和加法點之間，取樣點和輸出之間。

示例

讓我們將下面的方塊圖轉換為其等效訊號流圖。

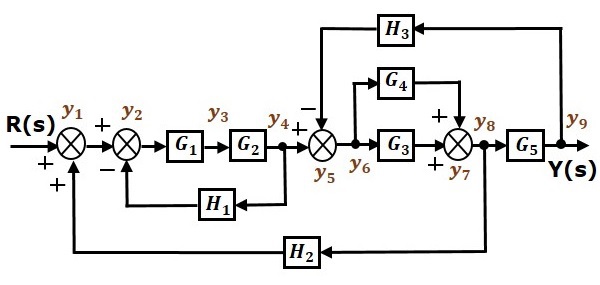
將方塊圖的輸入訊號$R(s)$和輸出訊號$C(s)$表示為訊號流圖的輸入節點$R(s)$和輸出節點$C(s)$。

僅供參考，方塊圖中標註了其餘節點（y₁到y₉）。除了輸入和輸出節點外，還有九個節點。即四個加法點的四個節點，四個取樣點的四個節點，以及$G_1$和$G_2$方塊之間的變數的一個節點。

下圖顯示了等效訊號流圖。

藉助梅森增益公式（下一章討論），您可以計算此訊號流圖的傳遞函式。這是訊號流圖的優勢。在這裡，我們不需要簡化（簡化）訊號流圖來計算傳遞函式。