
- 控制系統教程
- 控制系統 - 首頁
- 控制系統 - 簡介
- 控制系統 - 反饋
- 數學模型
- 機械系統的建模
- 機械系統的電氣等效
- 控制系統 - 方框圖
- 方框圖代數
- 方框圖簡化
- 訊號流圖
- 梅森增益公式
- 時間響應分析
- 一階系統的響應
- 二階系統的響應
- 時域指標
- 穩態誤差
- 控制系統 - 穩定性
- 控制系統 - 穩定性分析
- 控制系統 - 根軌跡
- 根軌跡的繪製
- 頻率響應分析
- 控制系統 - 波特圖
- 波特圖的繪製
- 控制系統 - 極座標圖
- 控制系統 - 奈奎斯特圖
- 控制系統 - 校正器
- 控制系統 - 控制器
- 控制系統 - 狀態空間模型
- 狀態空間分析
- 控制系統有用資源
- 控制系統 - 快速指南
- 控制系統 - 有用資源
- 控制系統 - 討論
控制系統 - 快速指南
控制系統 - 簡介
控制系統是一個透過控制輸出以提供所需響應的系統。下圖顯示了控制系統的簡單方框圖。

在這裡,控制系統由單個方塊表示。由於輸出透過改變輸入來控制,因此控制系統得到了這個名稱。我們將透過某種機制改變這個輸入。在下一節關於開環和閉環控制系統的部分中,我們將詳細研究控制系統內部的方塊以及如何改變此輸入以獲得所需響應。
示例 - 交通訊號燈控制系統,洗衣機
交通訊號燈控制系統是控制系統的一個例子。在這裡,一個輸入訊號序列被應用於此控制系統,輸出是三個燈中的一個,該燈將在一段時間內亮起。在此期間,其他兩個燈將熄滅。根據特定路口的交通研究,可以確定燈的開啟和關閉時間。相應地,輸入訊號控制輸出。因此,交通訊號燈控制系統基於時間執行。
控制系統的分類
基於某些引數,我們可以將控制系統分類如下。
連續時間和離散時間控制系統
根據訊號型別,控制系統可以分為連續時間控制系統和離散時間控制系統。
在連續時間控制系統中,所有訊號都是時間連續的。但是,在離散時間控制系統中,存在一個或多個離散時間訊號。
單輸入單輸出 (SISO) 和多輸入多輸出 (MIMO) 控制系統
根據輸入和輸出的數量,控制系統可以分為單輸入單輸出 (SISO) 控制系統和多輸入多輸出 (MIMO) 控制系統。
單輸入單輸出 (SISO) 控制系統具有一個輸入和一個輸出。而多輸入多輸出 (MIMO) 控制系統則具有多個輸入和多個輸出。
開環和閉環控制系統
根據反饋路徑,控制系統可以分為開環控制系統和閉環控制系統。
在開環控制系統中,輸出不會反饋到輸入。因此,控制作用與所需輸出無關。
下圖顯示了開環控制系統的方框圖。
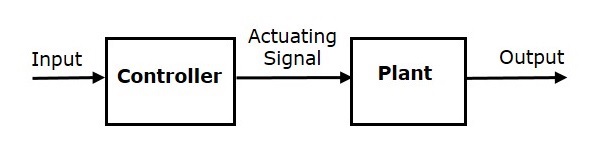
在這裡,輸入被應用於控制器,併產生一個執行訊號或控制訊號。此訊號作為輸入提供給要控制的裝置或過程。因此,裝置產生受控的輸出。我們前面討論的交通訊號燈控制系統就是一個開環控制系統的例子。
在閉環控制系統中,輸出反饋到輸入。因此,控制作用取決於所需輸出。
下圖顯示了負反饋閉環控制系統的方框圖。
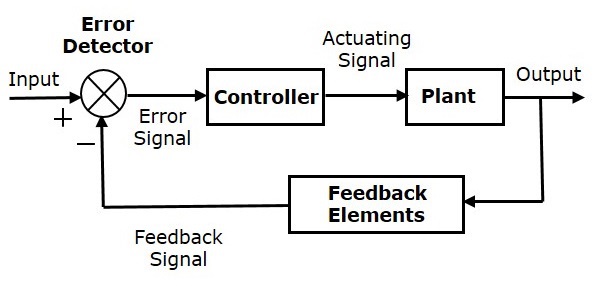
誤差檢測器產生一個誤差訊號,它是輸入和反饋訊號之間的差值。該反饋訊號透過將整個系統的輸出作為此模組的輸入來從模組(反饋元件)中獲得。誤差訊號代替直接輸入作為控制器的輸入。
因此,控制器產生一個控制裝置的執行訊號。在這個組合中,控制系統的輸出會自動調整,直到我們獲得所需的響應。因此,閉環控制系統也稱為自動控制系統。在輸入端帶有感測器的交通訊號燈控制系統就是一個閉環控制系統的例子。
開環和閉環控制系統的區別在下表中列出。
| 開環控制系統 | 閉環控制系統 |
|---|---|
| 控制作用與所需輸出無關。 | 控制作用取決於所需輸出。 |
| 不存在反饋路徑。 | 存在反饋路徑。 |
| 這些也稱為非反饋控制系統。 | 這些也稱為反饋控制系統。 |
| 易於設計。 | 難以設計。 |
| 這些比較經濟。 | 這些成本更高。 |
| 不精確。 | 精確。 |
控制系統 - 反饋
如果輸出或輸出的某些部分返回到輸入端並用作系統輸入的一部分,則稱為反饋。反饋在提高控制系統的效能方面起著重要作用。在本節中,讓我們討論反饋的型別和反饋的影響。
反饋型別
反饋有兩種型別:
- 正反饋
- 負反饋
正反饋
正反饋增加了參考輸入,$R(s)$和反饋輸出。下圖顯示了正反饋控制系統的方框圖。
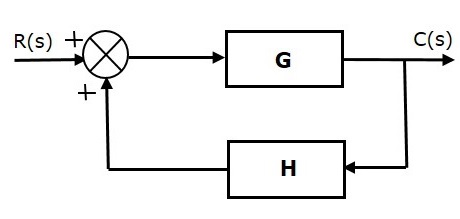
傳遞函式的概念將在後面的章節中討論。目前,考慮正反饋控制系統的傳遞函式為:
$T=\frac{G}{1-GH}$ (公式 1)
其中:
T 是正反饋控制系統的傳遞函式或總增益。
G 是開環增益,它是頻率的函式。
H 是反饋路徑的增益,它是頻率的函式。
負反饋
負反饋減少了參考輸入 $R(s)$ 和系統輸出之間的誤差。下圖顯示了負反饋控制系統的方框圖。

負反饋控制系統的傳遞函式為:
$T=\frac{G}{1+GH}$ (公式 2)
其中:
T 是負反饋控制系統的傳遞函式或總增益。
G 是開環增益,它是頻率的函式。
H 是反饋路徑的增益,它是頻率的函式。
上述傳遞函式的推導在後面的章節中給出。
反饋的影響
現在讓我們瞭解反饋的影響。
反饋對總增益的影響
從公式 2 可以看出,負反饋閉環控制系統的總增益是 'G' 與 (1+GH) 的比值。因此,總增益可能會增加或減少,這取決於 (1+GH) 的值。
如果 (1+GH) 的值小於 1,則總增益增加。在這種情況下,'GH' 值為負,因為反饋路徑的增益為負。
如果 (1+GH) 的值大於 1,則總增益減小。在這種情況下,'GH' 值為正,因為反饋路徑的增益為正。
一般來說,'G' 和 'H' 都是頻率的函式。因此,反饋將在一個頻率範圍內增加系統的總增益,而在另一個頻率範圍內減小。
反饋對靈敏度的影響
負反饋閉環控制系統 (T) 的總增益對開環增益 (G) 變化的靈敏度定義為
$S_{G}^{T} = \frac{\frac{\partial T}{T}}{\frac{\partial G}{G}}=\frac{T的變化百分比}{G的變化百分比}$ (公式 3)
其中,∂T 是由於 G 的增量變化而導致的 T 的增量變化。
我們可以將公式 3 重寫為
$S_{G}^{T}=\frac{\partial T}{\partial G}\frac{G}{T}$ (公式 4)
對公式 2 兩邊關於 G 進行偏微分。
$\frac{\partial T}{\partial G}=\frac{\partial}{\partial G}\left (\frac{G}{1+GH} \right )=\frac{(1+GH).1-G(H)}{(1+GH)^2}=\frac{1}{(1+GH)^2}$ (公式 5)
從公式 2,我們將得到
$\frac{G}{T}=1+GH$ (公式 6)
將公式 5 和公式 6 代入公式 4。
$$S_{G}^{T}=\frac{1}{(1+GH)^2}(1+GH)=\frac{1}{1+GH}$$
因此,我們得到了閉環控制系統的總增益的靈敏度為 (1+GH) 的倒數。因此,靈敏度可能會增加或減少,這取決於 (1+GH) 的值。
如果 (1+GH) 的值小於 1,則靈敏度增加。在這種情況下,'GH' 值為負,因為反饋路徑的增益為負。
如果 (1+GH) 的值大於 1,則靈敏度減小。在這種情況下,'GH' 值為正,因為反饋路徑的增益為正。
一般來說,'G' 和 'H' 都是頻率的函式。因此,反饋將在一個頻率範圍內增加系統增益的靈敏度,而在另一個頻率範圍內減小。因此,我們必須選擇 'GH' 的值,以使系統對引數變化不敏感或不太敏感。
反饋對穩定性的影響
如果系統的輸出處於控制之下,則稱該系統穩定。否則,則稱其不穩定。
在公式 2 中,如果分母值為零(即 GH = -1),則控制系統的輸出將為無限大。因此,控制系統變得不穩定。
因此,我們必須正確選擇反饋以使控制系統穩定。
反饋對噪聲的影響
為了瞭解反饋對噪聲的影響,讓我們比較一下由於噪聲訊號而導致的有反饋和無反饋的傳遞函式關係。
考慮一個如下圖所示的帶有噪聲訊號的開環控制系統。

開環傳遞函式(僅由於噪聲訊號)為
$\frac{C(s)}{N(s)}=G_b$ (公式 7)
這是透過將另一個輸入 $R(s)$ 設定為零獲得的。
考慮一個如下圖所示的帶有噪聲訊號的閉環控制系統。

閉環傳遞函式(僅由於噪聲訊號)為
$\frac{C(s)}{N(s)}=\frac{G_b}{1+G_aG_bH}$ (公式 8)
這是透過將另一個輸入 $R(s)$ 設定為零獲得的。
比較公式 7 和公式 8:
在閉環控制系統中,由於噪聲訊號引起的增益被 $(1+G_a G_b H)$ 因素減小,前提是 $(1+G_a G_b H)$ 大於 1。
控制系統 - 數學模型
控制系統可以用一組稱為數學模型的數學方程來表示。這些模型可用於控制系統的分析和設計。控制系統的分析是指在已知輸入和數學模型的情況下尋找輸出。控制系統的設計是指在已知輸入和輸出的情況下尋找數學模型。
以下數學模型最常用。
- 微分方程模型
- 傳遞函式模型
- 狀態空間模型
本章我們討論前兩種模型。
微分方程模型
微分方程模型是控制系統的時域數學模型。建立微分方程模型,請遵循以下步驟:
將基本定律應用於給定的控制系統。
透過消除中間變數,得到關於輸入和輸出的微分方程。
示例
考慮下圖所示的電路系統。該電路由電阻器、電感器和電容器組成,所有這些元件都串聯連線。施加到該電路的輸入電壓為$v_i$,電容器兩端的電壓為輸出電壓$v_o$。

該電路的網孔方程為:
$$v_i=Ri+L\frac{\text{d}i}{\text{d}t}+v_o$$
將流過電容器的電流$i=c\frac{\text{d}v_o}{\text{d}t}$代入上式。
$$\Rightarrow\:v_i=RC\frac{\text{d}v_o}{\text{d}t}+LC\frac{\text{d}^2v_o}{\text{d}t^2}+v_o$$
$$\Rightarrow\frac{\text{d}^2v_o}{\text{d}t^2}+\left ( \frac{R}{L} \right )\frac{\text{d}v_o}{\text{d}t}+\left ( \frac{1}{LC} \right )v_o=\left ( \frac{1}{LC} \right )v_i$$
上式是一個二階微分方程。
傳遞函式模型
傳遞函式模型是控制系統的s域數學模型。線性時不變 (LTI) 系統的傳遞函式定義為輸出的拉普拉斯變換與輸入的拉普拉斯變換之比,假設所有初始條件均為零。
如果$x(t)$和$y(t)$分別是LTI系統的輸入和輸出,則相應的拉普拉斯變換為$X(s)$和$Y(s)$。
因此,LTI系統的傳遞函式等於$Y(s)$和$X(s)$的比率。
$$即,傳遞函式 =\frac{Y(s)}{X(s)}$$
LTI系統的傳遞函式模型如下圖所示。

在這裡,我們用一個內部包含傳遞函式的方框表示LTI系統。該方框具有輸入$X(s)$和輸出$Y(s)$。
示例
前面我們得到電路系統的微分方程為:
$$\frac{\text{d}^2v_o}{\text{d}t^2}+\left ( \frac{R}{L} \right )\frac{\text{d}v_o}{\text{d}t}+\left ( \frac{1}{LC} \right )v_o=\left ( \frac{1}{LC} \right )v_i$$
對等式兩邊進行拉普拉斯變換。
$$s^2V_o(s)+\left ( \frac{sR}{L} \right )V_o(s)+\left ( \frac{1}{LC} \right )V_o(s)=\left ( \frac{1}{LC} \right )V_i(s)$$
$$\Rightarrow \left \{ s^2+\left ( \frac{R}{L} \right )s+\frac{1}{LC} \right \}V_o(s)=\left ( \frac{1}{LC} \right )V_i(s)$$
$$\Rightarrow \frac{V_o(s)}{V_i(s)}=\frac{\frac{1}{LC}}{s^2+\left ( \frac{R}{L} \right )s+\frac{1}{LC}}$$
其中:
$v_i(s)$是輸入電壓$v_i$的拉普拉斯變換
$v_o(s)$是輸出電壓$v_o$的拉普拉斯變換
上式是二階電路系統的傳遞函式。該系統的傳遞函式模型如下所示。

這裡,我們用一個內部包含傳遞函式的方框表示二階電路系統。該方框具有輸入$V_i(s)$和輸出$V_o(s)$。
機械系統的建模
本章,我們討論機械系統的微分方程建模。根據運動型別,機械系統分為兩種:
- 平動機械系統
- 轉動機械系統
平動機械系統的建模
平動機械系統沿直線運動。這些系統主要由三個基本元件組成:質量、彈簧和阻尼器。
如果對平動機械系統施加力,則會受到由於系統的質量、彈性和摩擦而產生的反作用力的阻礙。由於施加的力和反作用力方向相反,作用在系統上的力的代數和為零。現在讓我們分別看看這三個元件產生的反作用力。
質量
質量是物體的屬性,它儲存動能。如果對質量為M的物體施加力,則會受到由於質量產生的反作用力的阻礙。該反作用力與物體的加速度成正比。假設彈性和摩擦可以忽略不計。
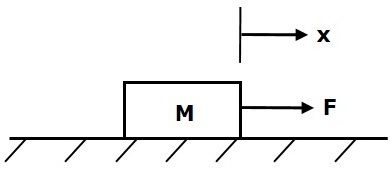
$$F_m\propto\: a$$
$$\Rightarrow F_m=Ma=M\frac{\text{d}^2x}{\text{d}t^2}$$
$$F=F_m=M\frac{\text{d}^2x}{\text{d}t^2}$$
其中:
F為施加的力
Fm為由於質量產生的反作用力
M為質量
a為加速度
x為位移
彈簧
彈簧是一個儲存勢能的元件。如果對彈簧K施加力,則會受到由於彈簧彈性產生的反作用力的阻礙。該反作用力與彈簧的位移成正比。假設質量和摩擦可以忽略不計。
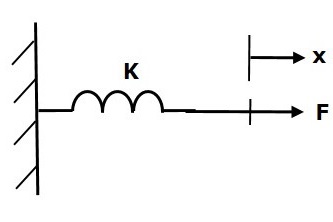
$$F\propto\: x$$
$$\Rightarrow F_k=Kx$$
$$F=F_k=Kx$$
其中:
F為施加的力
Fk為由於彈簧彈性產生的反作用力
K為彈簧常數
x為位移
阻尼器
如果對阻尼器B施加力,則會受到由於阻尼器的摩擦產生的反作用力的阻礙。該反作用力與物體的速度成正比。假設質量和彈性可以忽略不計。
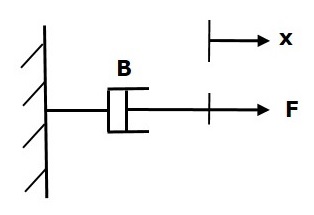
$$F_b\propto\: \nu$$
$$\Rightarrow F_b=B\nu=B\frac{\text{d}x}{\text{d}t}$$
$$F=F_b=B\frac{\text{d}x}{\text{d}t}$$
其中:
Fb為由於阻尼器摩擦產生的反作用力
B為摩擦係數
v為速度
x為位移
轉動機械系統的建模
轉動機械系統繞固定軸旋轉。這些系統主要由三個基本元件組成:轉動慣量、扭轉彈簧和阻尼器。
如果對轉動機械系統施加扭矩,則會受到由於系統的轉動慣量、彈性和摩擦而產生的反作用扭矩的阻礙。由於施加的扭矩和反作用扭矩方向相反,作用在系統上的扭矩的代數和為零。現在讓我們分別看看這三個元件產生的反作用扭矩。
轉動慣量
在平動機械系統中,質量儲存動能。類似地,在轉動機械系統中,轉動慣量儲存動能。
如果對轉動慣量為J的物體施加扭矩,則會受到由於轉動慣量產生的反作用扭矩的阻礙。該反作用扭矩與物體的角加速度成正比。假設彈性和摩擦可以忽略不計。
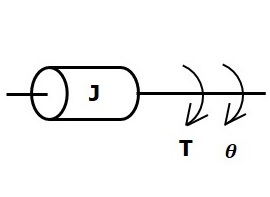
$$T_j\propto\: \alpha$$
$$\Rightarrow T_j=J\alpha=J\frac{\text{d}^2\theta}{\text{d}t^2}$$
$$T=T_j=J\frac{\text{d}^2\theta}{\text{d}t^2}$$
其中:
T為施加的扭矩
Tj為由於轉動慣量產生的反作用扭矩
J為轉動慣量
α為角加速度
θ為角位移
扭轉彈簧
在平動機械系統中,彈簧儲存勢能。類似地,在轉動機械系統中,扭轉彈簧儲存勢能。
如果對扭轉彈簧K施加扭矩,則會受到由於扭轉彈簧彈性產生的反作用扭矩的阻礙。該反作用扭矩與扭轉彈簧的角位移成正比。假設轉動慣量和摩擦可以忽略不計。
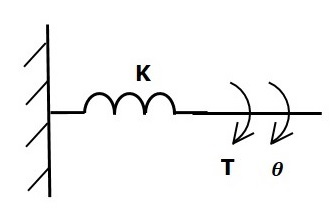
$$T_k\propto\: \theta$$
$$\Rightarrow T_k=K\theta$$
$$T=T_k=K\theta$$
其中:
T為施加的扭矩
Tk為由於扭轉彈簧彈性產生的反作用扭矩
K為扭轉彈簧常數
θ為角位移
阻尼器
如果對阻尼器B施加扭矩,則會受到由於阻尼器的轉動摩擦產生的反作用扭矩的阻礙。該反作用扭矩與物體的角速度成正比。假設轉動慣量和彈性可以忽略不計。

$$T_b\propto\: \omega$$
$$\Rightarrow T_b=B\omega=B\frac{\text{d}\theta}{\text{d}t}$$
$$T=T_b=B\frac{\text{d}\theta}{\text{d}t}$$
其中:
Tb為由於阻尼器的轉動摩擦產生的反作用扭矩
B為轉動摩擦係數
ω為角速度
θ為角位移
機械系統的電氣等效
如果滿足以下兩個條件,則稱兩個系統是類似的。
- 這兩個系統在物理上不同
- 這兩個系統的微分方程建模相同
電路系統和機械系統是兩個物理上不同的系統。平動機械系統有兩種型別的電路模擬:力電壓模擬和力電流模擬。
力電壓模擬
在力電壓模擬中,將平動機械系統的數學方程與電路系統的網孔方程進行比較。
考慮下圖所示的平動機械系統。
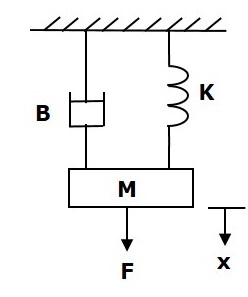
該系統的力平衡方程為:
$$F=F_m+F_b+F_k$$
$\Rightarrow F=M\frac{\text{d}^2x}{\text{d}t^2}+B\frac{\text{d}x}{\text{d}t}+Kx$ (方程 1)
考慮下圖所示的電路系統。該電路由電阻器、電感器和電容器組成,所有這些元件都串聯連線。施加到該電路的輸入電壓為$V$伏特,流過電路的電流為$i$安培。
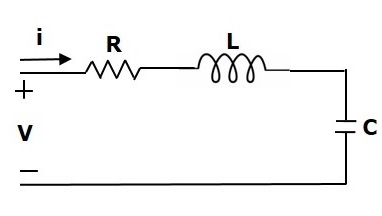
該電路的網孔方程為:
$V=Ri+L\frac{\text{d}i}{\text{d}t}+\frac{1}{c}\int idt$ (方程 2)
將$i=\frac{\text{d}q}{\text{d}t}$代入方程 2。
$$V=R\frac{\text{d}q}{\text{d}t}+L\frac{\text{d}^2q}{\text{d}t^2}+\frac{q}{C}$$
$\Rightarrow V=L\frac{\text{d}^2q}{\text{d}t^2}+R\frac{\text{d}q}{\text{d}t}+\left ( \frac{1}{c} \right )q$ (方程 3)
透過比較方程 1 和方程 3,我們可以得到平動機械系統和電路系統的類似量。下表顯示了這些類似量。
| 平動機械系統 | 電路系統 |
|---|---|
| 力(F) | 電壓(V) |
| 質量(M) | 電感(L) |
| 摩擦係數(B) | 電阻(R) |
| 彈簧常數(K) | 電容的倒數 $(\frac{1}{c})$ |
| 位移(x) | 電荷(q) |
| 速度(v) | 電流(i) |
類似地,轉動機械系統存在扭矩電壓模擬。現在讓我們討論這種模擬。
扭矩電壓模擬
在這種模擬中,將轉動機械系統的數學方程與電路系統的網孔方程進行比較。
轉動機械系統如下圖所示。
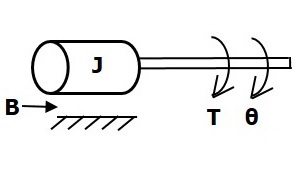
扭矩平衡方程為:
$$T=T_j+T_b+T_k$$
$\Rightarrow T=J\frac{\text{d}^2\theta}{\text{d}t^2}+B\frac{\text{d}\theta}{\text{d}t}+k\theta$ (方程 4)
透過比較方程 4 和方程 3,我們可以得到轉動機械系統和電路系統的類似量。下表顯示了這些類似量。
| 轉動機械系統 | 電路系統 |
|---|---|
| 扭矩(T) | 電壓(V) |
| 轉動慣量(J) | 電感(L) |
| 轉動摩擦係數(B) | 電阻(R) |
| 扭轉彈簧常數(K) | 電容的倒數 $(\frac{1}{c})$ |
| 角位移(θ) | 電荷(q) |
| 角速度(ω) | 電流(i) |
力電流模擬
在力電流模擬中,將平動機械系統的數學方程與電路系統的節點方程進行比較。
考慮下圖所示的電路系統。該電路由電流源、電阻器、電感器和電容器組成,所有這些元件都並聯連線。
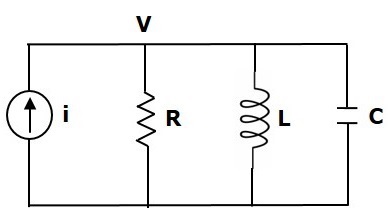
節點方程為:
$i=\frac{V}{R}+\frac{1}{L}\int Vdt+C\frac{\text{d}V}{\text{d}t}$ (方程 5)
將$V=\frac{\text{d}\Psi}{\text{d}t}$代入方程 5。
$$i=\frac{1}{R}\frac{\text{d}\Psi}{\text{d}t}+\left ( \frac{1}{L} \right )\Psi+C\frac{\text{d}^2\Psi}{\text{d}t^2}$$
$\Rightarrow i=C\frac{\text{d}^2\Psi}{\text{d}t^2}+\left ( \frac{1}{R} \right )\frac{\text{d}\Psi}{\text{d}t}+\left ( \frac{1}{L} \right )\Psi$ (方程 6)
透過比較方程 1 和方程 6,我們可以得到平動機械系統和電路系統的類似量。下表顯示了這些類似量。
| 平動機械系統 | 電路系統 |
|---|---|
| 力(F) | 電流(i) |
| 質量(M) | 電容(C) |
| 摩擦係數(B) | 電阻的倒數$(\frac{1}{R})$ |
| 彈簧常數(K) | 電感的倒數$(\frac{1}{L})$ |
| 位移(x) | 磁通量(ψ) |
| 速度(v) | 電壓(V) |
類似地,轉動機械系統存在扭矩電流模擬。現在讓我們討論這種模擬。
扭矩電流模擬
在本例中,旋轉機械系統的數學方程與電路系統的節點網格方程進行了比較。
透過比較公式4和公式6,我們將得到旋轉機械系統和電路系統的相似量。下表顯示了這些相似量。
| 轉動機械系統 | 電路系統 |
|---|---|
| 扭矩(T) | 電流(i) |
| 轉動慣量 (J) | 電容(C) |
| 轉動摩擦係數(B) | 電阻的倒數$(\frac{1}{R})$ |
| 扭轉彈簧常數(K) | 電感的倒數$(\frac{1}{L})$ |
| 角位移 (θ) | 磁通量 (ψ) |
| 角速度 (ω) | 電壓(V) |
本章討論了機械系統的電路模擬。這些模擬有助於從類比電路系統研究和分析非電氣系統,例如機械系統。
控制系統 - 方框圖
框圖由單個方塊或多個方塊組合組成。它們用於以圖形形式表示控制系統。
框圖的基本元素
框圖的基本元素包括方塊、加法點和取樣點。讓我們考慮下圖所示的閉環控制系統的框圖,以識別這些元素。

上圖框圖包含兩個具有傳遞函式G(s)和H(s)的方塊。它還有一個加法點和一個取樣點。箭頭指示訊號流的方向。現在讓我們逐一討論這些元素。
方塊
元件的傳遞函式由一個方塊表示。方塊具有單個輸入和單個輸出。
下圖顯示了一個具有輸入X(s)、輸出Y(s)和傳遞函式G(s)的方塊。

傳遞函式,$G(s)=\frac{Y(s)}{X(s)}$
$$\Rightarrow Y(s)=G(s)X(s)$$
方塊的輸出是透過將方塊的傳遞函式與輸入相乘得到的。
加法點
加法點用內部帶有十字(X)的圓圈表示。它有兩個或多個輸入和單個輸出。它產生輸入的代數和。它還可以根據輸入的極性執行輸入的求和或減法或求和與減法的組合。讓我們逐一看看這三種運算。
下圖顯示了一個具有兩個輸入(A,B)和一個輸出(Y)的加法點。這裡,輸入A和B具有正號。因此,加法點產生輸出Y作為A和B的和。
即,Y = A + B。

下圖顯示了一個具有兩個輸入(A,B)和一個輸出(Y)的加法點。這裡,輸入A和B具有相反的符號,即A具有正號,B具有負號。因此,加法點產生輸出Y作為A和B的差。
Y = A + (-B) = A - B。

下圖顯示了一個具有三個輸入(A,B,C)和一個輸出(Y)的加法點。這裡,輸入A和B具有正號,C具有負號。因此,加法點產生輸出Y為
Y = A + B + (−C) = A + B − C。

取樣點
取樣點是一個點,可以從中將相同的輸入訊號傳遞到多個分支。這意味著藉助取樣點,我們可以將相同的輸入應用於一個或多個方塊、加法點。
在下圖中,取樣點用於將相同的輸入R(s)連線到另外兩個方塊。

在下圖中,取樣點用於將輸出C(s)作為其中一個輸入連線到加法點。

電路系統的框圖表示
在本節中,讓我們用框圖表示一個電路系統。電路系統主要包含三個基本元件——電阻器、電感器和電容器。
考慮下圖所示的RLC串聯電路。其中,Vi(t)和Vo(t)分別是輸入電壓和輸出電壓。設i(t)為流過電路的電流。該電路處於時域。
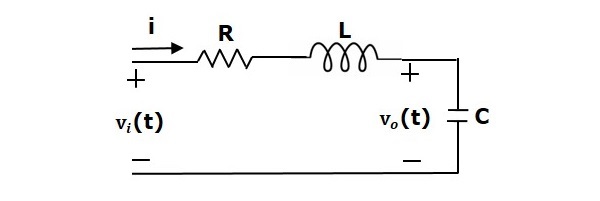
透過對該電路應用拉普拉斯變換,將得到s域中的電路。電路如下圖所示。
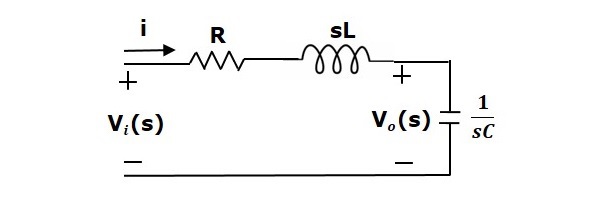
從上圖電路,我們可以寫出
$$I(s)=\frac{V_i(s)-V_o(s)}{R+sL}$$
$\Rightarrow I(s)=\left \{ \frac{1}{R+sL} \right \}\left \{ V_i(s)-V_o(s) \right \}$ (公式1)
$V_o(s)=\left ( \frac{1}{sC} \right )I(s)$ (公式2)
現在讓我們分別繪製這兩個方程的框圖。然後正確地組合這些框圖,以獲得RLC串聯電路(s域)的整體框圖。
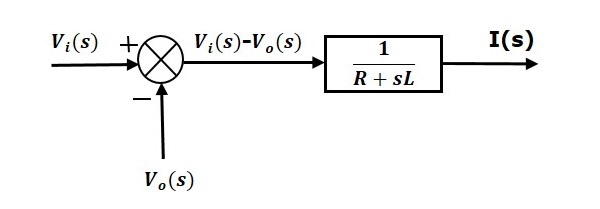
公式1可以用一個具有傳遞函式$\frac{1}{R+sL}$的方塊實現。該方塊的輸入和輸出是$\left \{ V_i(s)-V_o(s) \right \}$和$I(s)$。我們需要一個加法點來獲得$\left \{ V_i(s)-V_o(s) \right \}$。公式1的框圖如下圖所示。
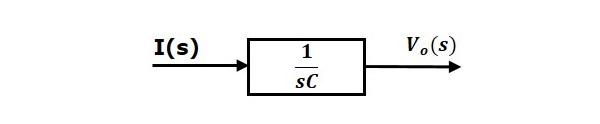
公式2可以用一個具有傳遞函式$\frac{1}{sC}$的方塊實現。該方塊的輸入和輸出是$I(s)$和$V_o(s)$。公式2的框圖如下圖所示。
RLC串聯電路(s域)的整體框圖如下圖所示。

同樣,您可以透過遵循此簡單的步驟來繪製任何電路或系統的框圖。
透過應用拉普拉斯變換將時域電路轉換為s域電路。
寫下流過所有串聯支路元件的電流和所有並聯支路的電壓的方程。
分別繪製所有上述方程的框圖。
正確地組合所有這些框圖,以獲得電路(s域)的整體框圖。
控制系統 - 框圖代數
框圖代數只不過是框圖基本元素所涉及的代數。這種代數處理代數方程的圖形表示。
方塊的基本連線
兩個方塊之間有三種基本型別的連線。
串聯連線
串聯連線也稱為級聯連線。在下圖中,兩個具有傳遞函式$G_1(s)$和$G_2(s)$的方塊串聯連線。

對於這種組合,我們將得到輸出$Y(s)$為
$$Y(s)=G_2(s)Z(s)$$
其中,$Z(s)=G_1(s)X(s)$
$$\Rightarrow Y(s)=G_2(s)[G_1(s)X(s)]=G_1(s)G_2(s)X(s)$$
$$\Rightarrow Y(s)=\lbrace G_1(s)G_2(s)\rbrace X(s)$$
將此方程與輸出方程的標準形式$Y(s)=G(s)X(s)$進行比較。其中,$G(s) = G_1(s)G_2(s)$。
這意味著我們可以用一個方塊表示兩個方塊的串聯連線。該單個方塊的傳遞函式是這兩個方塊的傳遞函式的乘積。等效框圖如下所示。

同樣,您可以用一個方塊表示“n”個方塊的串聯連線。該單個方塊的傳遞函式是所有這些“n”個方塊的傳遞函式的乘積。
並聯連線
並聯連線的方塊將具有相同的輸入。在下圖中,兩個具有傳遞函式$G_1(s)$和$G_2(s)$的方塊並聯連線。這兩個方塊的輸出連線到加法點。

對於這種組合,我們將得到輸出$Y(s)$為
$$Y(s)=Y_1(s)+Y_2(s)$$
其中,$Y_1(s)=G_1(s)X(s)$和$Y_2(s)=G_2(s)X(s)$
$$\Rightarrow Y(s)=G_1(s)X(s)+G_2(s)X(s)=\lbrace G_1(s)+G_2(s)\rbrace X(s)$$
將此方程與輸出方程的標準形式$Y(s)=G(s)X(s)$進行比較。
其中,$G(s)=G_1(s)+G_2(s)$。
這意味著我們可以用一個方塊表示兩個方塊的並聯連線。該單個方塊的傳遞函式是這兩個方塊的傳遞函式的和。等效框圖如下所示。

同樣,您可以用一個方塊表示“n”個方塊的並聯連線。該單個方塊的傳遞函式是所有這些“n”個方塊的傳遞函式的代數和。
反饋連線
正如我們在前幾章中討論的那樣,有兩種型別的反饋——正反饋和負反饋。下圖顯示了負反饋控制系統。這裡,兩個具有傳遞函式$G(s)$和$H(s)$的方塊形成一個閉環。

加法點的輸出為:
$$E(s)=X(s)-H(s)Y(s)$$
輸出$Y(s)$為:
$$Y(s)=E(s)G(s)$$
將$E(s)$的值代入上式。
$$Y(s)=\left \{ X(s)-H(s)Y(s)\rbrace G(s) \right\}$$
$$Y(s)\left \{ 1+G(s)H(s)\rbrace = X(s)G(s) \right\}$$
$$\Rightarrow \frac{Y(s)}{X(s)}=\frac{G(s)}{1+G(s)H(s)}$$
因此,負反饋閉環傳遞函式為$\frac{G(s)}{1+G(s)H(s)}$
這意味著我們可以用一個方塊表示兩個方塊的負反饋連線。該單個方塊的傳遞函式是負反饋的閉環傳遞函式。等效框圖如下所示。

同樣,您可以用一個方塊表示兩個方塊的正反饋連線。該單個方塊的傳遞函式是正反饋的閉環傳遞函式,即$\frac{G(s)}{1-G(s)H(s)}$
加法點的框圖代數
關於方塊,有兩種移動加法點的可能性:
- 將加法點移到方塊之後
- 將加法點移到方塊之前
現在讓我們看看在上述兩種情況下需要進行什麼樣的安排。
將加法點移到方塊之後
考慮下圖所示的框圖。這裡,加法點位於方塊之前。
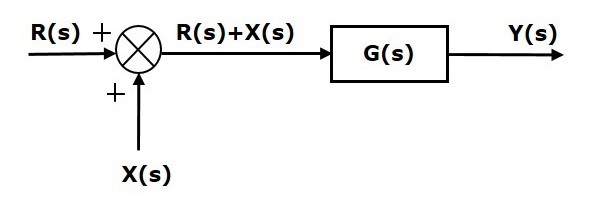
加法點有兩個輸入$R(s)$和$X(s)$。它的輸出是$\left \{R(s)+X(s)\right\}$。
因此,方塊$G(s)$的輸入是$\left \{R(s)+X(s)\right\}$,它的輸出是:
$$Y(s)=G(s)\left \{R(s)+X(s)\right \}$$
$\Rightarrow Y(s)=G(s)R(s)+G(s)X(s)$ (公式1)
現在,將加法點移到方塊之後。該框圖如下圖所示。

方塊$G(s)$的輸出為$G(s)R(s)$。
加法點的輸出為
$Y(s)=G(s)R(s)+X(s)$ (公式2)
比較公式1和公式2。
第一項$‘G(s) R(s)’$在兩個方程中相同。但是,第二項有所不同。為了使第二項也相同,我們需要另一個方塊$G(s)$。它具有輸入$X(s)$,並且該方塊的輸出作為輸入提供給加法點,而不是$X(s)$。該框圖如下圖所示。

將加法點移到方塊之前
考慮下圖所示的框圖。這裡,加法點位於方塊之後。

該框圖的輸出為:
$Y(s)=G(s)R(s)+X(s)$ (公式3)
現在,將加法點移到方塊之前。該框圖如下圖所示。

該框圖的輸出為:
$Y(S)=G(s)R(s)+G(s)X(s)$ (公式4)
比較公式3和公式4,
第一項$‘G(s) R(s)’$在兩個方程中相同。但是,第二項有所不同。為了使第二項也相同,我們需要另一個方塊$\frac{1}{G(s)}$。它具有輸入$X(s)$,並且該方塊的輸出作為輸入提供給加法點,而不是$X(s)$。該框圖如下圖所示。

取樣點的框圖代數
關於方塊,有兩種移動取樣點的可能性:
- 將取樣點移到方塊之後
- 將取樣點移到方塊之前
現在讓我們看看在上述兩種情況下需要進行什麼樣的安排。
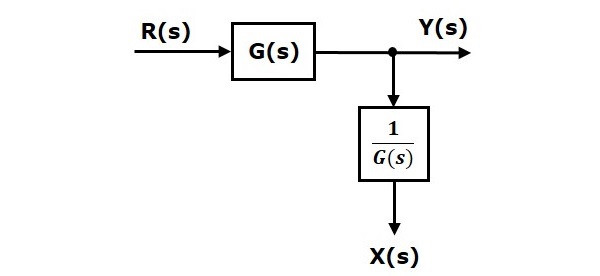
將取樣點移到方塊之後
考慮下圖所示的框圖。在這種情況下,取樣點位於方塊之前。

這裡,$X(s)=R(s)$和$Y(s)=G(s)R(s)$
當您在方塊之後移動取樣點時,輸出 $Y(s)$ 將保持不變。但是,$X(s)$ 的值會發生變化。因此,為了得到相同的 $X(s)$ 值,我們需要另一個方塊 $\frac{1}{G(s)}$。它的輸入為 $Y(s)$,輸出為 $X(s)$。該框圖如下所示。
在方塊之前移動取樣點
考慮下圖所示的框圖。此處,取樣點位於方塊之後。

這裡,$X(s)=Y(s)=G(s)R(s)$
當您在方塊之前移動取樣點時,輸出 $Y(s)$ 將保持不變。但是,$X(s)$ 的值會發生變化。因此,為了得到相同的 $X(s)$ 值,我們需要另一個方塊 $G(s)$。它的輸入為 $R(s)$,輸出為 $X(s)$。該框圖如下所示。

控制系統 - 框圖化簡
前幾章中討論的概念有助於化簡(簡化)框圖。
框圖化簡規則
遵循以下規則來簡化(化簡)包含許多方塊、加法點和取樣點的框圖。
規則 1 − 檢查串聯連線的方塊並進行簡化。
規則 2 − 檢查並聯連線的方塊並進行簡化。
規則 3 − 檢查反饋環路中連線的方塊並進行簡化。
規則 4 − 如果在簡化過程中取樣點存在困難,則將其向右移動。
規則 5 − 如果在簡化過程中加法點存在困難,則將其向左移動。
規則 6 − 重複上述步驟,直到得到簡化形式,即單個方塊。
注意 − 此單個方塊中存在的傳遞函式是整個框圖的傳遞函式。
示例
考慮下圖所示的框圖。讓我們使用框圖化簡規則來簡化(化簡)此框圖。

步驟 1 − 對方塊 $G_1$ 和 $G_2$ 使用規則 1。對方塊 $G_3$ 和 $G_4$ 使用規則 2。修改後的框圖如下所示。

步驟 2 − 對方塊 $G_1G_2$ 和 $H_1$ 使用規則 3。對方塊 $G_5$ 之後移動取樣點使用規則 4。修改後的框圖如下所示。

步驟 3 − 對方塊 $(G_3 + G_4)$ 和 $G_5$ 使用規則 1。修改後的框圖如下所示。

步驟 4 − 對方塊 $(G_3 + G_4)G_5$ 和 $H_3$ 使用規則 3。修改後的框圖如下所示。

步驟 5 − 對串聯連線的方塊使用規則 1。修改後的框圖如下所示。

步驟 6 − 對反饋環路中連線的方塊使用規則 3。修改後的框圖如下所示。這是簡化的框圖。
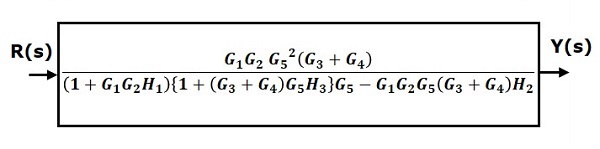
因此,系統的傳遞函式為
$$ \frac{Y(s)}{R(s)} = \frac{G_1G_2G_5^2(G_3+G_4)}{(1+G_1G_2H_1)\{1+(G_3+G_4)G_5H_3\}G_5 - G_1G_2G_5(G_3+G_4)H_2} $$
注意 − 為了計算具有多個輸入的框圖的傳遞函式,請按照以下步驟操作。
步驟 1 − 透過一次考慮一個輸入並將其餘輸入設為零來查詢框圖的傳遞函式。
步驟 2 − 對其餘輸入重複步驟 1。
步驟 3 − 透過新增所有這些傳遞函式來獲得整體傳遞函式。
對於複雜的系統,框圖化簡過程需要更多時間。因為我們必須在每一步之後繪製(部分簡化的)框圖。因此,為了克服這個缺點,可以使用訊號流圖(表示)。
在接下來的兩章中,我們將討論與訊號流圖相關的概念,即如何從給定的框圖表示訊號流圖以及僅使用增益公式而不進行任何化簡過程來計算傳遞函式。
控制系統 - 訊號流圖
訊號流圖是代數方程的圖形表示。在本章中,讓我們討論與訊號流圖相關的基本概念,並學習如何繪製訊號流圖。
訊號流圖的基本元素
節點和分支是訊號流圖的基本元素。
節點
節點是一個點,它表示變數或訊號。共有三種類型的節點——輸入節點、輸出節點和混合節點。
輸入節點 − 它是一個只有輸出分支的節點。
輸出節點 − 它是一個只有輸入分支的節點。
混合節點 − 它是一個同時具有輸入和輸出分支的節點。
示例
讓我們考慮以下訊號流圖來識別這些節點。

此訊號流圖中存在的節點為y1, y2, y3和y4。
y1和y4分別是輸入節點和輸出節點。
y2和y3是混合節點。
分支
分支是連線兩個節點的線段。它同時具有增益和方向。例如,上述訊號流圖中有四個分支。這些分支的增益為a, b, c和-d。
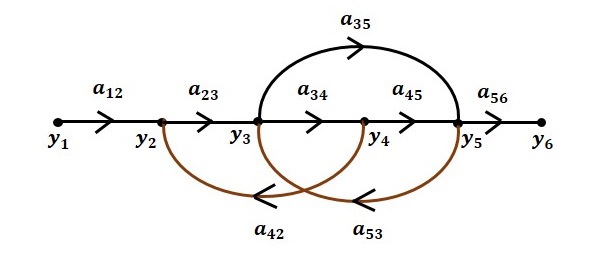
訊號流圖的構造
讓我們透過考慮以下代數方程來構造一個訊號流圖:
$$y_2=a_{12}y_1+a_{42}y_4$$
$$y_3=a_{23}y_2+a_{53}y_5$$
$$y_4=a_{34}y_3$$
$$y_5=a_{45}y_4+a_{35}y_3$$
$$y_6=a_{56}y_5$$
此訊號流圖將有六個節點(y1, y2, y3, y4, y5和y6)和八個分支。分支的增益為a12, a23, a34, a45, a56, a42, a53和a35。
為了獲得整體訊號流圖,請為每個方程繪製訊號流圖,然後組合所有這些訊號流圖,然後按照以下步驟操作:
步驟 1 − $y_2 = a_{13}y_1 + a_{42}y_4$ 的訊號流圖如下所示。

步驟 2 − $y_3 = a_{23}y_2 + a_{53}y_5$ 的訊號流圖如下所示。

步驟 3 − $y_4 = a_{34}y_3$ 的訊號流圖如下所示。

步驟 4 − $y_5 = a_{45}y_4 + a_{35}y_3$ 的訊號流圖如下所示。

步驟 5 − $y_6 = a_{56}y_5$ 的訊號流圖如下所示。

步驟 6 − 整個系統的訊號流圖如下所示。
將框圖轉換為訊號流圖
按照以下步驟將框圖轉換為等效的訊號流圖。
將框圖的所有訊號、變數、加法點和取樣點表示為訊號流圖中的節點。
將框圖的方塊表示為訊號流圖中的分支。
將框圖方塊內的傳遞函式表示為訊號流圖分支的增益。
根據框圖連線節點。如果兩個節點之間存在連線(但兩者之間沒有方塊),則將分支的增益表示為 1。例如,加法點之間、加法點和取樣點之間、輸入和加法點之間、取樣點和輸出之間。
示例
讓我們將以下框圖轉換為其等效的訊號流圖。
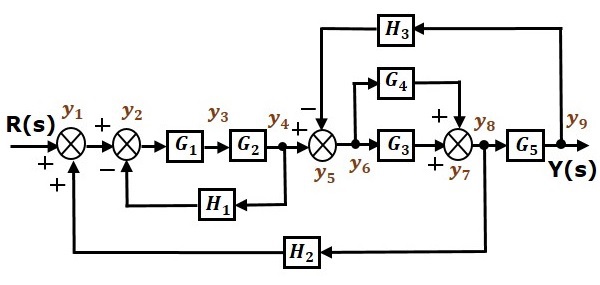
將框圖的輸入訊號 $R(s)$ 和輸出訊號 $C(s)$ 表示為訊號流圖的輸入節點 $R(s)$ 和輸出節點 $C(s)$。
僅供參考,其餘節點 (y1 到 y9) 在框圖中已標記。除了輸入和輸出節點之外,還有九個節點。即四個加法點的四個節點,四個取樣點的四個節點以及方塊 $G_1$ 和 $G_2$ 之間的變數的一個節點。
下圖顯示了等效的訊號流圖。

藉助梅森增益公式(下一章討論),您可以計算此訊號流圖的傳遞函式。這是訊號流圖的優點。在這裡,我們不需要簡化(化簡)訊號流圖來計算傳遞函式。
梅森增益公式
現在讓我們討論梅森增益公式。假設訊號流圖中有“N”個前向路徑。訊號流圖的輸入節點和輸出節點之間的增益就是系統的傳遞函式。可以使用梅森增益公式計算它。
梅森增益公式為
$$T=\frac{C(s)}{R(s)}=\frac{\Sigma ^N _{i=1}P_i\Delta _i}{\Delta}$$
其中:
C(s) 是輸出節點
R(s) 是輸入節點
T 是 $R(s)$ 和 $C(s)$ 之間的傳遞函式或增益
Pi 是第 i 個前向路徑增益
$\Delta =1-(所有單個迴路增益之和)$
$+(所有可能的兩個不相交回路的增益乘積之和)$
$$-(所有可能的三個不相交回路的增益乘積之和)+...$$
透過去除與第 i 個前向路徑相接觸的迴路,可以得到 Δi.
考慮以下訊號流圖,以便理解此處涉及的基本術語。

路徑
它是從一個節點到任何其他節點沿分支箭頭方向的遍歷。它不應遍歷任何節點一次以上。
示例 − $y_2 \rightarrow y_3 \rightarrow y_4 \rightarrow y_5$ 和 $y_5 \rightarrow y_3 \rightarrow y_2$
前向路徑
從輸入節點到輸出節點存在的路徑稱為前向路徑。
示例 − $y_1 \rightarrow y_2 \rightarrow y_3 \rightarrow y_4 \rightarrow y_5 \rightarrow y_6$ 和 $y_1 \rightarrow y_2 \rightarrow y_3 \rightarrow y_5 \rightarrow y_6$。
前向路徑增益
它是透過計算前向路徑的所有分支增益的乘積獲得的。
示例 − $abcde$ 是 $y_1 \rightarrow y_2 \rightarrow y_3 \rightarrow y_4 \rightarrow y_5 \rightarrow y_6$ 的前向通路增益,而 $abge$ 是 $y_1 \rightarrow y_2 \rightarrow y_3 \rightarrow y_5 \rightarrow y_6$ 的前向通路增益。
迴路
從一個節點開始並結束於同一節點的路徑稱為迴路。因此,它是一個閉合路徑。
示例 − $y_2 \rightarrow y_3 \rightarrow y_2$ 和 $y_3 \rightarrow y_5 \rightarrow y_3$。
迴路增益
它是透過計算迴路所有支路增益的乘積獲得的。
示例 − $b_j$ 是 $y_2 \rightarrow y_3 \rightarrow y_2$ 的迴路增益,而 $g_h$ 是 $y_3 \rightarrow y_5 \rightarrow y_3$ 的迴路增益。
不相交回路
這些迴路之間不應有任何公共節點。
示例 − 迴路 $y_2 \rightarrow y_3 \rightarrow y_2$ 和 $y_4 \rightarrow y_5 \rightarrow y_4$ 是不相交的。
使用梅森增益公式計算傳遞函式
讓我們考慮相同的訊號流圖來求傳遞函式。

前向通路數,N = 2。
第一條前向通路為 - $y_1 \rightarrow y_2 \rightarrow y_3 \rightarrow y_4 \rightarrow y_5 \rightarrow y_6$。
第一條前向通路增益,$p_1 = abcde$。
第二條前向通路為 - $y_1 \rightarrow y_2 \rightarrow y_3 \rightarrow y_5 \rightarrow y_6$。
第二條前向通路增益,$p_2 = abge$。
單個迴路數,L = 5。
迴路為 - $y_2 \rightarrow y_3 \rightarrow y_2$,$y_3 \rightarrow y_5 \rightarrow y_3$,$y_3 \rightarrow y_4 \rightarrow y_5 \rightarrow y_3$,$y_4 \rightarrow y_5 \rightarrow y_4$ 和 $y_5 \rightarrow y_5$。
迴路增益為 - $l_1 = bj$,$l_2 = gh$,$l_3 = cdh$,$l_4 = di$ 和 $l_5 = f$。
不相交的兩回路對數 = 2。
第一對不相交回路為 - $y_2 \rightarrow y_3 \rightarrow y_2$,$y_4 \rightarrow y_5 \rightarrow y_4$。
第一對不相交回路的增益乘積,$l_1l_4 = bjdi$
第二對不相交回路為 - $y_2 \rightarrow y_3 \rightarrow y_2$,$y_5 \rightarrow y_5$。
第二對不相交回路的增益乘積為 - $l_1l_5 = bjf$
此訊號流圖中不存在多個(超過兩個)不相交回路。
我們知道,
$\Delta =1-(所有單個迴路增益之和)$
$+(所有可能的兩個不相交回路的增益乘積之和)$
$$-(所有可能的三個不相交回路的增益乘積之和)+...$$
將值代入上式,
$\Delta =1-(bj+gh+cdh+di+f)+(bjdi+bjf)-(0)$
$\Rightarrow \Delta=1-(bj+gh+cdh+di+f)+bjdi+bjf$
沒有與第一條前向通路不相交的迴路。
所以,$\Delta_1=1$。
類似地,$\Delta_2=1$。因為沒有與第二條前向通路不相交的迴路。
將 N = 2 代入梅森增益公式
$$T=\frac{C(s)}{R(s)}=\frac{\Sigma ^2 _{i=1}P_i\Delta _i}{\Delta}$$
$$T=\frac{C(s)}{R(s)}=\frac{P_1\Delta_1+P_2\Delta_2}{\Delta}$$
將所有必要的值代入上式。
$$T=\frac{C(s)}{R(s)}=\frac{(abcde)1+(abge)1}{1-(bj+gh+cdh+di+f)+bjdi+bjf}$$
$$\Rightarrow T=\frac{C(s)}{R(s)}=\frac{(abcde)+(abge)}{1-(bj+gh+cdh+di+f)+bjdi+bjf}$$
因此,傳遞函式為 -
$$T=\frac{C(s)}{R(s)}=\frac{(abcde)+(abge)}{1-(bj+gh+cdh+di+f)+bjdi+bjf}$$
控制系統 - 時間響應分析
我們可以在時域和頻域分析控制系統的響應。我們將在後面的章節中討論控制系統的頻率響應分析。現在讓我們討論控制系統的時間響應分析。
什麼是時間響應?
如果控制系統的輸出對於一個輸入隨時間變化,則稱其為控制系統的時間響應。時間響應包括兩部分。
- 暫態響應
- 穩態響應
下圖顯示了控制系統在時域中的響應。

此處,圖中指出了暫態和穩態。與這些狀態相對應的響應稱為暫態響應和穩態響應。
數學上,我們可以將時間響應 c(t) 寫作
$$c(t)=c_{tr}(t)+c_{ss}(t)$$
其中:
- ctr(t) 是暫態響應
- css(t) 是穩態響應
暫態響應
將輸入施加到控制系統後,輸出需要一定時間才能達到穩態。因此,輸出將處於暫態,直到它進入穩態。因此,控制系統在暫態期間的響應稱為暫態響應。
對於較大的 't' 值,暫態響應將為零。理想情況下,此 't' 值為無窮大,實際上是常數的五倍。
數學上,我們可以寫成
$$\lim_{t\rightarrow \infty }c_{tr}(t)=0$$
穩態響應
即使在暫態響應對於較大的 't' 值為零之後仍然存在的時間響應部分稱為穩態響應。這意味著,即使在穩態期間,暫態響應也將為零。
示例
讓我們找到控制系統 $c(t)=10+5e^{-t}$ 的時間響應的暫態和穩態項。
這裡,第二項 $5e^{-t}$ 將為零,因為 **t** 表示無窮大。所以,這是**暫態項**。而第一項 10 即使當 **t** 趨於無窮大時也仍然存在。所以,這是**穩態項**。
標準測試訊號
標準測試訊號為脈衝、階躍、斜坡和拋物線。這些訊號用於使用輸出的時間響應來了解控制系統的效能。
單位脈衝訊號
單位脈衝訊號 δ(t) 定義為
$\delta (t)=0$ 對於 $t\neq 0$
以及 $\int_{0^-}^{0^+} \delta (t)dt=1$
下圖顯示了單位脈衝訊號。

因此,單位脈衝訊號僅在 't' 等於零時存在。該訊號在圍繞 't' 的較小時間間隔內的面積等於零為一。對於所有其他 't' 值,單位脈衝訊號的值為零。
單位階躍訊號
單位階躍訊號 u(t) 定義為
$$u(t)=1;t\geq 0$$
$=0; t<0$
下圖顯示了單位階躍訊號。

因此,單位階躍訊號存在於所有正 't' 值(包括零)中。在此區間內,其值為 1。對於所有負 't' 值,單位階躍訊號的值為零。
單位斜坡訊號
單位斜坡訊號 r(t) 定義為
$$r(t)=t; t\geq 0$$
$=0; t<0$
我們可以用單位階躍訊號 u(t) 來表示單位斜坡訊號 r(t),如下所示:
$$r(t)=tu(t)$$
下圖顯示了單位斜坡訊號。

因此,單位斜坡訊號存在於所有正 't' 值(包括零)中。在此區間內,其值隨 't' 線性增加。對於所有負 't' 值,單位斜坡訊號的值為零。
單位拋物線訊號
單位拋物線訊號 p(t) 定義為:
$$p(t)=\frac{t^2}{2}; t\geq 0$$
$=0; t<0$
我們可以用單位階躍訊號 u(t) 來表示單位拋物線訊號 p(t),如下所示:
$$p(t)=\frac{t^2}{2}u(t)$$
下圖顯示了單位拋物線訊號。

因此,單位拋物線訊號存在於所有正 **'t'** 值(包括零)中。在此區間內,其值相對於 't' 非線性增加。對於所有負 't' 值,單位拋物線訊號的值為零。
一階系統的響應
在本節中,讓我們討論一階系統的時間響應。考慮以下閉環控制系統的框圖。這裡,一個開環傳遞函式 $\frac{1}{sT}$ 與一個單位負反饋連線。

我們知道,具有單位負反饋的閉環控制系統的傳遞函式為:
$$\frac{C(s)}{R(s)}=\frac{G(s)}{1+G(s)}$$
將 $G(s)=\frac{1}{sT}$ 代入上式。
$$\frac{C(s)}{R(s)}=\frac{\frac{1}{sT}}{1+\frac{1}{sT}}=\frac{1}{sT+1}$$
分母項中 s 的冪為 1。因此,上述傳遞函式是一階的,該系統被稱為一階系統。
我們可以將上述方程改寫為
$$C(s)=\left ( \frac{1}{sT+1} \right )R(s)$$
其中:
C(s) 是輸出訊號 c(t) 的拉普拉斯變換,
R(s) 是輸入訊號 r(t) 的拉普拉斯變換,並且
T 是時間常數。
按照以下步驟獲得時域中一階系統的響應(輸出)。
取輸入訊號 $r(t)$ 的拉普拉斯變換。
考慮方程 $C(s)=\left ( \frac{1}{sT+1} \right )R(s)$
將 $R(s)$ 值代入上式。
如果需要,對 $C(s)$ 進行部分分式分解。
對 $C(s)$ 應用拉普拉斯逆變換。
在上一節中,我們已經看到了標準測試訊號,例如脈衝、階躍、斜坡和拋物線。現在讓我們一一找出每個輸入的一階系統的響應。響應的名稱根據輸入訊號的名稱給出。例如,系統對脈衝輸入的響應稱為脈衝響應。
一階系統的脈衝響應
將單位脈衝訊號作為輸入訊號輸入一階系統。
所以,$r(t)=\delta (t)$
對兩邊應用拉普拉斯變換。
$R(s)=1$
考慮方程 $C(s)=\left ( \frac{1}{sT+1} \right )R(s)$
將 $R(s) = 1$ 代入上式。
$$C(s)=\left ( \frac{1}{sT+1} \right )(1)=\frac{1}{sT+1}$$
將上述方程重新排列成拉普拉斯變換的標準形式之一。
$$C(s)=\frac{1}{T\left (\ s+\frac{1}{T} \right )} \Rightarrow C(s)=\frac{1}{T}\left ( \frac{1}{s+\frac{1}{T}} \right )$$
對兩邊應用拉普拉斯逆變換。
$$c(t)=\frac{1}{T}e^\left ( {-\frac{t}{T}} \right )u(t)$$
下圖顯示了單位脈衝響應。

單位脈衝響應 c(t) 對於正 't' 值是指數衰減訊號,對於負 't' 值則為零。
一階系統的階躍響應
將單位階躍訊號作為輸入訊號輸入一階系統。
所以,$r(t)=u(t)$
對兩邊應用拉普拉斯變換。
$$R(s)=\frac{1}{s}$$
考慮方程 $C(s)=\left ( \frac{1}{sT+1} \right )R(s)$
將 $R(s)=\frac{1}{s}$ 代入上式。
$$C(s)=\left ( \frac{1}{sT+1} \right )\left ( \frac{1}{s} \right )=\frac{1}{s\left ( sT+1 \right )}$$
對 C(s) 進行部分分式分解。
$$C(s)=\frac{1}{s\left ( sT+1 \right )}=\frac{A}{s}+\frac{B}{sT+1}$$
$$\Rightarrow \frac{1}{s\left ( sT+1 \right )}=\frac{A\left ( sT+1 \right )+Bs}{s\left ( sT+1 \right )}$$
在兩邊,分母項是相同的。因此,它們將相互抵消。因此,將分子項相等。
$$1=A\left ( sT+1 \right )+Bs$$
透過將兩邊的常數項相等,您將得到 A = 1。
將 A = 1 代入,並將兩邊的 **s** 係數相等。
$$0=T+B \Rightarrow B=-T$$
將 A = 1 和 B = −T 代入 $C(s)$ 的部分分式展開式中。
$$C(s)=\frac{1}{s}-\frac{T}{sT+1}=\frac{1}{s}-\frac{T}{T\left ( s+\frac{1}{T} \right )}$$
$$\Rightarrow C(s)=\frac{1}{s}-\frac{1}{s+\frac{1}{T}}$$
對兩邊應用拉普拉斯逆變換。
$$c(t)=\left ( 1-e^{-\left ( \frac{t}{T} \right )} \right )u(t)$$
單位階躍響應 c(t) 既有暫態項,也有穩態項。
單位階躍響應中的暫態項為 -
$$c_{tr}(t)=-e^{-\left ( \frac{t}{T} \right )}u(t)$$
單位階躍響應中的穩態項為:
$$c_{ss}(t)=u(t)$$
下圖顯示了單位階躍響應。
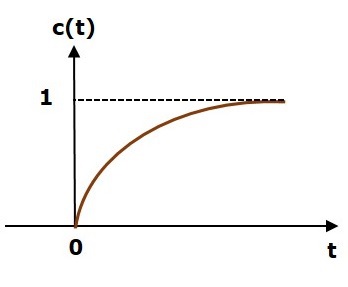
單位階躍響應 c(t) 的值在 t = 0 及所有 t 的負值時均為零。它從零值逐漸增加,最終在穩態時達到一。因此,穩態值取決於輸入的幅度。
一階系統的斜坡響應
考慮將單位斜坡訊號作為輸入訊號輸入到一階系統。
$So, r(t)=tu(t)$
對兩邊應用拉普拉斯變換。
$$R(s)=\frac{1}{s^2}$$
考慮方程 $C(s)=\left ( \frac{1}{sT+1} \right )R(s)$
將 $R(s)=\frac{1}{s^2}$ 代入上式。
$$C(s)=\left ( \frac{1}{sT+1} \right )\left ( \frac{1}{s^2} \right )=\frac{1}{s^2(sT+1)}$$
對 $C(s)$ 進行部分分式分解。
$$C(s)=\frac{1}{s^2(sT+1)}=\frac{A}{s^2}+\frac{B}{s}+\frac{C}{sT+1}$$
$$\Rightarrow \frac{1}{s^2(sT+1)}=\frac{A(sT+1)+Bs(sT+1)+Cs^2}{s^2(sT+1)}$$
在兩邊,分母項是相同的。因此,它們將相互抵消。因此,將分子項相等。
$$1=A(sT+1)+Bs(sT+1)+Cs^2$$
透過將兩邊的常數項相等,您將得到 A = 1。
令 A = 1,並比較兩邊 s 項的係數。
$$0=T+B \Rightarrow B=-T$$
同樣,令 B = −T,並比較兩邊 $s^2$ 項的係數。你將得到 $C=T^2$。
將 A = 1,B = −T 和 $C = T^2$ 代入 $C(s)$ 的部分分式展開式。
$$C(s)=\frac{1}{s^2}-\frac{T}{s}+\frac{T^2}{sT+1}=\frac{1}{s^2}-\frac{T}{s}+\frac{T^2}{T\left ( s+\frac{1}{T} \right )}$$
$$\Rightarrow C(s)=\frac{1}{s^2}-\frac{T}{s}+\frac{T}{s+\frac{1}{T}}$$
對兩邊應用拉普拉斯逆變換。
$$c(t)=\left ( t-T+Te^{-\left ( \frac{t}{T} \right )} \right )u(t)$$
單位斜坡響應 c(t) 包含瞬態項和穩態項。
單位斜坡響應中的瞬態項為:
$$c_{tr}(t)=Te^{-\left ( \frac{t}{T} \right )}u(t)$$
單位斜坡響應中的穩態項為:
$$c_{ss}(t)=(t-T)u(t)$$
下圖顯示了單位斜坡響應。

單位斜坡響應 c(t) 在所有 t 的正值時都遵循單位斜坡輸入訊號。但是,與輸入訊號存在 T 個單位的偏差。
一階系統的拋物線響應
考慮將單位拋物線訊號作為輸入訊號輸入到一階系統。
So, $r(t)=\frac{t^2}{2}u(t)$
對兩邊應用拉普拉斯變換。
$$R(s)=\frac{1}{s^3}$$
考慮方程 $C(s)=\left ( \frac{1}{sT+1} \right )R(s)$
將 $R(s)=\frac{1}{s^3}$ 代入上式。
$$C(s)=\left ( \frac{1}{sT+1} \right )\left( \frac{1}{s^3} \right )=\frac{1}{s^3(sT+1)}$$
對 $C(s)$ 進行部分分式分解。
$$C(s)=\frac{1}{s^3(sT+1)}=\frac{A}{s^3}+\frac{B}{s^2}+\frac{C}{s}+\frac{D}{sT+1}$$
簡化後,你將分別得到 A、B、C 和 D 的值為 1、$-T、\: T^2\: 和 \: −T^3$。將這些值代入上述 $C(s)$ 的部分分式展開式。
$C(s)=\frac{1}{s^3}-\frac{T}{s^2}+\frac{T^2}{s}-\frac{T^3}{sT+1} \: \Rightarrow C(s)=\frac{1}{s^3}-\frac{T}{s^2}+\frac{T^2}{s}-\frac{T^2}{s+\frac{1}{T}}$
對兩邊應用拉普拉斯逆變換。
$$c(t)=\left ( \frac{t^2}{2} -Tt+T^2-T^2e^{-\left ( \frac{t}{T} \right )} \right )u(t)$$
單位拋物線響應 c(t) 包含瞬態項和穩態項。
單位拋物線響應中的瞬態項為
$$C_{tr}(t)=-T^2e^{-\left ( \frac{t}{T} \right )}u(t)$$
單位拋物線響應中的穩態項為
$$C_{ss}(t)=\left ( \frac{t^2}{2} -Tt+T^2 \right )u(t)$$
從這些響應中,我們可以得出結論:對於斜坡和拋物線輸入,一階控制系統不穩定,因為這些響應即使在無限長的時間內也會不斷增加。對於脈衝和階躍輸入,一階控制系統是穩定的,因為這些響應具有有界輸出。但是,脈衝響應沒有穩態項。因此,階躍訊號廣泛用於時域中根據其響應分析控制系統。
二階系統的響應
在本章中,我們將討論二階系統的時域響應。考慮以下閉環控制系統的框圖。這裡,開環傳遞函式 $\frac{\omega ^2_n}{s(s+2\delta \omega_n)}$ 與單位負反饋連線。

我們知道,具有單位負反饋的閉環控制系統的傳遞函式為
$$\frac{C(s)}{R(s)}=\frac{G(s)}{1+G(s)}$$
將 $G(s)=\frac{\omega ^2_n}{s(s+2\delta \omega_n)}$ 代入上式。
$$\frac{C(s)}{R(s)}=\frac{\left (\frac{\omega ^2_n}{s(s+2\delta \omega_n)} \right )}{1+ \left ( \frac{\omega ^2_n}{s(s+2\delta \omega_n)} \right )}=\frac{\omega _n^2}{s^2+2\delta \omega _ns+\omega _n^2}$$
分母項中 's' 的冪為二。因此,上述傳遞函式是二階的,並且該系統被稱為二階系統。
特徵方程為:
$$s^2+2\delta \omega _ns+\omega _n^2=0$$
特徵方程的根為:
$$s=\frac{-2\omega \delta _n\pm \sqrt{(2\delta\omega _n)^2-4\omega _n^2}}{2}=\frac{-2(\delta\omega _n\pm \omega _n\sqrt{\delta ^2-1})}{2}$$
$$\Rightarrow s=-\delta \omega_n \pm \omega _n\sqrt{\delta ^2-1}$$
- 當 δ = 0 時,兩根為虛數。
- 當 δ = 1 時,兩根為實數且相等。
- 當 δ > 1 時,兩根為不相等的實數。
- 當 0 < δ < 1 時,兩根為複共軛數。
我們可以將 $C(s)$ 方程寫為:
$$C(s)=\left ( \frac{\omega _n^2}{s^2+2\delta\omega_ns+\omega_n^2} \right )R(s)$$
其中:
C(s) 是輸出訊號 c(t) 的拉普拉斯變換
R(s) 是輸入訊號 r(t) 的拉普拉斯變換
ωn 是固有頻率
δ 是阻尼比。
按照以下步驟獲得時域中二階系統的響應(輸出)。
對輸入訊號 $r(t)$ 進行拉普拉斯變換。
考慮方程 $C(s)=\left ( \frac{\omega _n^2}{s^2+2\delta\omega_ns+\omega_n^2} \right )R(s)$
將 $R(s)$ 值代入上式。
如果需要,對 $C(s)$ 進行部分分式分解。
對 $C(s)$ 應用拉普拉斯逆變換。
二階系統的階躍響應
考慮將單位階躍訊號作為輸入訊號輸入到二階系統。
單位階躍訊號的拉普拉斯變換為:
$$R(s)=\frac{1}{s}$$
我們知道二階閉環控制系統的傳遞函式為:
$$\frac{C(s)}{R(s)}=\frac{\omega _n^2}{s^2+2\delta\omega_ns+\omega_n^2}$$
情況 1:δ = 0
將 $\delta = 0$ 代入傳遞函式。
$$\frac{C(s)}{R(s)}=\frac{\omega_n^2}{s^2+\omega_n^2}$$
$$\Rightarrow C(s)=\left( \frac{\omega_n^2}{s^2+\omega_n^2} \right )R(s)$$
將 $R(s) = \frac{1}{s}$ 代入上式。
$$C(s)=\left( \frac{\omega_n^2}{s^2+\omega_n^2} \right )\left( \frac{1}{s} \right )=\frac{\omega_n^2}{s(s^2+\omega_n^2)}$$
對兩邊應用拉普拉斯逆變換。
$$c(t)=\left ( 1-\cos(\omega_n t) \right )u(t)$$
因此,當 $/delta = 0$ 時,二階系統的單位階躍響應將是一個具有恆定幅度和頻率的連續時間訊號。
情況 2:δ = 1
將 $/delta = 1$ 代入傳遞函式。
$$\frac{C(s)}{R(s)}=\frac{\omega_n^2}{s^2+2\omega_ns+\omega_n^2}$$
$$\Rightarrow C(s)=\left( \frac{\omega_n^2}{(s+\omega_n)^2} \right)R(s)$$
將 $R(s) = \frac{1}{s}$ 代入上式。
$$C(s)=\left( \frac{\omega_n^2}{(s+\omega_n)^2} \right)\left ( \frac{1}{s} \right)=\frac{\omega_n^2}{s(s+\omega_n)^2}$$
對 $C(s)$ 進行部分分式分解。
$$C(s)=\frac{\omega_n^2}{s(s+\omega_n)^2}=\frac{A}{s}+\frac{B}{s+\omega_n}+\frac{C}{(s+\omega_n)^2}$$
簡化後,你將分別得到 A、B 和 C 的值為 $1,\: -1\: 和 \: −\omega _n$。將這些值代入上述 $C(s)$ 的部分分式展開式。
$$C(s)=\frac{1}{s}-\frac{1}{s+\omega_n}-\frac{\omega_n}{(s+\omega_n)^2}$$
對兩邊應用拉普拉斯逆變換。
$$c(t)=(1-e^{-\omega_nt}-\omega _nte^{-\omega_nt})u(t)$$
因此,二階系統的單位階躍響應將試圖在穩態下達到階躍輸入。
情況 3:0 < δ < 1
我們可以修改傳遞函式的分母項如下:
$$s^2+2\delta\omega_ns+\omega_n^2=\left \{ s^2+2(s)(\delta \omega_n)+(\delta \omega_n)^2 \right \}+\omega_n^2-(\delta\omega_n)^2$$
$$=(s+\delta\omega_n)^2+\omega_n^2(1-\delta^2)$$
傳遞函式變為:
$$\frac{C(s)}{R(s)}=\frac{\omega_n^2}{(s+\delta\omega_n)^2+\omega_n^2(1-\delta^2)}$$
$$\Rightarrow C(s)=\left( \frac{\omega_n^2}{(s+\delta\omega_n)^2+\omega_n^2(1-\delta^2)} \right )R(s)$$
將 $R(s) = \frac{1}{s}$ 代入上式。
$$C(s)=\left( \frac{\omega_n^2}{(s+\delta\omega_n)^2+\omega_n^2(1-\delta^2)} \right )\left( \frac{1}{s} \right )=\frac{\omega_n^2}{s\left ((s+\delta\omega_n)^2+\omega_n^2(1-\delta^2) \right)}$$
對 $C(s)$ 進行部分分式分解。
$$C(s)=\frac{\omega_n^2}{s\left ((s+\delta\omega_n)^2+\omega_n^2(1-\delta^2) \right)}=\frac{A}{s}+\frac{Bs+C}{(s+\delta\omega_n)^2+\omega_n^2(1-\delta^2)}$$
簡化後,你將分別得到 A、B 和 C 的值為 $1,\: -1 \: 和 \: −2\delta \omega _n$。將這些值代入上述 $C(s)$ 的部分分式展開式。
$$C(s)=\frac{1}{s}-\frac{s+2\delta\omega_n}{(s+\delta\omega_n)^2+\omega_n^2(1-\delta^2)}$$
$$C(s)=\frac{1}{s}-\frac{s+\delta\omega_n}{(s+\delta\omega_n)^2+\omega_n^2(1-\delta^2)}-\frac{\delta\omega_n}{(s+\delta\omega_n)^2+\omega_n^2(1-\delta^2)}$$
$C(s)=\frac{1}{s}-\frac{(s+\delta\omega_n)}{(s+\delta\omega_n)^2+(\omega_n\sqrt{1-\delta^2})^2}-\frac{\delta}{\sqrt{1-\delta^2}}\left ( \frac{\omega_n\sqrt{1-\delta^2}}{(s+\delta\omega_n)^2+(\omega_n\sqrt{1-\delta^2})^2} \right )
將 $\omega_n\sqrt{1-\delta^2}$ 作為 $\omega_d$ 代入上式。
$$C(s)=\frac{1}{s}-\frac{(s+\delta\omega_n)}{(s+\delta\omega_n)^2+\omega_d^2}-\frac{\delta}{\sqrt{1-\delta^2}}\left ( \frac{\omega_d}{(s+\delta\omega_n)^2+\omega_d^2} \right )$$
對兩邊應用拉普拉斯逆變換。
$$c(t)=\left ( 1-e^{-\delta \omega_nt}\cos(\omega_dt)-\frac{\delta}{\sqrt{1-\delta^2}}e^{-\delta\omega_nt}\sin(\omega_dt) \right )u(t)$$
$$c(t)=\left ( 1-\frac{e^{-\delta\omega_nt}}{\sqrt{1-\delta^2}}\left ( (\sqrt{1-\delta^2})\cos(\omega_dt)+\delta \sin(\omega_dt) \right ) \right )u(t)$$
如果 $\sqrt{1-\delta^2}=\sin(\theta)$,則 'δ' 將為 cos(θ)。將這些值代入上式。
$$c(t)=\left ( 1-\frac{e^{-\delta\omega_nt}}{\sqrt{1-\delta^2}}(\sin(\theta)\cos(\omega_dt)+\cos(\theta)\sin(\omega_dt)) \right )u(t)$$
$$\Rightarrow c(t)=\left ( 1-\left ( \frac{e^{-\delta\omega_nt}}{\sqrt{1-\delta^2}} \right )\sin(\omega_dt+\theta) \right )u(t)$$
因此,當 'δ' 在零和一之間時,二階系統的單位階躍響應具有阻尼振盪(幅度減小)。
情況 4:δ > 1
我們可以修改傳遞函式的分母項如下:
$$s^2+2\delta\omega_ns+\omega_n^2=\left \{ s^2+2(s)(\delta\omega_n)+(\delta\omega_n)^2 \right \}+\omega_n^2-(\delta\omega_n)^2$$
$$=\left ( s+\delta\omega_n \right )^2-\omega_n^2\left ( \delta^2-1 \right )$$
傳遞函式變為:
$$\frac{C(s)}{R(s)}=\frac{\omega_n^2}{(s+\delta\omega_n)^2-\omega_n^2(\delta^2-1)}$$
$$\Rightarrow C(s)=\left ( \frac{\omega_n^2}{(s+\delta\omega_n)^2-\omega_n^2(\delta^2-1)} \right )R(s)$$
將 $R(s) = \frac{1}{s}$ 代入上式。
$C(s)=\left ( \frac{\omega_n^2}{(s+\delta\omega_n)^2-(\omega_n\sqrt{\delta^2-1})^2} \right )\left ( \frac{1}{s} \right )=\frac{\omega_n^2}{s(s+\delta\omega_n+\omega_n\sqrt{\delta^2-1})(s+\delta\omega_n-\omega_n\sqrt{\delta^2-1})}$
對 $C(s)$ 進行部分分式分解。
$$C(s)=\frac{\omega_n^2}{s(s+\delta\omega_n+\omega_n\sqrt{\delta^2-1})(s+\delta\omega_n-\omega_n\sqrt{\delta^2-1})}$$
$$=\frac{A}{s}+\frac{B}{s+\delta\omega_n+\omega_n\sqrt{\delta^2-1}}+\frac{C}{s+\delta\omega_n-\omega_n\sqrt{\delta^2-1}}$$
簡化後,你將分別得到 A、B 和 C 的值為 1、$\frac{1}{2(\delta+\sqrt{\delta^2-1})(\sqrt{\delta^2-1})}$ 和 $\frac{-1}{2(\delta-\sqrt{\delta^2-1})(\sqrt{\delta^2-1})}$。將這些值代入上述 $C(s)$ 的部分分式展開式。
$$C(s)=\frac{1}{s}+\frac{1}{2(\delta+\sqrt{\delta^2-1})(\sqrt{\delta^2-1})}\left ( \frac{1}{s+\delta\omega_n+\omega_n\sqrt{\delta^2-1}} \right )-\left ( \frac{1}{2(\delta-\sqrt{\delta^2-1})(\sqrt{\delta^2-1})} \right )\left ( \frac{1}{s+\delta\omega_n-\omega_n\sqrt{\delta^2-1}} \right )$$
對兩邊應用拉普拉斯逆變換。
$c(t)=\left ( 1+\left ( \frac{1}{2(\delta+\sqrt{\delta^2-1})(\sqrt{\delta^2-1})} \right )e^{-(\delta\omega_n+\omega_n\sqrt{\delta^2-1})t}-\left ( \frac{1}{2(\delta-\sqrt{\delta^2-1})(\sqrt{\delta^2-1})} \right )e^{-(\delta\omega_n-\omega_n\sqrt{\delta^2-1})t} \right )u(t)$
由於它是過阻尼的,因此當 δ > 1 時,二階系統的單位階躍響應將永遠無法在穩態下達到階躍輸入。
二階系統的脈衝響應
可以使用以下兩種方法之一獲得二階系統的脈衝響應。
在推導階躍響應的過程中,將 $R(s)$ 的值視為 1 而不是 $\frac{1}{s}$,遵循相關的步驟。
對階躍響應進行微分。
下表顯示了對於阻尼比的四種情況,二階系統的脈衝響應。
| 阻尼比條件 | t ≥ 0 時的脈衝響應 |
|---|---|
δ = 0 |
ωnsin(ωnt) |
δ = 1 |
ωn2te-ωnt |
0 < δ < 1 |
(ωne-δωnt/√(1-δ2))sin(ωdt) |
δ > 1 |
(ωn/(2√(δ2-1)))(e-(δωn-ωn√(δ2-1))t - e-(δωn+ωn√(δ2-1))t) |
時域指標
本章討論二階系統的時域指標。下圖顯示了欠阻尼情況下二階系統的階躍響應。

所有時域指標都在此圖中表示。達到穩定時間之前的響應稱為暫態響應,穩定時間之後的響應稱為穩態響應。
延遲時間
它是響應從零時刻達到**最終值的一半**所需的時間。用td表示。
考慮二階系統在t ≥ 0時的階躍響應,其中‘δ’介於零和一之間。
c(t) = 1 - (e-δωnt/√(1-δ2))sin(ωdt+θ)
階躍響應的最終值為1。
因此,在t=td時,階躍響應的值為0.5。將這些值代入上式。
c(td) = 0.5 = 1 - (e-δωntd/√(1-δ2))sin(ωdtd+θ)
=> (e-δωntd/√(1-δ2))sin(ωdtd+θ) = 0.5
使用線性逼近,可以得到**延遲時間td**為
td = (1+0.7δ)/ωn
上升時間
它是響應從**最終值的0%上升到100%**所需的時間。這適用於**欠阻尼系統**。對於過阻尼系統,考慮從最終值的10%到90%的持續時間。上升時間用**tr**表示。
當t = t1 = 0時,c(t) = 0。
我們知道階躍響應的最終值為1。
因此,在t = t2時,階躍響應的值為1。將這些值代入下式。
c(t) = 1 - (e-δωnt/√(1-δ2))sin(ωdt+θ)
c(t2) = 1 = 1 - (e-δωnt2/√(1-δ2))sin(ωdt2+θ)
=> (e-δωnt2/√(1-δ2))sin(ωdt2+θ) = 0
=> sin(ωdt2+θ) = 0
=> ωdt2+θ = π
=> t2 = (π-θ)/ωd
將t1和t2的值代入以下**上升時間**方程:
tr = t2 - t1
∴ tr = (π-θ)/ωd
從上式可以看出,上升時間tr和阻尼頻率ωd成反比。
峰值時間
它是響應第一次達到**峰值**所需的時間。用tp表示。在t = tp時,響應的一階導數為零。
我們知道欠阻尼情況下二階系統的階躍響應為
c(t) = 1 - (e-δωnt/√(1-δ2))sin(ωdt+θ)
對c(t)關於‘t’求導。
dc(t)/dt = -(e-δωnt/√(1-δ2))ωdcos(ωdt+θ) - (-δωne-δωnt/√(1-δ2))sin(ωdt+θ)
將t=tp和dc(t)/dt=0代入上式。
0 = -(e-δωntp/√(1-δ2))[ωdcos(ωdtp+θ)-δωnsin(ωdtp+θ)]
=> ωn√(1-δ2)cos(ωdtp+θ) - δωnsin(ωdtp+θ) = 0
=> √(1-δ2)cos(ωdtp+θ) - δsin(ωdtp+θ) = 0
=> sin(θ)cos(ωdtp+θ) - cos(θ)sin(ωdtp+θ) = 0
=> sin(θ-ωdtp-θ) = 0
=> sin(-ωdtp) = 0 => -sin(ωdtp) = 0 => sin(ωdtp) = 0
=> ωdtp = π
=> tp = π/ωd
從上式可以看出,峰值時間tp和阻尼頻率ωd成反比。
峰值超調
峰值超調**Mp**定義為響應在峰值時間與響應最終值的偏差。也稱為**最大超調**。
數學上,我們可以寫成
Mp = c(tp) - c(∞)
其中:
c(tp)是響應的峰值。
c(∞)是響應的最終值(穩態值)。
在t = tp時,響應c(t)為:
c(tp) = 1 - (e-δωntp/√(1-δ2))sin(ωdtp+θ)
將tp = π/ωd代入上式的右邊。
c(tp) = 1 - (e-δωn(π/ωd)/√(1-δ2))sin(ωd(π/ωd)+θ)
=> c(tp) = 1 - (e-(δπ/√(1-δ2))/√(1-δ2))(-sin(θ))
我們知道
sin(θ) = √(1-δ2)
所以,我們可以得到c(tp)為
c(tp) = 1 + e-(δπ/√(1-δ2))
將c(tp)和c(∞)的值代入峰值超調方程。
Mp = 1 + e-(δπ/√(1-δ2)) - 1
=> Mp = e-(δπ/√(1-δ2))
可以使用此公式計算**峰值超調百分比%**Mp。
%Mp = (Mp/c(∞)) × 100%
將Mp和c(∞)的值代入上式,我們可以得到峰值超調百分比%Mp為
%Mp = (e-(δπ/√(1-δ2))) × 100%
從上式可以看出,如果阻尼比δ增大,峰值超調百分比%Mp將減小。
穩定時間
它是響應達到穩態並保持在最終值周圍指定容差帶內所需的時間。通常,容差帶為2%和5%。穩定時間用ts表示。
5%容差帶的穩定時間為:
ts = 3/(δωn) = 3τ
2%容差帶的穩定時間為:
ts = 4/(δωn) = 4τ
其中,τ是時間常數,等於1/(δωn)。
穩定時間ts和時間常數τ都與阻尼比δ成反比。
穩定時間ts和時間常數τ都與系統增益無關。這意味著即使系統增益發生變化,穩定時間ts和時間常數τ也不會改變。
示例
現在讓我們求出具有閉環傳遞函式4/(s2+2s+4)的控制系統的時域指標,當單位階躍訊號作為輸入訊號施加到該控制系統時。
我們知道二階閉環控制系統的傳遞函式的標準形式為
ωn2/(s2+2δωns+ωn2)
透過將這兩個傳遞函式相等,我們可以得到無阻尼固有頻率ωn為2 rad/sec,阻尼比δ為0.5。
我們知道阻尼頻率ωd的公式為
ωd = ωn√(1-δ2)
將ωn和δ的值代入上式。
=> ωd = 2√(1-(0.5)2)
=> ωd = 1.732 rad/sec
將δ值代入以下關係式
θ = cos-1δ
=> θ = cos-1(0.5) = π/3 rad
將上述必要的值代入每個時域指標的公式中並簡化,以獲得給定傳遞函式的時域指標的值。
下表顯示了時域指標的公式、在公式中代入必要的值以及最終值。
| 時域指標 | 公式 | 在公式中代入的值 | 最終值 |
|---|---|---|---|
延遲時間 |
td = (1+0.7δ)/ωn |
td = (1+0.7(0.5))/2 |
td = 0.675 秒 |
上升時間 |
tr = (π-θ)/ωd |
tr = (π-(π/3))/1.732 |
tr = 1.207 秒 |
峰值時間 |
tp = π/ωd |
tp = π/1.732 |
tp = 1.813 秒 |
峰值超調% |
%Mp = (e-(δπ/√(1-δ2))) × 100% |
%Mp = (e-(0.5π/√(1-(0.5)2))) × 100% |
% Mp = 16.32% |
2%容差帶的穩定時間 |
ts = 4/(δωn) |
ts = 4/((0.5)(2)) |
ts = 4 秒 |
控制系統 - 穩態誤差
控制系統輸出在穩態期間與期望響應的偏差稱為**穩態誤差**。用ess表示。我們可以使用終值定理求出穩態誤差,如下所示。
ess = limt→∞e(t) = lims→0sE(s)
其中:
E(s)是誤差訊號e(t)的拉普拉斯變換。
讓我們逐一討論如何分別求出單位反饋和非單位反饋控制系統的穩態誤差。
單位反饋系統的穩態誤差
考慮以下閉環控制系統的框圖,它具有單位負反饋。
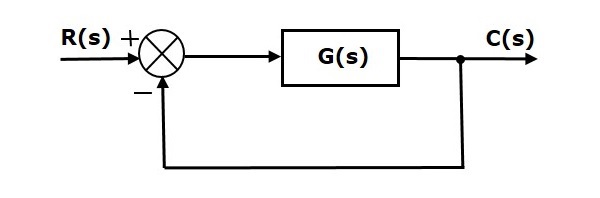
其中:
- R(s)是參考輸入訊號r(t)的拉普拉斯變換
- C(s)是輸出訊號c(t)的拉普拉斯變換
我們知道單位負反饋閉環控制系統的傳遞函式為
$$\frac{C(s)}{R(s)}=\frac{G(s)}{1+G(s)}$$
=> C(s) = R(s)G(s)/(1+G(s))
加法點的輸出為:
E(s) = R(s) - C(s)
將C(s)的值代入上式。
E(s) = R(s) - R(s)G(s)/(1+G(s))
=> E(s) = (R(s) + R(s)G(s) - R(s)G(s))/(1+G(s))
=> E(s) = R(s)/(1+G(s))
將E(s)的值代入穩態誤差公式
ess = lims→0 sR(s)/(1+G(s))
下表顯示了對於單位階躍、單位斜坡和單位拋物線訊號等標準輸入訊號的穩態誤差和誤差常數。
| 輸入訊號 | 穩態誤差ess | 誤差常數 |
|---|---|---|
單位階躍訊號 |
1/(1+kp) |
Kp = lims→0G(s) |
單位斜坡訊號 |
1/Kv |
Kv = lims→0sG(s) |
單位拋物線訊號 |
1/Ka |
Ka = lims→0s2G(s) |
其中,Kp、Kv和Ka分別為位置誤差常數、速度誤差常數和加速度誤差常數。
**注意** - 如果上述任何輸入訊號的幅度不為1,則將相應的穩態誤差乘以該幅度。
**注意** - 我們無法定義單位衝激訊號的穩態誤差,因為它只存在於原點。因此,我們無法將衝激響應與單位衝激輸入進行比較,因為**t**表示無窮大。
示例
讓我們求出具有G(s) = 5(s+4)/(s2(s+1)(s+20))的單位負反饋控制系統的輸入訊號r(t) = (5+2t+t2/2)u(t)的穩態誤差。
給定的輸入訊號是三個訊號(階躍、斜坡和拋物線)的組合。下表顯示了這三個訊號的誤差常數和穩態誤差值。
| 輸入訊號 | 誤差常數 | 穩態誤差 |
|---|---|---|
r1(t) = 5u(t) |
Kp = lims→0G(s) = ∞ |
ess1 = 5/(1+kp) = 0 |
r2(t) = 2tu(t) |
Kv = lims→0sG(s) = ∞ |
ess2 = 2/Kv = 0 |
r3(t) = t2/2u(t) |
Ka = lims→0s2G(s) = 1 |
ess3 = 1/ka = 1 |
透過將上述三個穩態誤差相加,我們可以得到總的穩態誤差。
ess = ess1 + ess2 + ess3
=> ess = 0 + 0 + 1 = 1
因此,對於此示例,我們得到的穩態誤差ess為**1**。
非單位反饋系統的穩態誤差
考慮以下閉環控制系統的框圖,它具有非單位負反饋。

我們只能為單位反饋系統求出穩態誤差。因此,我們必須將非單位反饋系統轉換為單位反饋系統。為此,在上述框圖中新增一個單位正反饋路徑和一個單位負反饋路徑。新的框圖如下所示。
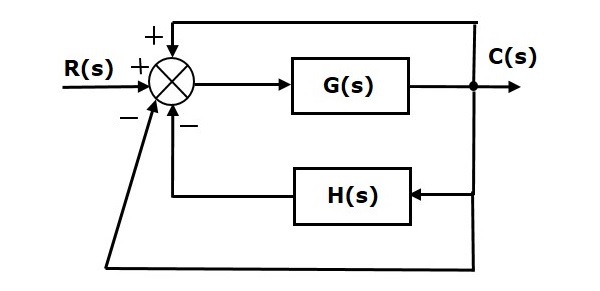
保持單位負反饋不變,簡化上述框圖。簡化後的框圖如下所示。
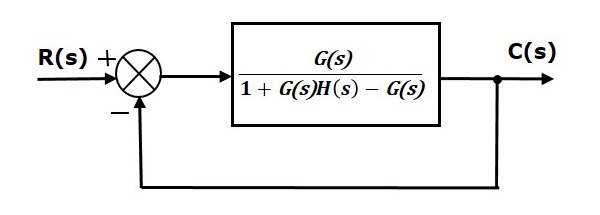
該框圖類似於單位負反饋閉環控制系統的框圖。這裡,單個模組的傳遞函式為$\frac{G(s)}{1+G(s)H(s)-G(s)}$,而不是$G(s)$。現在可以使用單位負反饋系統的穩態誤差公式計算穩態誤差。
注意 − 對不穩定的閉環系統求穩態誤差是沒有意義的。因此,我們只需要計算閉環穩定系統的穩態誤差。這意味著在求穩態誤差之前,我們需要檢查控制系統是否穩定。在下一章中,我們將討論與穩定性相關的概念。
控制系統 - 穩定性
穩定性是一個重要的概念。本章,讓我們討論系統的穩定性和基於穩定性的系統型別。
什麼是穩定性?
如果系統的輸出處於受控狀態,則稱該系統為穩定系統;否則,則稱其為不穩定系統。對於給定的有界輸入,穩定系統產生有界輸出。
下圖顯示了穩定系統的響應。

這是單位階躍輸入的一階控制系統的響應。該響應的值介於0和1之間,因此是有界輸出。我們知道,單位階躍訊號在包括零在內的所有正值t處的值均為1。因此,它是界輸入。因此,由於輸入和輸出都是有界的,所以一階控制系統是穩定的。
基於穩定性的系統型別
我們可以根據穩定性對系統進行如下分類。
- 絕對穩定系統
- 條件穩定系統
- 臨界穩定系統
絕對穩定系統
如果系統在所有系統元件值範圍內都穩定,則稱為絕對穩定系統。如果開環傳遞函式的所有極點都位於‘s’平面的左半平面,則開環控制系統是絕對穩定的。類似地,如果閉環傳遞函式的所有極點都位於‘s’平面的左半平面,則閉環控制系統是絕對穩定的。
條件穩定系統
如果系統在某個系統元件值範圍內穩定,則稱為條件穩定系統。
臨界穩定系統
如果系統透過產生具有恆定幅度和恆定頻率振盪的有界輸出訊號而穩定,則稱為臨界穩定系統。如果開環傳遞函式的任何兩個極點都位於虛軸上,則開環控制系統是臨界穩定的。類似地,如果閉環傳遞函式的任何兩個極點都位於虛軸上,則閉環控制系統是臨界穩定的。
控制系統 - 穩定性分析
本章,讓我們使用Routh-Hurwitz穩定性判據討論‘s’域中的穩定性分析。在這個判據中,我們需要特徵方程來確定閉環控制系統的穩定性。
Routh-Hurwitz穩定性判據
Routh-Hurwitz穩定性判據具有一個穩定性的必要條件和一個充分條件。如果任何控制系統都不滿足必要條件,則可以說該控制系統是不穩定的。但是,如果控制系統滿足必要條件,則它可能穩定也可能不穩定。因此,充分條件有助於確定控制系統是否穩定。
Routh-Hurwitz穩定性的必要條件
必要條件是特徵多項式的係數應為正。這意味著特徵方程的所有根都應具有負實部。
考慮'n'階的特徵方程為:
$$a_0s^n+a_1s^{n-1}+a_2s^{n-2}+...+a_{n-1}s^1+a_ns^0=0$$
注意,nth階特徵方程中不應缺少任何項。這意味著nth階特徵方程不應有任何係數為零。
Routh-Hurwitz穩定性的充分條件
充分條件是Routh表第一列的所有元素都應具有相同的符號。這意味著Routh表第一列的所有元素都應為正或為負。
Routh表法
如果特徵方程的所有根都存在於‘s’平面的左半平面,則控制系統是穩定的。如果特徵方程的至少一個根存在於‘s’平面的右半平面,則控制系統是不穩定的。因此,我們必須找到特徵方程的根才能知道控制系統是穩定的還是不穩定的。但是,隨著階數的增加,找到特徵方程的根變得困難。
因此,為了克服這個問題,我們有Routh表法。在這種方法中,不需要計算特徵方程的根。首先構造Routh表,然後找到Routh表第一列中符號變化的次數。Routh表第一列中符號變化的次數給出了存在於‘s’平面右半平面的特徵方程根的個數,控制系統是不穩定的。
按照此步驟構造Routh表。
用特徵多項式的係數填充Routh表的首兩行,如下表所示。從$s^n$的係數開始,一直到$s^0$的係數。
用下表中提到的元素填充Routh表的其餘行。繼續此過程,直到得到第$s^0$行的第一列元素為$a_n$。這裡,$a_n$是特徵多項式中$s^0$的係數。
注意 − 如果Routh表的任何一行元素具有某些公因子,則可以用該因子除以該行元素,以便簡化。
下表顯示了n階特徵多項式的Routh表。
$$a_0s^n+a_1s^{n-1}+a_2s^{n-2}+...+a_{n-1}s^1+a_ns^0$$
$s^n$ |
$a_0$ |
$a_2$ |
$a_4$ |
$a_6$ |
... |
... |
$s^{n-1}$ |
$a_1$ |
$a_3$ |
$a_5$ |
$a_7$ |
... |
... |
$s^{n-2}$ |
$b_1=\frac{a_1a_2-a_3a_0}{a_1}$ |
$b_2=\frac{a_1a_4-a_5a_0}{a_1}$ |
$b_3=\frac{a_1a_6-a_7a_0}{a_1}$ |
... |
... |
... |
$s^{n-3}$ |
$c_1=\frac{b_1a_3-b_2a_1}{b_1}$ |
$c_2=\frac{b_1a_5-b_3a_1}{b_1}$ |
$\vdots$ |
|||
$\vdots$ |
$\vdots$ |
$\vdots$ |
$\vdots$ |
|||
$s^1$ |
$\vdots$ |
$\vdots$ |
||||
$s^0$ |
$a_n$ |
示例
讓我們找到具有特徵方程的控制系統的穩定性,
$$s^4+3s^3+3s^2+2s+1=0$$
步驟1 − 驗證Routh-Hurwitz穩定性的必要條件。
特徵多項式$s^4+3s^3+3s^2+2s+1$的所有係數都為正。因此,控制系統滿足必要條件。
步驟2 − 為給定的特徵多項式構造Routh表。
$s^4$ |
$1$ |
$3$ |
$1$ |
$1$ |
$3$ |
$2$ |
|
$3$ |
$\frac{(3 \times 3)-(2 \times 1)}{3}=\frac{7}{3}$ |
$\frac{(3 \times 1)-(0 \times 1)}{3}=\frac{3}{3}=1$ |
|
$s^1$ |
$\frac{\left ( \frac{7}{3}\times 2 \right )-(1 \times 3)}{\frac{7}{3}}=\frac{5}{7}$ |
||
$s^0$ |
$1$ |
步驟3 − 驗證Routh-Hurwitz穩定性的充分條件。
Routh表第一列的所有元素都為正。Routh表第一列中沒有符號變化。因此,控制系統是穩定的。
Routh表的特殊情況
在構造Routh表時,我們可能會遇到兩種情況。從這兩種情況中很難完成Routh表。
這兩種特殊情況是:
- Routh表的任何一行的第一個元素為零。
- Routh表的任何一行的所有元素都為零。
讓我們逐一討論如何克服這兩種情況下的困難。
Routh表的任何一行的第一個元素為零
如果Routh表的任何一行只有第一個元素為零,而至少一個剩餘元素的值不為零,則用一個小的正整數$\epsilon$替換第一個元素。然後繼續完成Routh表的步驟。現在,透過將$\epsilon$趨於零來查詢Routh表第一列中符號變化的次數。
示例
讓我們找到具有特徵方程的控制系統的穩定性,
$$s^4+2s^3+s^2+2s+1=0$$
步驟1 − 驗證Routh-Hurwitz穩定性的必要條件。
特徵多項式$s^4+2s^3+s^2+2s+1$的所有係數都為正。因此,控制系統滿足必要條件。
步驟2 − 為給定的特徵多項式構造Routh表。
$s^4$ |
$1$ |
$1$ |
$1$ |
$1$ |
|
|
|
$3$ |
$\frac{(1 \times 1)-(1 \times 1)}{1}=0$ |
$\frac{(1 \times 1)-(0 \times 1)}{1}=1$ |
|
$s^1$ |
|||
$s^0$ |
$s^3$行的元素具有2作為公因子。因此,所有這些元素都除以2。
特殊情況(i) − $s^2$行的只有第一個元素為零。因此,用$\epsilon$替換它,並繼續完成Routh表的步驟。
$s^4$ |
1 |
1 |
1 |
$1$ |
1 |
1 |
|
$3$ |
$\epsilon$ |
1 |
|
$s^1$ |
$\frac{\left ( \epsilon \times 1 \right )-\left ( 1 \times 1 \right )}{\epsilon}=\frac{\epsilon-1}{\epsilon}$ |
||
$s^0$ |
1 |
步驟3 − 驗證Routh-Hurwitz穩定性的充分條件。
當$\epsilon$趨於零時,Routh表如下所示。
$s^4$ |
1 |
1 |
1 |
$1$ |
1 |
1 |
|
$3$ |
0 |
1 |
|
$s^1$ |
-∞ |
||
$s^0$ |
1 |
Routh表的第一列有兩個符號變化。因此,控制系統是不穩定的。
Routh表的任何一行的所有元素都為零
在這種情況下,請遵循以下兩個步驟:
寫出恰好在零行上方的行的輔助方程A(s)。
對方程A(s)關於s求導。用這些係數填充零行。
示例
讓我們找到具有特徵方程的控制系統的穩定性,
$$s^5+3s^4+s^3+3s^2+s+3=0$$
步驟1 − 驗證Routh-Hurwitz穩定性的必要條件。
給定特徵多項式的所有係數都為正。因此,控制系統滿足必要條件。
步驟2 − 為給定的特徵多項式構造Routh表。
$s^5$ |
1 |
1 |
1 |
$s^4$ |
|
|
|
$1$ |
$\frac{(1 \times 1)-(1 \times 1)}{1}=0$ |
$\frac{(1 \times 1)-(1 \times 1)}{1}=0$ |
|
$3$ |
|||
$s^1$ |
|||
$s^0$ |
$s^4$行的元素具有3的公因子。因此,所有這些元素都除以3。
特殊情況(ii) − $s^3$行的所有元素都為零。因此,編寫$s^4$行的輔助方程A(s)。
$$A(s)=s^4+s^2+1$$
對方程關於s求導。
$$\frac{\text{d}A(s)}{\text{d}s}=4s^3+2s$$
將這些係數放在$s^3$行。
$s^5$ |
1 |
1 |
1 |
$s^4$ |
1 |
1 |
1 |
$1$ |
|
|
|
$3$ |
$\frac{(2 \times 1)-(1 \times 1)}{2}=0.5$ |
$\frac{(2 \times 1)-(0 \times 1)}{2}=1$ |
|
$s^1$ |
$\frac{(0.5 \times 1)-(1 \times 2)}{0.5}=\frac{-1.5}{0.5}=-3$ |
||
$s^0$ |
1 |
步驟3 − 驗證Routh-Hurwitz穩定性的充分條件。
Routh表的第一列有兩個符號變化。因此,控制系統是不穩定的。
在Routh-Hurwitz穩定性判據中,我們可以知道閉環極點位於‘s’平面的左半平面、右半平面還是虛軸上。因此,我們無法找到控制系統的性質。為了克服這一限制,有一種稱為根軌跡的技術。我們將在接下來的兩章中討論這種技術。
控制系統 - 根軌跡
在根軌跡圖中,我們可以觀察到閉環極點的路徑。因此,我們可以識別控制系統的性質。在這種技術中,我們將使用開環傳遞函式來了解閉環控制系統的穩定性。
根軌跡的基礎
根軌跡是透過將系統增益K從零變化到無窮大而得到的特徵方程根的軌跡。
我們知道,閉環控制系統的特徵方程是
$$1+G(s)H(s)=0$$
我們可以將$G(s)H(s)$表示為
$$G(s)H(s)=K\frac{N(s)}{D(s)}$$
其中:
K代表乘法因子
N(s)代表具有's'的n階多項式(因式分解)的分子項。
D(s)代表具有's'的m階多項式(因式分解)的分母項。
將$G(s)H(s)$的值代入特徵方程。
$$1+k\frac{N(s)}{D(s)}=0$$
$$\Rightarrow D(s)+KN(s)=0$$
情況1 − K = 0
如果 $K=0$,則 $D(s)=0$。
這意味著,當 K 為零時,閉環極點等於開環極點。
情況 2 − K = ∞
將上述特徵方程改寫為
$$K\left(\frac{1}{K}+\frac{N(s)}{D(s)} \right )=0 \Rightarrow \frac{1}{K}+\frac{N(s)}{D(s)}=0$$
在上述方程中代入 $K = \infty$。
$$\frac{1}{\infty}+\frac{N(s)}{D(s)}=0 \Rightarrow \frac{N(s)}{D(s)}=0 \Rightarrow N(s)=0$$
如果 $K=\infty$,則 $N(s)=0$。這意味著當 K 為無窮大時,閉環極點等於開環零點。
從以上兩種情況可以得出結論:根軌跡分支始於開環極點,終止於開環零點。
角度條件和幅值條件
根軌跡分支上的點滿足角度條件。因此,角度條件用於判斷點是否存在於根軌跡分支上。我們可以利用幅值條件找到根軌跡分支上點的 K 值。因此,我們可以對滿足角度條件的點使用幅值條件。
閉環控制系統的特徵方程為
$$1+G(s)H(s)=0$$
$$\Rightarrow G(s)H(s)=-1+j0$$
$G(s)H(s)$ 的相角為
$$\angle G(s)H(s)=\tan^{-1}\left ( \frac{0}{-1} \right )=(2n+1)\pi$$
角度條件是指開環傳遞函式的角度為 1800 的奇數倍的點。
$G(s)H(s)$ 的幅值為 −
$$|G(s)H(s)|=\sqrt {(-1)^2+0^2}=1$$
幅值條件是指(滿足角度條件的)開環傳遞函式幅值為 1 的點。
根軌跡的繪製
根軌跡是 s 域中的圖形表示,它關於實軸對稱。因為開環極點和零點存在於 s 域中,其值可以是實數或複共軛對。本章我們討論如何構造(繪製)根軌跡。
根軌跡繪製規則
遵循以下規則繪製根軌跡。
規則 1 − 在 ‘s’ 平面上定位開環極點和零點。
規則 2 − 找出根軌跡分支的數量。
我們知道根軌跡分支始於開環極點,終止於開環零點。因此,根軌跡分支數 N 等於有限開環極點數 P 或有限開環零點數 Z 中的較大者。
數學上,我們可以將根軌跡分支數 N 寫成
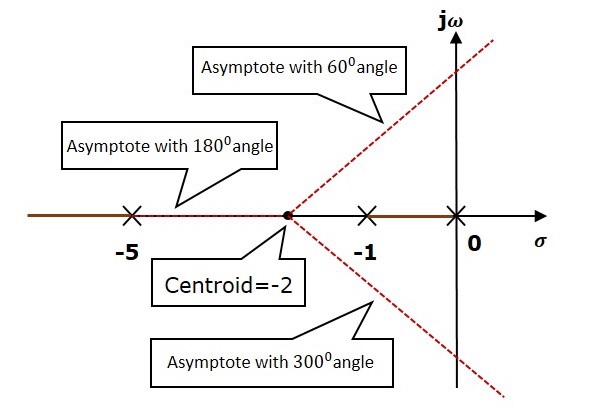
N=P,如果 $P\geq Z$
N=Z,如果 $P 規則 3 − 識別並繪製實軸根軌跡分支。 如果某點開環傳遞函式的角度為 1800 的奇數倍,則該點位於根軌跡上。如果實軸上某點左側存在奇數個開環極點和零點,則該點位於根軌跡分支上。因此,滿足此條件的點分支為根軌跡分支的實軸。 規則 4 − 找出漸近線的中心和角度。 如果 $P = Z$,則所有根軌跡分支都始於有限開環極點,終止於有限開環零點。 如果 $P > Z$,則 Z 個根軌跡分支始於有限開環極點,終止於有限開環零點,而 $P − Z$ 個根軌跡分支始於有限開環極點,終止於無限開環零點。 如果 $P < Z$,則 P 個根軌跡分支始於有限開環極點,終止於有限開環零點,而 $Z − P$ 個根軌跡分支始於無限開環極點,終止於有限開環零點。 因此,當 $P \neq Z$ 時,一些根軌跡分支趨於無窮大。漸近線給出這些根軌跡分支的方向。漸近線在實軸上的交點稱為中心。 我們可以用這個公式計算中心 α, $\alpha = \frac{\sum 有限開環極點的實部\:-\sum 有限開環零點的實部}{P-Z}$ 漸近線角度 θ 的公式為 $$\theta=\frac{(2q+1)180^0}{P-Z}$$ 其中: $$q=0,1,2,....,(P-Z)-1$$ 規則 5 − 找出根軌跡分支與虛軸的交點。 我們可以利用勞斯陣列法和特殊情況 (ii) 計算根軌跡分支與虛軸的交點以及該點的K 值。 如果勞斯陣列的任何一行的所有元素都為零,則根軌跡分支與虛軸相交,反之亦然。 以這樣的方式識別行:如果我們將第一個元素設為零,則整行的元素都為零。找到此組合的K 值。 將此K 值代入輔助方程。您將得到根軌跡分支與虛軸的交點。 規則 6 − 找出分離點和匯合點。 如果在兩個開環極點之間存在實軸根軌跡分支,則這兩個開環極點之間將存在一個分離點。 如果在兩個開環零點之間存在實軸根軌跡分支,則這兩個開環零點之間將存在一個匯合點。 注意 − 分離點和匯合點僅存在於實軸根軌跡分支上。 按照以下步驟查詢分離點和匯合點。 從特徵方程 $1 + G(s)H(s) = 0$ 中寫出 K 關於 s 的表示式。 對 K 關於 s 求導,並使其等於零。將這些 s 值代入上述方程。 K 值為正的 s 值是斷點。 規則 7 − 找出離去角和到達角。 分別可以在複共軛開環極點和複共軛開環零點處計算離去角和到達角。 離去角 $\phi_d$ 的公式為 $$\phi_d=180^0-\phi$$ 到達角 $\phi_a$ 的公式為 $$\phi_a=180^0+\phi$$ 其中: $$\phi=\sum \phi_P-\sum \phi_Z$$ 現在讓我們繪製具有開環傳遞函式 $G(s)H(s)=\frac{K}{s(s+1)(s+5)}$ 的控制系統的根軌跡。 步驟 1 − 給定的開環傳遞函式在 $s = 0, s = −1$ 和 $s = −5$ 處有三個極點。它沒有任何零點。因此,根軌跡分支的數量等於開環傳遞函式的極點數。 $$N=P=3$$ 三個極點的位置如上圖所示。$s = −1$ 和 $s = 0$ 之間的線段是實軸上根軌跡的一個分支。實軸上根軌跡的另一個分支是 $s = −5$ 左側的線段。 步驟 2 − 我們將使用給定的公式得到中心和漸近線角度的值。 中心 $\alpha = −2$ 漸近線角度為 $\theta = 60^0,180^0$ 和 $300^0$。 中心和三條漸近線如下圖所示。 步驟 3 − 由於兩條漸近線的角度為 $60^0$ 和 $300^0$,因此兩個根軌跡分支與虛軸相交。使用勞斯陣列法和特殊情況 (ii),根軌跡分支與虛軸在 $j\sqrt{5}$ 和 $−j\sqrt{5}$ 處相交。 在極點 $s = −1$ 和 $s = 0$ 之間的實軸根軌跡分支上將存在一個分離點。按照給出的計算分離點的步驟,我們將得到 $s = −0.473$。 給定控制系統的根軌跡圖如下圖所示。 透過這種方式,您可以繪製任何控制系統的根軌跡圖,並觀察閉環傳遞函式極點的移動。 從根軌跡圖中,我們可以知道不同型別阻尼的 K 值範圍。 可以透過新增開環極點和開環零點來移動‘s’ 平面中的根軌跡。 如果我們在開環傳遞函式中包含一個極點,則一些根軌跡分支將移向 ‘s’ 平面的右半部分。因此,阻尼比 $\delta$ 減小。這意味著阻尼頻率 $\omega_d$ 增加,時域指標如延遲時間 $t_d$、上升時間 $t_r$ 和峰值時間 $t_p$ 減小。但這會影響系統穩定性。 如果我們在開環傳遞函式中包含一個零點,則一些根軌跡分支將移向 ‘s’ 平面的左半部分。因此,它將提高控制系統的穩定性。在這種情況下,阻尼比 $\delta$ 增加。這意味著阻尼頻率 $\omega_d$ 減小,時域指標如延遲時間 $t_d$、上升時間 $t_r$ 和峰值時間 $t_p$ 增加。 因此,基於需求,我們可以將開環極點或零點包含(新增)到傳遞函式中。 我們已經討論了控制系統的時域響應分析和二階控制系統的時域指標。本章,我們討論控制系統的頻域響應分析和二階控制系統的頻域指標。 系統的響應可以分為瞬態響應和穩態響應。我們可以使用傅立葉積分求出瞬態響應。系統對正弦輸入訊號的穩態響應稱為頻域響應。本章,我們將只關注穩態響應。 如果將正弦訊號作為輸入應用於線性時不變 (LTI) 系統,則它會產生穩態輸出,該輸出也是正弦訊號。輸入和輸出正弦訊號具有相同的頻率,但幅度和相角不同。 設輸入訊號為 − $$r(t)=A\sin(\omega_0t)$$ 開環傳遞函式將為 − $$G(s)=G(j\omega)$$ 我們可以用如下所示的幅值和相位來表示 $G(j\omega)$。 $$G(j\omega)=|G(j\omega)| \angle G(j\omega)$$ 將$\omega = \omega_0$代入上式。 $$G(j\omega_0)=|G(j\omega_0)| \angle G(j\omega_0)$$ 輸出訊號為 $$c(t)=A|G(j\omega_0)|\sin(\omega_0t + \angle G(j\omega_0))$$ 輸出正弦訊號的幅度是透過將輸入正弦訊號的幅度與$G(j\omega)$在$\omega = \omega_0$處的幅值相乘得到的。 輸出正弦訊號的相位是透過將輸入正弦訊號的相位與$G(j\omega)$在$\omega = \omega_0$處的相位相加得到的。 其中: A是輸入正弦訊號的幅度。 ω0是輸入正弦訊號的角頻率。 我們可以將角頻率$\omega_0$寫成如下形式: $$\omega_0=2\pi f_0$$ 這裡,$f_0$是輸入正弦訊號的頻率。同樣,對於閉環控制系統,您可以遵循相同的步驟。 頻域指標為諧振峰值、諧振頻率和頻寬。 考慮二階閉環控制系統的傳遞函式為: $$T(s)=\frac{C(s)}{R(s)}=\frac{\omega_n^2}{s^2+2\delta\omega_ns+\omega_n^2}$$ 將$s = j\omega$代入上式。 $$T(j\omega)=\frac{\omega_n^2}{(j\omega)^2+2\delta\omega_n(j\omega)+\omega_n^2}$$ $$\Rightarrow T(j\omega)=\frac{\omega_n^2}{-\omega^2+2j\delta\omega\omega_n+\omega_n^2}=\frac{\omega_n^2}{\omega_n^2\left ( 1-\frac{\omega^2}{\omega_n^2}+\frac{2j\delta\omega}{\omega_n} \right )}$$ $$\Rightarrow T(j\omega)=\frac{1}{\left ( 1-\frac{\omega^2}{\omega_n^2} \right )+j\left ( \frac{2\delta\omega}{\omega_n} \right )}$$ 令$\frac{\omega}{\omega_n}=u$,並將此值代入上式。 $$T(j\omega)=\frac{1}{(1-u^2)+j(2\delta u)}$$ $T(j\omega)$的幅值為: $$M=|T(j\omega)|=\frac{1}{\sqrt {(1-u^2)^2+(2\delta u)^2}}$$ $T(j\omega)$的相位為: $$\angle T(j\omega)=-tan^{-1}\left( \frac{2\delta u}{1-u^2} \right )$$ 它是頻率響應的幅值第一次達到峰值的頻率。用$\omega_r$表示。在$\omega = \omega_r$時,$T(j\omega)$幅值的導數為零。 對M關於u求導。 $$\frac{\text{d}M}{\text{d}u}=-\frac{1}{2}\left [ (1-u^2)^2+(2\delta u)^2 \right ]^{\frac{-3}{2}} \left [2(1-u^2)(-2u)+2(2\delta u)(2\delta) \right ]$$ $$\Rightarrow \frac{\text{d}M}{\text{d}u}=-\frac{1}{2}\left [ (1-u^2)^2+(2\delta u)^2 \right ]^{\frac{-3}{2}} \left [4u(u^2-1 +2\delta^2) \right ]$$ 將$u=u_r$和$\frac{\text{d}M}{\text{d}u}==0$代入上式。 $$0=-\frac{1}{2}\left [ (1-u_r^2)^2+(2\delta u_r)^2 \right ]^{-\frac{3}{2}}\left [ 4u_r(u_r^2-1 +2\delta^2) \right ]$$ $$\Rightarrow 4u_r(u_r^2-1 +2\delta^2)=0$$ $$\Rightarrow u_r^2-1+2\delta^2=0$$ $$\Rightarrow u_r^2=1-2\delta^2$$ $$\Rightarrow u_r=\sqrt{1-2\delta^2}$$ 將$u_r=\frac{\omega_r}{\omega_n}$代入上式。 $$\frac{\omega_r}{\omega_n}=\sqrt{1-2\delta^2}$$ $$\Rightarrow \omega_r=\omega_n \sqrt{1-2\delta^2}$$ 它是$T(j\omega)$幅值的峰值(最大值)。用$M_r$表示。 在$u = u_r$時,$T(j\omega)$的幅值為: $$M_r=\frac{1}{\sqrt{(1-u_r^2)^2+(2\delta u_r)^2}}$$ 將$u_r = \sqrt{1 − 2\delta^2}$和$1 − u_r^2 = 2\delta^2$代入上式。 $$M_r=\frac{1}{\sqrt{(2\delta^2)^2+(2\delta \sqrt{1-2\delta^2})^2}}$$ $$\Rightarrow M_r=\frac{1}{2\delta \sqrt {1-\delta^2}}$$ 頻率響應中的諧振峰值與某些阻尼比$\delta$值下的時域瞬態響應中的峰值超調量相關。因此,諧振峰值和峰值超調量是相互關聯的。 它是$T(j\omega)$的幅值從其零頻率值下降到70.7%的頻率範圍。 在$\omega = 0$時,u的值為零。 將$u = 0$代入M。 $$M=\frac{1}{\sqrt {(1-0^2)^2+(2\delta(0))^2}}=1$$ 因此,$T(j\omega)$的幅值在$\omega = 0$時為1。 在3-dB頻率處,$T(j\omega)$的幅值將是$T(j\omega)$在$\omega = 0$處幅值的70.7%。 即,在$\omega = \omega_B$處,$M = 0.707(1) = \frac{1}{\sqrt{2}}$ $$\Rightarrow M=\frac{1}{\sqrt{2}}=\frac{1}{\sqrt{(1-u_b^2)^2+(2\delta u_b)^2}}$$ $$\Rightarrow 2=(1-u_b^2)^2+(2\delta)^2 u_b^2$$ 令$u_b^2=x$ $$\Rightarrow 2=(1-x)^2+(2\delta)^2 x$$ $$\Rightarrow x^2+(4\delta^2-2)x-1=0$$ $$\Rightarrow x=\frac{-(4\delta^2 -2)\pm \sqrt{(4\delta^2-2)^2+4}}{2}$$ 只考慮x的正值。 $$x=1-2\delta^2+\sqrt {(2\delta^2-1)^2+1}$$ $$\Rightarrow x=1-2\delta^2+\sqrt {(2-4\delta^2+4\delta^4)}$$ 將$x=u_b^2=\frac{\omega_b^2}{\omega_n^2}$代入。 $$\frac{\omega_b^2}{\omega_n^2}=1-2\delta^2+\sqrt {(2-4\delta^2+4\delta^4)}$$ $$\Rightarrow \omega_b=\omega_n \sqrt {1-2\delta^2+\sqrt {(2-4\delta^2+4\delta^4)}}$$ 頻率響應中的頻寬$\omega_b$與時域瞬態響應中的上升時間$t_r$成反比。 伯德圖或伯德圖由兩幅圖組成: 在這兩幅圖中,x軸表示角頻率(對數刻度)。而y軸在幅頻特性圖中表示開環傳遞函式的幅值(線性刻度),在相頻特性圖中表示開環傳遞函式的相角(線性刻度)。 開環傳遞函式的幅值(以dB表示)為: $$M=20\: \log|G(j\omega)H(j\omega)|$$ 開環傳遞函式的相角(以度表示)為: $$\phi=\angle G(j\omega)H(j\omega)$$ 注意 - 對數的底數為10。 下表顯示了開環傳遞函式中各分母項的斜率、幅值和相角值。繪製伯德圖時,這些資料非常有用。 常數 $K$ $0$ $20 \log K$ $0$ 原點零點 $j\omega$ $20$ $20 \log \omega$ $90$ ‘n’個原點零點 $(j\omega)^n$ $20\: n$ $20\: n \log \omega$ $90\: n$ 原點極點 $\frac{1}{j\omega}$ $-20$ $-20 \log \omega$ $-90 \: or \: 270$ ‘n’個原點極點 $\frac{1}{(j\omega)^n}$ $-20\: n$ $-20 \: n \log \omega$ $-90 \: n \: or \: 270 \: n$ 簡單零點 $1+j\omega r$ $20$ $0\: for\: \omega < \frac{1}{r}$ $20\: \log \omega r\: for \: \omega > \frac{1}{r}$ $0 \: for \: \omega < \frac{1}{r}$ $90 \: for \: \omega > \frac{1}{r}$ 簡單極點 $\frac{1}{1+j\omega r}$ $-20$ $0\: for\: \omega < \frac{1}{r}$ $-20\: \log \omega r\: for\: \omega > \frac{1}{r}$ $0 \: for \: \omega < \frac{1}{r}$ $-90\: or \: 270 \: for\: \omega > \frac{1}{r}$ 二階導數項 $\omega_n^2\left ( 1-\frac{\omega^2}{\omega_n^2}+\frac{2j\delta\omega}{\omega_n} \right )$ $40$ $40\: \log\: \omega_n\: for \: \omega < \omega_n$ $20\: \log\:(2\delta\omega_n^2)\: for \: \omega=\omega_n$ $40 \: \log \: \omega\:for \:\omega > \omega_n$ $0 \: for \: \omega < \omega_n$ $90 \: for \: \omega = \omega_n$ $180 \: for \: \omega > \omega_n$ 二階積分項 $\frac{1}{\omega_n^2\left ( 1-\frac{\omega^2}{\omega_n^2}+\frac{2j\delta\omega}{\omega_n} \right )}$ $-40$ $-40\: \log\: \omega_n\: for \: \omega < \omega_n$ $-20\: \log\:(2\delta\omega_n^2)\: for \: \omega=\omega_n$ $-40 \: \log \: \omega\:for \:\omega > \omega_n$ $-0 \: for \: \omega < \omega_n$ $-90 \: for \: \omega = \omega_n$ $-180 \: for \: \omega > \omega_n$ 考慮開環傳遞函式$G(s)H(s) = K$。 幅值 $M = 20\: \log K$ dB 相角 $\phi = 0$ 度 如果$K = 1$,則幅值為0 dB。 如果$K > 1$,則幅值將為正。 如果$K < 1$,則幅值將為負。 下圖顯示了相應的伯德圖。 幅頻特性圖是一條水平線,與頻率無關。當K值為1時,0 dB線本身就是幅頻特性圖。對於K的正值,水平線將向上移動$20 \:\log K$ dB。對於K的負值,水平線將向下移動$20\: \log K$ dB。對於K的所有正值,零度線本身就是相頻特性圖。 考慮開環傳遞函式$G(s)H(s) = s$。 幅值 $M = 20 \log \omega$ dB 相角 $\phi = 90^0$ 在$\omega = 0.1$ rad/sec時,幅值為-20 dB。 在$\omega = 1$ rad/sec時,幅值為0 dB。 在$\omega = 10$ rad/sec時,幅值為20 dB。 下圖顯示了相應的伯德圖。 幅頻特性圖是一條斜率為20 dB/dec的直線。這條線從$\omega = 0.1$ rad/sec開始,幅值為-20 dB,並沿相同的斜率繼續延伸。它在$\omega = 1$ rad/sec處與0 dB線相交。在這種情況下,相頻特性圖是900線。 考慮開環傳遞函式$G(s)H(s) = 1 + s\tau$。 幅值 $M = 20\: log \sqrt{1 + \omega^2\tau^2}$ dB 相角 $\phi = \tan^{-1}\omega\tau$ 度 對於$ω < \frac{1}{\tau}$,幅值為0 dB,相角為0度。 對於$\omega > \frac{1}{\tau}$,幅值為$20\: \log \omega\tau$ dB,相角為900。 下圖顯示了相應的伯德圖。 幅頻特性圖在$\omega=\frac{1}{\tau}$ rad/sec之前幅值為0 dB。從$\omega = \frac{1}{\tau}$ rad/sec開始,其斜率為20 dB/dec。在這種情況下,相頻特性圖在$\omega = \frac{1}{\tau}$ rad/sec之前相角為0度,從這裡開始,其相角為900。這個伯德圖被稱為漸近伯德圖。 由於幅頻特性圖和相頻特性圖都用直線表示,因此精確的伯德圖與漸近伯德圖相似。唯一的區別在於精確的伯德圖將具有簡單的曲線而不是直線。 同樣,您可以為表中給出的開環傳遞函式的其他項繪製伯德圖。 在本章中,讓我們詳細瞭解如何繪製伯德圖。 繪製伯德圖時,請遵循以下規則。 將開環傳遞函式表示為標準時間常數形式。 將$s=j\omega$代入上式。 找到轉折頻率,並按升序排列。 將伯德圖的起始頻率視為最小轉折頻率的1/10或0.1 rad/sec(取較小值),並繪製到最大轉折頻率的10倍。 為每一項繪製幅頻特性圖,並將這些圖正確地組合起來。 為每一項繪製相頻特性圖,並將這些圖正確地組合起來。 注意 - 轉折頻率是幅頻特性圖斜率發生變化的頻率。 考慮閉環控制系統的開環傳遞函式 $$G(s)H(s)=\frac{10s}{(s+2)(s+5)}$$ 讓我們將這個開環傳遞函式轉換為標準時間常數形式。 $$G(s)H(s)=\frac{10s}{2\left( \frac{s}{2}+1 \right )5 \left( \frac{s}{5}+1 \right )}$$ $$\Rightarrow G(s)H(s)=\frac{s}{\left( 1+\frac{s}{2} \right )\left( 1+\frac{s}{5} \right )}$$ 因此,我們可以使用前面提到的規則在半對數座標紙上繪製伯德圖。 從伯德圖中,我們可以根據這些引數的值判斷控制系統是穩定的、臨界穩定的還是不穩定的。 相頻特性圖的相位為-1800的頻率稱為相位交越頻率。用$\omega_{pc}$表示。相位交越頻率的單位為rad/sec。 幅值曲線幅值為0dB時的頻率稱為增益穿越頻率,用$\omega_{gc}$表示。增益穿越頻率的單位為rad/sec。 控制系統的穩定性取決於相位穿越頻率和增益穿越頻率之間的關係,如下所示。 如果相位穿越頻率$\omega_{pc}$大於增益穿越頻率$\omega_{gc}$,則控制系統為穩定的。 如果相位穿越頻率$\omega_{pc}$等於增益穿越頻率$\omega_{gc}$,則控制系統為臨界穩定的。 如果相位穿越頻率$\omega_{pc}$小於增益穿越頻率$\omega_{gc}$,則控制系統為不穩定的。 增益裕度$GM$等於相位穿越頻率下幅值(dB)的負值。 $$GM=20\log\left( \frac{1}{M_{pc}}\right )= -20\log{M_{pc}}$$ 其中,$M_{pc}$是相位穿越頻率下的幅值。增益裕度(GM)的單位為dB。 相位裕度$PM$的公式為 $$PM=180^0+\phi_{gc}$$ 其中,$\phi_{gc}$是增益穿越頻率下的相位角。相位裕度的單位為度。 控制系統的穩定性取決於增益裕度和相位裕度之間的關係,如下所示。 如果增益裕度$GM$和相位裕度$PM$均為正,則控制系統為穩定的。 如果增益裕度$GM$和相位裕度$PM$均為零,則控制系統為臨界穩定的。 如果增益裕度$GM$和/或相位裕度$PM$為負,則控制系統為不穩定的。 在前面的章節中,我們討論了Bode圖。在那裡,我們分別繪製了幅值和相位與頻率的關係圖。現在讓我們討論極座標圖。極座標圖是在幅值和相位之間繪製的曲線圖。這裡,幅值僅用普通值表示。 $G(j\omega)H(j\omega)$的極座標形式為 $$G(j\omega)H(j\omega)=|G(j\omega)H(j\omega)| \angle G(j\omega)H(j\omega)$$ 極座標圖是透過改變$\omega$從零到∞,在$G(j\omega)H(j\omega)$的幅值和相位角之間繪製的曲線圖。極座標圖紙如下所示。 該圖紙由同心圓和徑向線組成。同心圓和徑向線分別表示幅值和相位角。這些角度以逆時針方向的正值表示。類似地,我們可以用順時針方向的負值表示角度。例如,逆時針方向的2700角等於順時針方向的−900角。 遵循以下規則繪製極座標圖。 在開環傳遞函式中代入$s = j\omega$。 寫出$G(j\omega)H(j\omega)$的幅值和相位的表示式。 透過代入$\omega = 0$,找到$G(j\omega)H(j\omega)$的起始幅值和相位。因此,極座標圖從此幅值和相位角開始。 透過代入$\omega = \infty$,找到$G(j\omega)H(j\omega)$的結束幅值和相位。因此,極座標圖以此幅值和相位角結束。 透過使$G(j\omega)H(j\omega)$的虛部等於零並找到$\omega$的值,檢查極座標圖是否與實軸相交。 透過使$G(j\omega)H(j\omega)$的實部等於零並找到$\omega$的值,檢查極座標圖是否與虛軸相交。 為了更清晰地繪製極座標圖,請考慮$\omega$的其他值,找到$G(j\omega)H(j\omega)$的幅值和相位。 考慮閉環控制系統的開環傳遞函式。 $$G(s)H(s)=\frac{5}{s(s+1)(s+2)}$$ 讓我們使用上述規則繪製該控制系統的極座標圖。 步驟1 - 在開環傳遞函式中代入$s = j\omega$。 $$G(j\omega)H(j\omega)=\frac{5}{j\omega(j\omega+1)(j\omega+2)}$$ 開環傳遞函式的幅值為 $$M=\frac{5}{\omega(\sqrt{\omega^2+1})(\sqrt{\omega^2+4})}$$ 開環傳遞函式的相位角為 $$\phi=-90^0-\tan^{-1}\omega-\tan^{-1}\frac{\omega}{2}$$ 步驟2 - 下表顯示了開環傳遞函式在$\omega = 0$ rad/sec和$\omega = \infty$ rad/sec時的幅值和相位角。 -270 或 90 因此,極座標圖從(∞,−900)開始,在(0,−2700)結束。括號中的第一項和第二項分別表示幅值和相位角。 步驟3 - 基於起始和結束極座標,該極座標圖將與負實軸相交。對應於負實軸的相位角為−1800或1800。因此,透過將開環傳遞函式的相位角等於−1800或1800,我們將得到$\omega$值為$\sqrt{2}$。 透過在開環傳遞函式的幅值中代入$\omega = \sqrt{2}$,我們將得到$M = 0.83$。因此,當$\omega = \sqrt{2}$時,極座標圖與負實軸相交,極座標為(0.83,−1800)。 因此,我們可以使用上述資訊在極座標圖紙上繪製極座標圖。 奈奎斯特穩定性判據 奈奎斯特穩定性判據基於幅角原理。它指出,如果's'平面閉合路徑包含P個極點和Z個零點,則對應的$G(s)H(s)$平面必須繞原點旋轉$P − Z$圈。因此,我們可以將環繞數N寫成: $$N=P-Z$$ 如果封閉的's'平面閉合路徑僅包含極點,則$G(s)H(s)$平面中環繞的方向將與's'平面中封閉閉合路徑的方向相反。 如果封閉的's'平面閉合路徑僅包含零點,則$G(s)H(s)$平面中環繞的方向將與's'平面中封閉閉合路徑的方向相同。 現在讓我們透過將其選為閉合路徑,將幅角原理應用於's'平面的整個右半部分。此選擇的路徑稱為奈奎斯特輪廓。 我們知道,如果閉環傳遞函式的所有極點都在's'平面的左半部分,則閉環控制系統是穩定的。因此,閉環傳遞函式的極點就是特徵方程的根。隨著特徵方程階數的增加,很難找到根。因此,讓我們關聯這些特徵方程的根,如下所示。 特徵方程的極點與開環傳遞函式的極點相同。 特徵方程的零點與閉環傳遞函式的極點相同。 我們知道,如果's'平面的右半部分沒有開環極點,則開環控制系統是穩定的。 即,$P=0 \Rightarrow N=-Z$ 我們知道,如果's'平面的右半部分沒有閉環極點,則閉環控制系統是穩定的。 即,$Z=0 \Rightarrow N=P$ 繪製奈奎斯特圖的規則 遵循以下規則繪製奈奎斯特圖。 在's'平面上找到開環傳遞函式$G(s)H(s)$的極點和零點。 透過將$\omega$從零變到無窮大來繪製極座標圖。如果極點或零點出現在s = 0處,則在繪製極座標圖時將ω從0+變到無窮大。 繪製上述極座標圖在ω範圍從−∞到零(如果s=0處存在任何極點或零點,則為0−)時的映象。 無窮大半圓的個數將等於原點處極點或零點的個數。無窮大半圓將從極座標圖映象結束的點開始。這個無窮大半圓將結束在極座標圖開始的點。 使用奈奎斯特圖進行穩定性分析 從奈奎斯特圖中,我們可以根據這些引數的值確定控制系統是穩定、臨界穩定還是不穩定。 奈奎斯特圖與負實軸相交(相位角為1800)時的頻率稱為相位穿越頻率,用$\omega_{pc}$表示。 奈奎斯特圖幅值為1時的頻率稱為增益穿越頻率,用$\omega_{gc}$表示。 如果相位穿越頻率$\omega_{pc}$大於增益穿越頻率$\omega_{gc}$,則控制系統為穩定的。 如果相位穿越頻率$\omega_{pc}$等於增益穿越頻率$\omega_{gc}$,則控制系統為臨界穩定的。 控制系統的穩定性取決於相位穿越頻率和增益穿越頻率之間的關係,如下所示。 如果相位穿越頻率$\omega_{pc}$小於增益穿越頻率$\omega_{gc}$,則控制系統為不穩定的。 增益裕度$GM$等於奈奎斯特圖在相位穿越頻率下幅值的倒數。 $$GM=\frac{1}{M_{pc}}$$ 其中,$M_{pc}$是相位穿越頻率下普通比例尺的幅值。 $$PM=180^0+\phi_{gc}$$ 相位裕度$PM$等於1800與增益穿越頻率下相位角的和。 $$PM = 180^\circ + \phi_{gc}$$ 其中,$\phi_{gc}$是增益穿越頻率下的相位角。 控制系統的穩定性取決於增益裕度和相位裕度之間的關係,如下所示。 如果增益裕度$GM$大於1且相位裕度$PM$為正,則控制系統為穩定的。 如果增益裕度$GM$等於1且相位裕度$PM$為零度,則控制系統為臨界穩定的。 補償器有三種類型:滯後、超前和滯後-超前補償器。這些是最常用的。 滯後補償器 該滯後補償器的傳遞函式為: $$ \frac{V_o(s)}{V_i(s)} = \frac{1}{\alpha} \left( \frac{s + \frac{1}{\tau}}{s + \frac{1}{\alpha\tau}} \right) $$ 其中: $$ \tau = R_2C $$ $$ \alpha = \frac{R_1 + R_2}{R_2} $$ 從上式可以看出,α 總是大於 1。 從傳遞函式可以看出,滯後補償器在 s = −1/(ατ) 處有一個極點,在 s = −1/τ 處有一個零點。這意味著在滯後補償器的零極點配置中,極點更靠近原點。 將 s = jω 代入傳遞函式。 $$ \frac{V_o(j\omega)}{V_i(j\omega)} = \frac{1}{\alpha} \left( \frac{j\omega + \frac{1}{\tau}}{j\omega + \frac{1}{\alpha\tau}} \right) $$ 相位角 φ = arctan(ωτ) − arctan(αωτ) 我們知道,輸出正弦訊號的相位等於輸入正弦訊號和傳遞函式的相位角之和。 因此,為了在該補償器的輸出端產生相位滯後,傳遞函式的相位角應為負值。當 α > 1 時,這種情況就會發生。 超前補償器是一種電網路,當施加正弦輸入時,它會產生具有相位超前的正弦輸出。's' 域中的超前補償器電路如下圖所示。 這裡,電容與電阻 R₁ 並聯,輸出在電阻 R₂ 上測量。 該超前補償器的傳遞函式為: $$ \frac{V_o(s)}{V_i(s)} = \beta \left( \frac{s\tau + 1}{\beta s\tau + 1} \right) $$ 其中: $$ \tau = R_1C $$ $$ \beta = \frac{R_2}{R_1 + R_2} $$ 從傳遞函式可以看出,超前補償器在 s = −1/β 處有一個極點,在 s = −1/(βτ) 處有一個零點。 將 s = jω 代入傳遞函式。 $$ \frac{V_o(j\omega)}{V_i(j\omega)} = \beta \left( \frac{j\omega\tau + 1}{\beta j\omega\tau + 1} \right) $$ 相位角 φ = arctan(ωτ) − arctan(βωτ) 我們知道,輸出正弦訊號的相位等於輸入正弦訊號和傳遞函式的相位角之和。 因此,為了在該補償器的輸出端產生相位超前,傳遞函式的相位角應為正值。當 0 < β < 1 時,這種情況就會發生。因此,在超前補償器的零極點配置中,零點更靠近原點。 滯後-超前補償器是一種電網路,它在一個頻率區域產生相位滯後,而在另一個頻率區域產生相位超前。它是滯後補償器和超前補償器的組合。's' 域中的滯後-超前補償器電路如下圖所示。 該電路看起來像是兩個補償器級聯連線。因此,該電路的傳遞函式將是超前補償器和滯後補償器傳遞函式的乘積。 $$ \frac{V_o(s)}{V_i(s)} = \beta \left( \frac{s\tau_1 + 1}{\beta s\tau_1 + 1} \right) \frac{1}{\alpha} \left( \frac{s + \frac{1}{\tau_2}}{s + \frac{1}{\alpha\tau_2}} \right) $$ 我們知道 αβ = 1。 $$ \Rightarrow \frac{V_o(s)}{V_i(s)} = \left( \frac{s + \frac{1}{\tau_1}}{s + \frac{1}{\beta\tau_1}} \right) \left( \frac{s + \frac{1}{\tau_2}}{s + \frac{1}{\alpha\tau_2}} \right) $$ 其中: $$ \tau_1 = R_1C_1 $$ $$ \tau_2 = R_2C_2 $$ 各種型別的控制器用於提高控制系統的效能。本章將討論基本的控制器,例如比例、微分和積分控制器。 比例控制器產生一個與誤差訊號成比例的輸出。 $$ u(t) \propto e(t) $$ $$ \Rightarrow u(t) = K_P e(t) $$ 對兩邊進行拉普拉斯變換: $$ U(s) = K_P E(s) $$ $$ \frac{U(s)}{E(s)} = K_P $$ 因此,比例控制器的傳遞函式為 KP。 其中: U(s) 是執行訊號 u(t) 的拉普拉斯變換 E(s) 是誤差訊號 e(t) 的拉普拉斯變換 KP 是比例常數 帶有比例控制器的單位負反饋閉環控制系統的框圖如下圖所示。 比例控制器用於根據要求更改暫態響應。 微分控制器產生一個為誤差訊號導數的輸出。 $$ u(t) = K_D \frac{de(t)}{dt} $$ 對等式兩邊進行拉普拉斯變換。 $$ U(s) = K_D sE(s) $$ $$ \frac{U(s)}{E(s)} = K_D s $$ 因此,微分控制器的傳遞函式為 KDs。 其中,KD 是微分常數。 帶有微分控制器的單位負反饋閉環控制系統的框圖如下圖所示。 微分控制器用於將不穩定的控制系統變為穩定的控制系統。 積分控制器產生一個為誤差訊號積分的輸出。 $$ u(t) = K_I \int e(t) dt $$ 對兩邊進行拉普拉斯變換: $$ U(s) = \frac{K_I E(s)}{s} $$ $$ \frac{U(s)}{E(s)} = \frac{K_I}{s} $$ 因此,積分控制器的傳遞函式為 KI/s。 其中,KI 是積分常數。 帶有積分控制器的單位負反饋閉環控制系統的框圖如下圖所示。 積分控制器用於減小穩態誤差。 現在讓我們討論一下基本控制器的組合。 比例微分控制器產生一個比例控制器和微分控制器的輸出組合的輸出。 $$ u(t) = K_P e(t) + K_D \frac{de(t)}{dt} $$ 對兩邊進行拉普拉斯變換: $$ U(s) = (K_P + K_D s)E(s) $$ $$ \frac{U(s)}{E(s)} = K_P + K_D s $$ 因此,比例微分控制器的傳遞函式為 KP + KDs。 帶有比例微分控制器的單位負反饋閉環控制系統的框圖如下圖所示。 比例微分控制器用於提高控制系統的穩定性,而不影響穩態誤差。 比例積分控制器產生一個比例控制器和積分控制器的輸出組合的輸出。 $$ u(t) = K_P e(t) + K_I \int e(t) dt $$ 對兩邊進行拉普拉斯變換: $$ U(s) = \left( K_P + \frac{K_I}{s} \right) E(s) $$ $$ \frac{U(s)}{E(s)} = K_P + \frac{K_I}{s} $$ 因此,比例積分控制器的傳遞函式為 KP + KI/s。 帶有比例積分控制器的單位負反饋閉環控制系統的框圖如下圖所示。 比例積分控制器用於減小穩態誤差,而不影響控制系統的穩定性。 比例積分微分控制器產生一個比例、積分和微分控制器的輸出組合的輸出。 $$ u(t) = K_P e(t) + K_I \int e(t) dt + K_D \frac{de(t)}{dt} $$ 對兩邊進行拉普拉斯變換: $$ U(s) = \left( K_P + \frac{K_I}{s} + K_D s \right) E(s) $$ $$ \frac{U(s)}{E(s)} = K_P + \frac{K_I}{s} + K_D s $$ 因此,比例積分微分控制器的傳遞函式為 KP + KI/s + KDs。 帶有比例積分微分控制器的單位負反饋閉環控制系統的框圖如下圖所示。 比例積分微分控制器用於提高控制系統的穩定性並減小穩態誤差。 線性時不變 (LTI) 系統的狀態空間模型可以表示為: $$ \dot{X} = AX + BU $$ $$ Y = CX + DU $$ 第一和第二個方程分別稱為狀態方程和輸出方程。 其中: X 和 $\dot{X}$ 分別是狀態向量和微分狀態向量。 U 和 Y 分別是輸入向量和輸出向量。 A 是系統矩陣。 B 和 C 是輸入和輸出矩陣。 D 是前饋矩陣。 本章涉及以下基本術語。 它是一組變數,用於總結系統的歷史,以便預測未來的值(輸出)。 所需狀態變數的數量等於系統中存在的儲存元件的數量。 示例 - 流過電感的電流,跨電容的電壓 它是一個向量,包含狀態變數作為元素。 在前面的章節中,我們討論了控制系統的兩種數學模型。它們是微分方程模型和傳遞函式模型。狀態空間模型可以從這兩個數學模型中的任何一個獲得。現在讓我們逐一討論這兩種方法。 考慮以下 RLC 串聯電路。它有一個輸入電壓 vi(t),電路中流過的電流為 i(t)。 該電路中有兩個儲存元件(電感和電容)。因此,狀態變數的數量等於二,這些狀態變數是流過電感的電流 i(t) 和跨電容的電壓 vc(t)。 從電路圖中,輸出電壓 vo(t) 等於跨電容的電壓 vc(t)。 $$ v_o(t) = v_c(t) $$ 應用 KVL 環路定律。 $$ v_i(t) = Ri(t) + L\frac{di(t)}{dt} + v_c(t) $$ $$ \Rightarrow \frac{di(t)}{dt} = -\frac{Ri(t)}{L} - \frac{v_c(t)}{L} + \frac{v_i(t)}{L} $$ 跨電容的電壓為: $$ v_c(t) = \frac{1}{C} \int i(t) dt $$ 對上式關於時間求導。 $$ \frac{dv_c(t)}{dt} = \frac{i(t)}{C} $$ 狀態向量,X = $\begin{bmatrix} i(t) \\ v_c(t) \end{bmatrix}$ 微分狀態向量,$\dot{X} = \begin{bmatrix} \frac{di(t)}{dt} \\ \frac{dv_c(t)}{dt} \end{bmatrix}$ 我們可以將微分方程和輸出方程排列成狀態空間模型的標準形式,如下所示: $$ \dot{X} = \begin{bmatrix} \frac{di(t)}{dt} \\ \frac{dv_c(t)}{dt} \end{bmatrix} = \begin{bmatrix} -\frac{R}{L} & -\frac{1}{L} \\ \frac{1}{C} & 0 \end{bmatrix} \begin{bmatrix} i(t) \\ v_c(t) \end{bmatrix} + \begin{bmatrix} \frac{1}{L} \\ 0 \end{bmatrix} \begin{bmatrix} v_i(t) \end{bmatrix} $$ $$ Y = \begin{bmatrix} 0 & 1 \end{bmatrix} \begin{bmatrix} i(t) \\ v_c(t) \end{bmatrix} $$ 其中: $$ A = \begin{bmatrix} -\frac{R}{L} & -\frac{1}{L} \\ \frac{1}{C} & 0 \end{bmatrix}, \: B = \begin{bmatrix} \frac{1}{L} \\ 0 \end{bmatrix}, \: C = \begin{bmatrix} 0 & 1 \end{bmatrix} \: 和 \: D = \begin{bmatrix} 0 \end{bmatrix} $$ 考慮基於分子中存在的項型別的兩種傳遞函式。 考慮以下系統的傳遞函式 $$ \frac{Y(s)}{U(s)} = \frac{b_0}{s^n + a_{n-1}s^{n-1} + ... + a_1s + a_0} $$ 重新排列上述等式為 $$ (s^n + a_{n-1}s^{n-1} + ... + a_0)Y(s) = b_0 U(s) $$ 對兩邊應用拉普拉斯逆變換。 $$ \frac{d^ny(t)}{dt^n} + a_{n-1}\frac{d^{n-1}y(t)}{dt^{n-1}} + ... + a_1\frac{dy(t)}{dt} + a_0y(t) = b_0 u(t) $$ 令 $$ y(t) = x_1 $$ $$ \frac{dy(t)}{dt} = x_2 = \dot{x}_1 $$ $$ \frac{d^2y(t)}{dt^2} = x_3 = \dot{x}_2 $$ $$.$$ $$.$$ $$.$$ $$ \frac{d^{n-1}y(t)}{dt^{n-1}} = x_n = \dot{x}_{n-1} $$ $$ \frac{d^ny(t)}{dt^n} = \dot{x}_n $$ 和 u(t) = u 然後, $$ \dot{x}_n + a_{n-1}x_n + ... + a_1x_2 + a_0x_1 = b_0 u $$ 從上述等式,我們可以寫出以下狀態方程。 $$ \dot{x}_n = -a_0x_1 - a_1x_2 - ... - a_{n-1}x_n + b_0 u $$ 輸出方程為: $$ y(t) = y = x_1 $$ 狀態空間模型為: $\dot{X} = \begin{bmatrix} \dot{x}_1 \\ \dot{x}_2 \\ \vdots \\ \dot{x}_{n-1} \\ \dot{x}_n \end{bmatrix}$ $$=\begin{bmatrix}0 & 1 & 0 & \cdots & 0 & 0 \\0 & 0 & 1 & \cdots & 0 & 0 \\\vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & 0 & \cdots & 0 & 1 \\-a_0 & -a_1 & -a_2 & \cdots & -a_{n-2} & -a_{n-1} \end{bmatrix} \begin{bmatrix}x_1 \\x_2 \\\vdots \\x_{n-1} \\x_n \end{bmatrix}+\begin{bmatrix}0 \\0 \\\vdots \\0 \\b_0 \end{bmatrix}\begin{bmatrix}u \end{bmatrix}$$ $$Y=\begin{bmatrix}1 & 0 & \cdots & 0 & 0 \end{bmatrix}\begin{bmatrix}x_1 \\x_2 \\\vdots \\x_{n-1} \\x_n \end{bmatrix}$$ 此處,$D=\left [ 0 \right ]$。 求具有下列傳遞函式的系統的狀態空間模型。 $$ \frac{Y(s)}{U(s)}=\frac{1}{s^2+s+1} $$ 將上述方程改寫為: $$ (s^2+s+1)Y(s)=U(s) $$ 對兩邊應用拉普拉斯逆變換。 $$ \frac{\text{d}^2y(t)}{\text{d}t^2}+\frac{\text{d}y(t)}{\text{d}t}+y(t)=u(t) $$ 令 $$ y(t) = x_1 $$ $$ \frac{dy(t)}{dt} = x_2 = \dot{x}_1 $$ 和 u(t) = u 則狀態方程為 $$ \dot{x}_2=-x_1-x_2+u $$ 輸出方程為 $$ y(t) = y = x_1 $$ 狀態空間模型為 $$ \dot{X}=\begin{bmatrix}\dot{x}_1 \\\dot{x}_2 \end{bmatrix}=\begin{bmatrix}0 & 1 \\-1 & -1 \end{bmatrix}\begin{bmatrix}x_1 \\x_2 \end{bmatrix}+\begin{bmatrix}0 \\1 \end{bmatrix}\left [u \right ] $$ $$ Y=\begin{bmatrix}1 & 0 \end{bmatrix}\begin{bmatrix}x_1 \\x_2 \end{bmatrix} $$ 考慮以下系統的傳遞函式 $$ \frac{Y(s)}{U(s)}=\frac{b_n s^n+b_{n-1}s^{n-1}+...+b_1s+b_0}{s^n+a_{n-1}s^{n-1}+...+a_1 s+a_0} $$ $$ \Rightarrow \frac{Y(s)}{U(s)}=\left( \frac{1}{s^n+a_{n-1}s^{n-1}+...+a_1 s+a_0} \right )(b_n s^n+b_{n-1}s^{n-1}+...+b_1s+b_0) $$ 上述方程是兩個級聯模組的傳遞函式乘積的形式。 $$ \frac{Y(s)}{U(s)}=\left(\frac{V(s)}{U(s)} \right ) \left(\frac{Y(s)}{V(s)} \right ) $$ 此處, $$ \frac{V(s)}{U(s)}=\frac{1}{s^n+a_{n-1}s^{n-1}+...+a_1 s+a_0} $$ 重新排列上述等式為 $$ (s^n+a_{n-1}s^{n-1}+...+a_0)V(s)=U(s) $$ 對兩邊應用拉普拉斯逆變換。 $$ \frac{\text{d}^nv(t)}{\text{d}t^n}+a_{n-1}\frac{\text{d}^{n-1}v(t)}{\text{d}t^{n-1}}+...+a_1 \frac{\text{d}v(t)}{\text{d}t}+a_0v(t)=u(t) $$ 令 $$ v(t)=x_1 $$ $$ \frac{\text{d}v(t)}{\text{d}t}=x_2=\dot{x}_1 $$ $$ \frac{\text{d}^2v(t)}{\text{d}t^2}=x_3=\dot{x}_2 $$ $$.$$ $$.$$ $$.$$ $$ \frac{\text{d}^{n-1}v(t)}{\text{d}t^{n-1}}=x_n=\dot{x}_{n-1} $$ $$ \frac{\text{d}^nv(t)}{\text{d}t^n}=\dot{x}_n $$ 和 u(t) = u 則狀態方程為 $$ \dot{x}_n=-a_0x_1-a_1x_2-...-a_{n-1}x_n+u $$ 考慮: $$ \frac{Y(s)}{V(s)}=b_ns^n+b_{n-1}s^{n-1}+...+b_1s+b_0 $$ 重新排列上述等式為 $$ Y(s)=(b_ns^n+b_{n-1}s^{n-1}+...+b_1s+b_0)V(s) $$ 對兩邊應用拉普拉斯逆變換。 $$ y(t)=b_n\frac{\text{d}^nv(t)}{\text{d}t^n}+b_{n-1}\frac{\text{d}^{n-1}v(t)}{\text{d}t^{n-1}}+...+b_1\frac{\text{d}v(t)}{\text{d}t}+b_0v(t) $$ 將狀態變數和$y(t)=y$代入上述方程,得到輸出方程為: $$ y=b_n\dot{x}_n+b_{n-1}x_n+...+b_1x_2+b_0x_1 $$ 代入$\dot{x}_n$的值到上述方程。 $$ y=b_n(-a_0x_1-a_1x_2-...-a_{n-1}x_n+u)+b_{n-1}x_n+...+b_1x_2+b_0x_1 $$ $$ y=(b_0-b_na_0)x_1+(b_1-b_na_1)x_2+...+(b_{n-1}-b_na_{n-1})x_n+b_n u $$ 狀態空間模型為 $\dot{X} = \begin{bmatrix} \dot{x}_1 \\ \dot{x}_2 \\ \vdots \\ \dot{x}_{n-1} \\ \dot{x}_n \end{bmatrix}$ $$=\begin{bmatrix}0 & 1 & 0 & \cdots & 0 & 0 \\0 & 0 & 1 & \cdots & 0 & 0 \\\vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & 0 & \cdots & 0 & 1 \\-a_0 & -a_1 & -a_2 & \cdots & -a_{n-2} & -a_{n-1} \end{bmatrix} \begin{bmatrix}x_1 \\x_2 \\\vdots \\x_{n-1} \\x_n \end{bmatrix}+\begin{bmatrix}0 \\0 \\\vdots \\0 \\b_0 \end{bmatrix}\begin{bmatrix}u \end{bmatrix}$$ $$ Y=[b_0-b_na_0 \quad b_1-b_na_1 \quad ... \quad b_{n-2}-b_na_{n-2} \quad b_{n-1}-b_na_{n-1}]\begin{bmatrix}x_1 \\x_2 \\\vdots \\x_{n-1} \\x_n \end{bmatrix} $$ 如果$b_n = 0$,則: $$ Y=[b_0 \quad b_1 \quad ...\quad b_{n-2} \quad b_{n-1}]\begin{bmatrix}x_1 \\x_2 \\\vdots \\x_{n-1} \\x_n \end{bmatrix} $$ 在上一章中,我們學習瞭如何從微分方程和傳遞函式獲得狀態空間模型。本章,讓我們討論如何從狀態空間模型獲得傳遞函式。 我們知道線性時不變 (LTI) 系統的狀態空間模型為: $$ \dot{X} = AX + BU $$ $$ Y = CX + DU $$ 對狀態方程的兩邊進行拉普拉斯變換。 $$ sX(s)=AX(s)+BU(s) $$ $$ \Rightarrow (sI-A)X(s)=BU(s) $$ $$ \Rightarrow X(s)=(sI-A)^{-1}BU(s) $$ 對輸出方程的兩邊進行拉普拉斯變換。 $$ Y(s)=CX(s)+DU(s) $$ 代入X(s)的值到上述方程。 $$ \Rightarrow Y(s)=C(sI-A)^{-1}BU(s)+DU(s) $$ $$ \Rightarrow Y(s)=[C(sI-A)^{-1}B+D]U(s) $$ $$ \Rightarrow \frac{Y(s)}{U(s)}=C(sI-A)^{-1}B+D $$ 上述方程表示系統的傳遞函式。因此,我們可以使用此公式計算以狀態空間模型表示的系統的傳遞函式。 注意 − 當$D = [0]$時,傳遞函式為 $$ \frac{Y(s)}{U(s)}=C(sI-A)^{-1}B $$ 示例 讓我們計算以狀態空間模型表示的系統的傳遞函式,如下所示: $$ \dot{X}=\begin{bmatrix}\dot{x}_1 \\\dot{x}_2 \end{bmatrix}=\begin{bmatrix}-1 & -1 \\1 & 0 \end{bmatrix}\begin{bmatrix}x_1 \\x_2 \end{bmatrix}+\begin{bmatrix}1 \\0 \end{bmatrix}[u] $$ $$ Y=\begin{bmatrix}0 & 1 \end{bmatrix}\begin{bmatrix}x_1 \\x_2 \end{bmatrix} $$ 此處, $$ A=\begin{bmatrix}-1 & -1 \\1 & 0 \end{bmatrix}, \quad B=\begin{bmatrix}1 \\0 \end{bmatrix}, \quad C=\begin{bmatrix}0 & 1 \end{bmatrix} \quad and \quad D=[0] $$ 當$D = [0]$時的傳遞函式公式為: $$ \frac{Y(s)}{U(s)}=C(sI-A)^{-1}B $$ 代入A,B和C矩陣到上述方程。 $$ \frac{Y(s)}{U(s)}=\begin{bmatrix}0 & 1 \end{bmatrix}\begin{bmatrix}s+1 & 1 \\-1 & s \end{bmatrix}^{-1}\begin{bmatrix}1 \\0 \end{bmatrix} $$ $$ \Rightarrow \frac{Y(s)}{U(s)}=\begin{bmatrix}0 & 1 \end{bmatrix} \frac{\begin{bmatrix}s & -1 \\1 & s+1 \end{bmatrix}}{(s+1)s-1(-1)}\begin{bmatrix}1 \\0 \end{bmatrix} $$ $$ \Rightarrow \frac{Y(s)}{U(s)}=\frac{\begin{bmatrix}0 & 1 \end{bmatrix}\begin{bmatrix}s \\1 \end{bmatrix}}{s^2+s+1}=\frac{1}{s^2+s+1} $$ 因此,給定狀態空間模型的系統的傳遞函式為 $$ \frac{Y(s)}{U(s)}=\frac{1}{s^2+s+1} $$ 如果系統具有初始條件,則它將產生輸出。由於即使在沒有輸入的情況下也存在此輸出,因此它被稱為零輸入響應$x_{ZIR}(t)$。數學上,我們可以將其寫成: $$ x_{ZIR}(t)=e^{At}X(0)=L^{-1}\left \{ \left [ sI-A \right ]^{-1}X(0) \right \} $$ 從上述關係,我們可以將狀態轉移矩陣$\phi(t)$寫成 $$ \phi(t)=e^{At}=L^{-1}[sI-A]^{-1} $$ 因此,可以透過將狀態轉移矩陣$\phi(t)$與初始條件矩陣相乘來獲得零輸入響應。 以下是狀態轉移矩陣的性質。 如果$t = 0$,則狀態轉移矩陣將等於單位矩陣。 $$ \phi(0) = I $$ 狀態轉移矩陣的逆矩陣與狀態轉移矩陣相同,只是將‘t’替換為‘-t’。 $$ \phi^{-1}(t) = \phi(−t) $$ 如果$t = t_1 + t_2$,則對應的狀態轉移矩陣等於$t = t_1$和$t = t_2$時兩個狀態轉移矩陣的乘積。 $$ \phi(t_1 + t_2) = \phi(t_1) \phi(t_2) $$ 現在讓我們逐一討論控制系統的可控性和可觀測性。 如果控制系統的初始狀態可以透過有限時間內的受控輸入轉移(改變)到一些其他期望狀態,則稱該控制系統是可控的。 我們可以使用卡爾曼檢驗來檢查控制系統的可控性。 以如下形式寫矩陣$Q_c$。 $$ Q_c=\left [ B \quad AB \quad A^2B \quad ...\quad A^{n-1}B \right ] $$ 求矩陣$Q_c$的行列式,如果它不等於零,則控制系統是可控的。 如果能夠透過在有限時間內觀察輸出確定控制系統的初始狀態,則稱該控制系統是可觀測的。 我們可以使用卡爾曼檢驗來檢查控制系統的可觀測性。 以如下形式寫矩陣$Q_o$。 $$ Q_o=\left [ C^T \quad A^TC^T \quad (A^T)^2C^T \quad ...\quad (A^T)^{n-1}C^T \right ] $$ 求矩陣$Q_o$的行列式,如果它不等於零,則控制系統是可觀測的。 示例 讓我們驗證以狀態空間模型表示的控制系統的可控性和可觀測性,如下所示: $$ \dot{x}=\begin{bmatrix}\dot{x}_1 \\\dot{x}_2 \end{bmatrix}=\begin{bmatrix}-1 & -1 \\1 & 0 \end{bmatrix}\begin{bmatrix}x_1 \\x_2 \end{bmatrix}+\begin{bmatrix}1 \\0 \end{bmatrix} [u] $$ $$ Y=\begin{bmatrix}0 & 1 \end{bmatrix}\begin{bmatrix}x_1 \\x_2 \end{bmatrix} $$ 此處, $$ A=\begin{bmatrix}-1 & -1 \\1 & 0 \end{bmatrix}, \quad B=\begin{bmatrix}1 \\0 \end{bmatrix}, \quad \begin{bmatrix}0 & 1 \end{bmatrix}, D=[0]\quad and \quad n=2 $$ 對於$n = 2$,矩陣$Q_c$將為 $$ Q_c=\left [B \quad AB \right ] $$ 我們將得到矩陣A和B的乘積為: $$ AB=\begin{bmatrix}-1 \\1 \end{bmatrix} $$ $$ \Rightarrow Q_c =\begin{bmatrix}1 & -1 \\0 & 1 \end{bmatrix} $$ $$ |Q_c|=1 \neq 0 $$ 由於矩陣$Q_c$的行列式不等於零,因此給定的控制系統是可控的。 對於$n = 2$,矩陣$Q_o$將為: $$ Q_o=\left [C^T \quad A^TC^T \right ] $$ 此處, $$ A^T=\begin{bmatrix}-1 & 1 \\-1 & 0 \end{bmatrix} \quad and \quad C^T=\begin{bmatrix}0 \\1 \end{bmatrix} $$ 我們將得到矩陣$A^T$和$C^T$的乘積為 $$ A^TC^T=\begin{bmatrix}1 \\0 \end{bmatrix} $$ $$ \Rightarrow Q_o=\begin{bmatrix}0 & 1 \\1 & 0 \end{bmatrix} $$ $$ \Rightarrow |Q_o|=-1 \quad \neq 0 $$ 由於矩陣$Q_o$的行列式不等於零,因此給定的控制系統是可觀測的。 因此,給定的控制系統既可控又可觀測。
示例

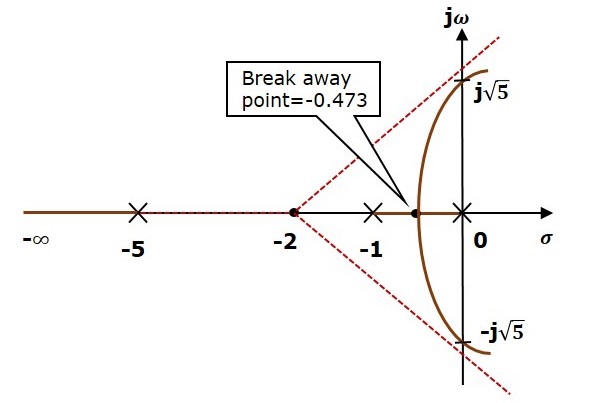
新增開環極點和零點對根軌跡的影響
頻率響應分析
什麼是頻域響應?
頻域指標
諧振頻率
諧振峰值
頻寬
控制系統 - 波特圖
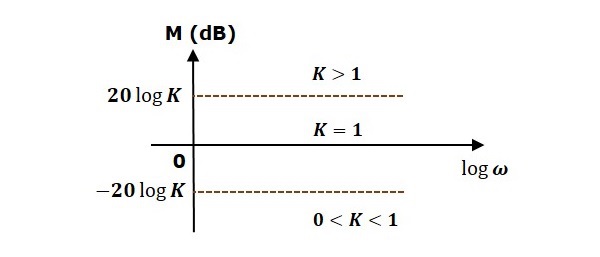
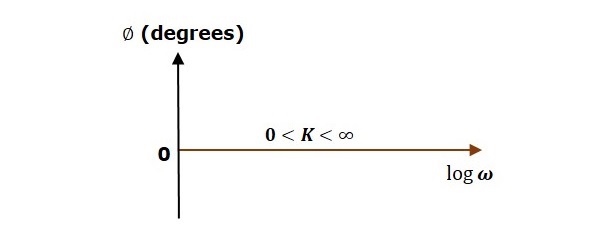
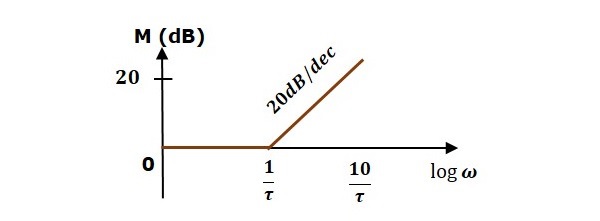
伯德圖基礎
項的型別
G(jω)H(jω)
斜率(dB/dec)
幅值 (dB)
相角(度)



控制系統 - 伯德圖的繪製
伯德圖繪製規則
示例
利用伯德圖進行穩定性分析
相位交越頻率
增益穿越頻率
增益裕度
相位裕度
控制系統 - 極座標圖
繪製極座標圖的規則
示例
頻率 (rad/sec)
幅值
相角(度)
0
0
∞
0
0
-90 或 270
控制系統 - 奈奎斯特圖
奈奎斯特圖是極座標圖的延續,透過將ω從−∞變到∞來確定閉環控制系統的穩定性。這意味著奈奎斯特圖用於繪製開環傳遞函式的完整頻率響應。
奈奎斯特穩定性判據指出,圍繞臨界點(1+j0)的環繞數必須等於特徵方程的極點數,也就是's'平面右半部分開環傳遞函式的極點數。將原點移到(1+j0)得到特徵方程平面。
繪製奈奎斯特圖後,我們可以使用奈奎斯特穩定性判據找到閉環控制系統的穩定性。如果臨界點(-1+j0)位於環繞之外,則閉環控制系統絕對穩定。
相位交越頻率
增益穿越頻率
增益裕度
相位裕度
控制系統 - 校正器
如果增益裕度$GM$小於1和/或相位裕度$PM$為負,則控制系統為不穩定的。
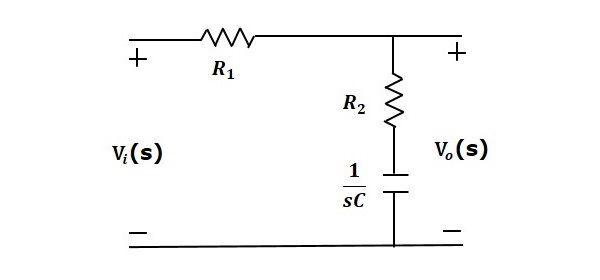
超前補償器

滯後-超前補償器
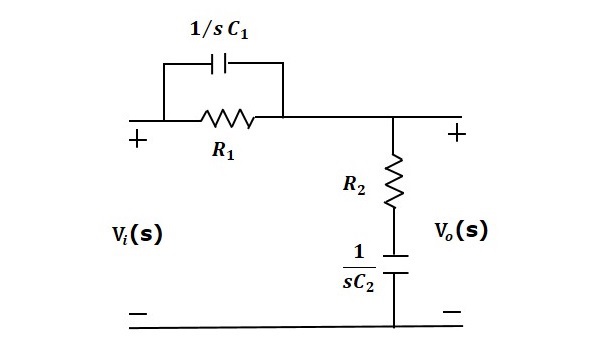
控制系統 - 控制器
比例控制器
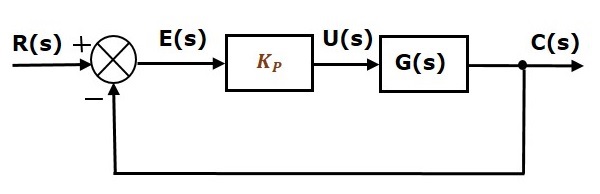
微分控制器
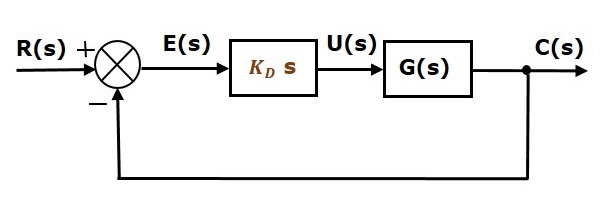
積分控制器
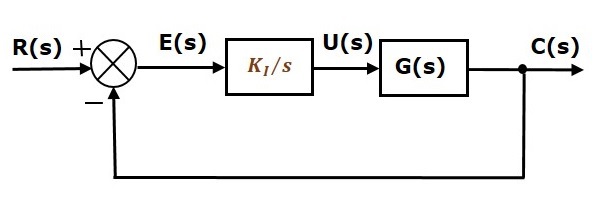
比例微分 (PD) 控制器

比例積分 (PI) 控制器
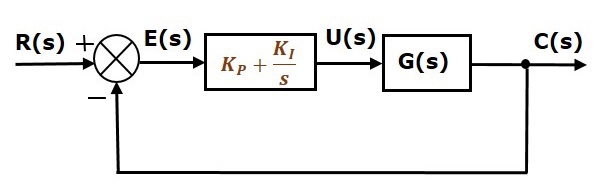
比例積分微分 (PID) 控制器
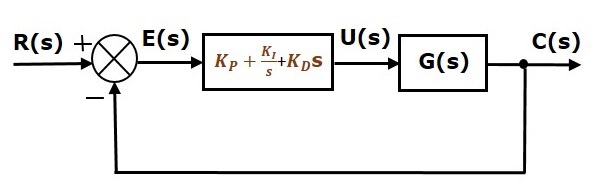
控制系統 - 狀態空間模型
狀態空間模型的基本概念
狀態
狀態變數
狀態向量
從微分方程獲得狀態空間模型

從傳遞函式獲得狀態空間模型
分子中具有常數項的傳遞函式
示例
分子為s的多項式函式的傳遞函式
控制系統 - 狀態空間分析
從狀態空間模型獲得傳遞函式
狀態轉移矩陣及其性質
可控性和可觀測性
可控性
可觀測性
