根軌跡繪製

---

---

根軌跡是s域中的圖形表示，它關於實軸對稱。因為開環極點和零點存在於s域中，其值可以是實數或複共軛對。本章我們將討論如何繪製根軌跡。

根軌跡繪製規則

遵循以下規則繪製根軌跡：

規則1 − 在‘s’平面上定位開環極點和零點。

規則2 − 確定根軌跡分支的數量。

我們知道，根軌跡分支始於開環極點，終止於開環零點。因此，根軌跡分支數N等於有限開環極點數P或有限開環零點數Z中的較大者。

數學上，我們可以將根軌跡分支數N寫為

$N=P$ 如果 $P\geq Z$

$N=Z$ 如果 $P<Z$

規則3 − 識別並繪製實軸根軌跡分支。

如果在某一點上開環傳遞函式的相位角為180⁰的奇數倍，則該點位於根軌跡上。如果在實軸上某點左側存在奇數個開環極點和零點，則該點位於根軌跡分支上。因此，滿足此條件的點分支為根軌跡分支的實軸。

規則4 − 尋找漸近線的中心和角度。

• 如果 $P = Z$，則所有根軌跡分支都從有限開環極點開始，並在有限開環零點結束。

• 如果 $P > Z$，則 $Z$ 個根軌跡分支從有限開環極點開始，並在有限開環零點結束；而 $P − Z$ 個根軌跡分支從有限開環極點開始，並在無限開環零點結束。

• 如果 $P < Z$，則P個根軌跡分支從有限開環極點開始，並在有限開環零點結束；而 $Z − P$ 個根軌跡分支從無限開環極點開始，並在有限開環零點結束。

因此，當 $P \neq Z$ 時，一些根軌跡分支趨於無窮大。漸近線給出了這些根軌跡分支的方向。漸近線在實軸上的交點稱為中心。

我們可以使用以下公式計算中心 α：

$\alpha = \frac{\sum 有限開環極點的實部\:-\sum 有限開環零點的實部}{P-Z}$

漸近線角度 θ的公式為

$$\theta=\frac{(2q+1)180^0}{P-Z}$$

其中，

$$q=0,1,2,....,(P-Z)-1$$

規則5 − 尋找根軌跡分支與虛軸的交點。

我們可以使用勞斯陣列法和特殊情況(ii)計算根軌跡分支與虛軸的交點以及該點的K值。

• 如果勞斯陣列的任何一行的所有元素都為零，則根軌跡分支與虛軸相交，反之亦然。

• 找到這樣的一行，如果我們將第一個元素設為零，則該行的所有元素都為零。找到此組合的K值。

• 將此K值代入輔助方程。您將得到根軌跡分支與虛軸的交點。

規則6 − 尋找分離點和匯合點。

• 如果在兩個開環極點之間存在實軸根軌跡分支，則這兩個開環極點之間將存在一個分離點。

• 如果在兩個開環零點之間存在實軸根軌跡分支，則這兩個開環零點之間將存在一個匯合點。

注意 − 分離點和匯合點僅存在於實軸根軌跡分支上。

按照以下步驟查詢分離點和匯合點：

• 從特徵方程 $1 + G(s)H(s) = 0$ 中寫出關於 $s$ 的 $K$。

• 對 $K$ 關於 $s$ 求導，並使其等於零。將這些 $s$ 值代入上述方程。

• $K$ 值為正的 $s$ 值是分離點。

規則7 − 尋找起始角和到達角。

分別可以在複共軛開環極點和複共軛開環零點處計算起始角和到達角。

起始角 $\phi_d$ 的公式為

$$\phi_d=180^0-\phi$$

到達角 $\phi_a$ 的公式為

$$\phi_a=180^0+\phi$$

其中，

$$\phi=\sum \phi_P-\sum \phi_Z$$

示例

現在讓我們繪製具有開環傳遞函式 $G(s)H(s)=\frac{K}{s(s+1)(s+5)}$ 的控制系統的根軌跡。

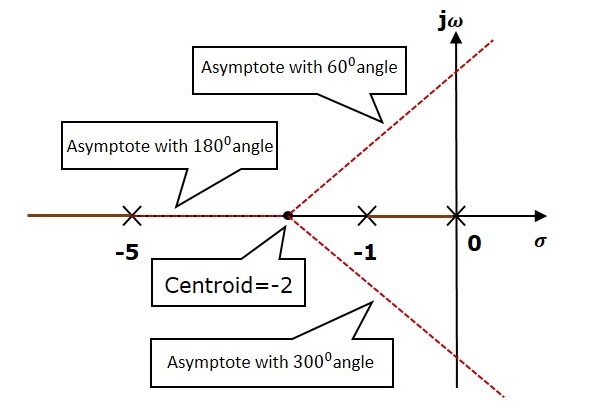
步驟1 − 給定的開環傳遞函式在 $s = 0, s = −1$ 和 $s = −5$ 處有三個極點。它沒有任何零點。因此，根軌跡分支的數量等於開環傳遞函式的極點數。

$$N=P=3$$

三個極點的位置如上圖所示。$s = −1$ 和 $s = 0$ 之間的線段是實軸上根軌跡的一個分支。實軸上根軌跡的另一個分支是 $s = −5$ 左側的線段。

步驟2 − 我們將使用給定的公式得到中心和漸近線的角度值。

中心 $\alpha = −2$

漸近線的角度為 $\theta = 60^0,180^0$ 和 $300^0$。

中心和三條漸近線如下圖所示。

步驟3 − 由於兩條漸近線的角度為 $60^0$ 和 $300^0$，因此兩個根軌跡分支與虛軸相交。透過使用勞斯陣列法和特殊情況(ii)，根軌跡分支與虛軸在 $j\sqrt{5}$ 和 $−j\sqrt{5}$ 處相交。

在極點 $s = −1$ 和 $s = 0$ 之間的實軸根軌跡分支上將存在一個分離點。按照給定的計算分離點的步驟，我們將得到 $s = −0.473$。

給定控制系統的根軌跡圖如下圖所示。

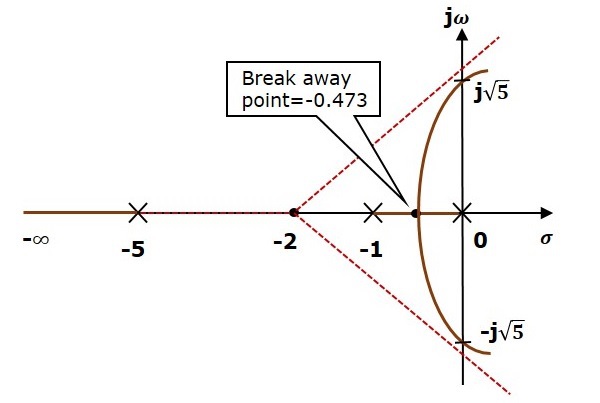
透過這種方式，您可以繪製任何控制系統的根軌跡圖，並觀察閉環傳遞函式極點的移動。

從根軌跡圖中，我們可以知道不同型別阻尼的K值範圍。

新增開環極點和零點對根軌跡的影響

透過新增開環極點和開環零點，可以將根軌跡在‘s’平面上移動。

• 如果我們在開環傳遞函式中包含一個極點，則一些根軌跡分支將移向‘s’平面的右半平面。因此，阻尼比 $\delta$ 減小。這意味著阻尼頻率 $\omega_d$ 增加，時域指標如延遲時間 $t_d$、上升時間 $t_r$ 和峰值時間 $t_p$ 減小。但是，它會影響系統穩定性。

• 如果我們在開環傳遞函式中包含一個零點，則一些根軌跡分支將移向‘s’平面的左半平面。因此，它將提高控制系統的穩定性。在這種情況下，阻尼比 $\delta$ 增加。這意味著阻尼頻率 $\omega_d$ 減小，時域指標如延遲時間 $t_d$、上升時間 $t_r$ 和峰值時間 $t_p$ 增加。

因此，根據要求，我們可以將開環極點或零點包含（新增到）傳遞函式中。