控制系統 - 方框圖代數

---

---

方框圖代數只不過是方框圖基本元素相關的代數運算。這種代數處理的是代數方程的圖形表示。

方框的基本連線

兩個方框之間有三種基本型別的連線。

串聯連線

串聯連線也稱為級聯連線。在下圖中，兩個具有傳遞函式$G_1(s)$和$G_2(s)$的方框串聯連線。

對於這種組合，我們將得到輸出$Y(s)$為

$$Y(s)=G_2(s)Z(s)$$

其中，$Z(s)=G_1(s)X(s)$

$$\Rightarrow Y(s)=G_2(s)[G_1(s)X(s)]=G_1(s)G_2(s)X(s)$$

$$\Rightarrow Y(s)=\lbrace G_1(s)G_2(s)\rbrace X(s)$$

將此方程與輸出方程的標準形式$Y(s)=G(s)X(s)$進行比較。其中，$G(s) = G_1(s)G_2(s)$。

這意味著我們可以用一個方框表示兩個方框的串聯連線。這個單一方框的傳遞函式是這兩個方框的傳遞函式的乘積。等效方框圖如下所示。

類似地，您可以用一個方框表示'n'個方框的串聯連線。這個單一方框的傳遞函式是所有這'n'個方框的傳遞函式的乘積。

並聯連線

並聯連線的方框將具有相同的輸入。在下圖中，兩個具有傳遞函式$G_1(s)$和$G_2(s)$的方框並聯連線。這兩個方框的輸出連線到求和點。

對於這種組合，我們將得到輸出$Y(s)$為

$$Y(s)=Y_1(s)+Y_2(s)$$

其中，$Y_1(s)=G_1(s)X(s)$和$Y_2(s)=G_2(s)X(s)$

$$\Rightarrow Y(s)=G_1(s)X(s)+G_2(s)X(s)=\lbrace G_1(s)+G_2(s)\rbrace X(s)$$

將此方程與輸出方程的標準形式$Y(s)=G(s)X(s)$進行比較。

其中，$G(s)=G_1(s)+G_2(s)$。

這意味著我們可以用一個方框表示兩個方框的並聯連線。這個單一方框的傳遞函式是這兩個方框的傳遞函式的和。等效方框圖如下所示。

類似地，您可以用一個方框表示'n'個方框的並聯連線。這個單一方框的傳遞函式是所有這'n'個方框的傳遞函式的代數和。

反饋連線

正如我們在前幾章中討論的那樣，有兩種型別的反饋——正反饋和負反饋。下圖顯示了負反饋控制系統。在這裡，兩個具有傳遞函式$G(s)$和$H(s)$的方框形成一個閉環。

求和點的輸出是：

$$E(s)=X(s)-H(s)Y(s)$$

輸出$Y(s)$是：

$$Y(s)=E(s)G(s)$$

將$E(s)$的值代入上述方程。

$$Y(s)=\left \{ X(s)-H(s)Y(s)\rbrace G(s) \right\}$$

$$Y(s)\left \{ 1+G(s)H(s)\rbrace = X(s)G(s) \right\}$$

$$\Rightarrow \frac{Y(s)}{X(s)}=\frac{G(s)}{1+G(s)H(s)}$$

因此，負反饋閉環傳遞函式為$\frac{G(s)}{1+G(s)H(s)}$

這意味著我們可以用一個方框表示兩個方框的負反饋連線。這個單一方框的傳遞函式是負反饋的閉環傳遞函式。等效方框圖如下所示。

類似地，您可以用一個方框表示兩個方框的正反饋連線。這個單一方框的傳遞函式是正反饋的閉環傳遞函式，即$\frac{G(s)}{1-G(s)H(s)}$

求和點的方框圖代數

相對於方框，移動求和點有兩種可能性：

• 將求和點移到方框之後
• 將求和點移到方框之前

現在讓我們逐一看看上述兩種情況下需要進行什麼樣的安排。

將求和點移到方框之後

考慮下圖所示的方框圖。在這裡，求和點位於方框之前。

求和點有兩個輸入$R(s)$和$X(s)$。它的輸出是$\left \{R(s)+X(s)\right\}$。

因此，方框$G(s)$的輸入是$\left \{R(s)+X(s)\right \}$，其輸出為：

$$Y(s)=G(s)\left \{R(s)+X(s)\right \}$$

$\Rightarrow Y(s)=G(s)R(s)+G(s)X(s)$ (公式1)

現在，將求和點移到方框之後。此方框圖如下圖所示。

方框$G(s)$的輸出是$G(s)R(s)$。

求和點的輸出是

$Y(s)=G(s)R(s)+X(s)$ (公式2)

比較公式1和公式2。

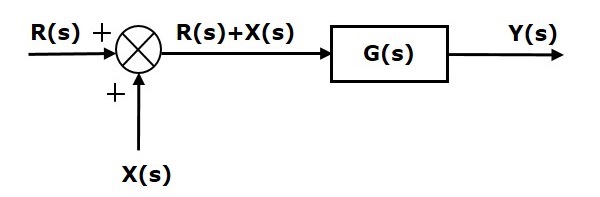
第一項$‘G(s) R(s)’$在兩個方程中都是相同的。但是，第二項有所不同。為了使第二項也相同，我們需要另一個方框$G(s)$。它具有輸入$X(s)$，並且此方框的輸出作為輸入提供給求和點，而不是$X(s)$。此方框圖如下圖所示。

將求和點移到方框之前

考慮下圖所示的方框圖。在這裡，求和點位於方框之後。

此方框圖的輸出為：

$Y(s)=G(s)R(s)+X(s)$ (公式3)

現在，將求和點移到方框之前。此方框圖如下圖所示。

此方框圖的輸出為：

$Y(S)=G(s)R(s)+G(s)X(s)$ (公式4)

比較公式3和公式4，

第一項$‘G(s) R(s)’$在兩個方程中都是相同的。但是，第二項有所不同。為了使第二項也相同，我們需要另一個方框$\frac{1}{G(s)}$。它具有輸入$X(s)$，並且此方框的輸出作為輸入提供給求和點，而不是$X(s)$。此方框圖如下圖所示。

取樣點的方框圖代數

相對於方框，移動取樣點有兩種可能性：

• 將取樣點移到方框之後
• 將取樣點移到方框之前

現在讓我們逐一看看上述兩種情況下需要進行什麼樣的安排。

將取樣點移到方框之後

考慮下圖所示的方框圖。在這種情況下，取樣點位於方框之前。

這裡，$X(s)=R(s)$和$Y(s)=G(s)R(s)$

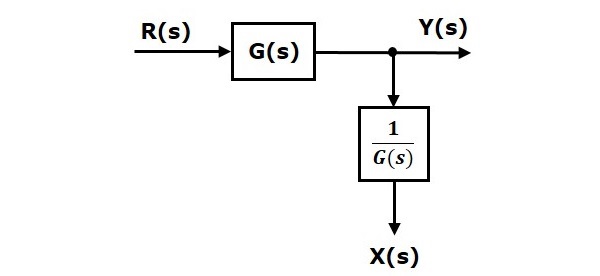
當您將取樣點移到方框之後時，輸出$Y(s)$將保持不變。但是，$X(s)$的值有所不同。因此，為了獲得相同的$X(s)$值，我們需要另一個方框$\frac{1}{G(s)}$。它具有輸入$Y(s)$，輸出為$X(s)$。此方框圖如下圖所示。

將取樣點移到方框之前

考慮下圖所示的方框圖。在這裡，取樣點位於方框之後。

這裡，$X(s)=Y(s)=G(s)R(s)$

當您將取樣點移到方框之前時，輸出$Y(s)$將保持不變。但是，$X(s)$的值有所不同。因此，為了獲得相同的$X(s)$值，我們需要另一個方框$G(s)$。它具有輸入$R(s)$，輸出為$X(s)$。此方框圖如下圖所示。